
- •7.7 Рекомендуемая литература Основная
- •Дополнительная
- •8 Четырехполюсники и цепочечные lc-фильтры
- •8.1 Цель занятия по теме "Четырехполюсники"
- •8.2 Основные положения теории четырехполюсников
- •8.2.1 Определение и типы параметров
- •8.2.2 Внутренние параметры
- •8.2.3 Характеристические параметры
- •Для электрически симметричного четырехполюсника
- •8.2.4 Рабочие параметры
- •8.2.5 Схемные функции
- •8.3 Примеры решения задач
- •8.4 Задачи для самостоятельной работы
- •8.5 Цель занятия по теме “Цепочечные lc-фильтры”
- •8.6. Основные положения теории цепочечных
8.2.4 Рабочие параметры
Рабочая
постоянная передачи
![]() определяется для произвольно нагруженного
четырехполюсника
определяется для произвольно нагруженного
четырехполюсника
 (8.16)
(8.16)
где
![]() - напряжение и ток на выходе произвольно
нагруженного четырехполюсника,
работающего от генератора с внутренним
сопротивлением
- напряжение и ток на выходе произвольно
нагруженного четырехполюсника,
работающего от генератора с внутренним
сопротивлением
![]() и э.д.с.
и э.д.с.
![]() ,
,
![]() -
напряжение и ток на полностью согласованной
нагрузке, подключенной непосредственно
к прежнему генератору в соответствии
с рисунком 8.4.
-
напряжение и ток на полностью согласованной
нагрузке, подключенной непосредственно
к прежнему генератору в соответствии
с рисунком 8.4.

8.2.5 Схемные функции
Схемные
функции произвольно нагруженного
четырехполюсника
![]() и
и
![]() в общем случае) (рисунок 8.5.) могут быть
выражены через любые первичные параметры,
в общем случае) (рисунок 8.5.) могут быть
выражены через любые первичные параметры,

например,
![]() (8.17)
(8.17)
![]() (8.18)
(8.18)
 (8.19)
(8.19)
где
![]() а
а
![]() -
определитель матрицы Y - параметров.
-
определитель матрицы Y - параметров.
При
определении
![]() вых
источник
вых
источник
![]() помещается последовательно с
помещается последовательно с
![]() а
выводы 1-1
соединяются через Zi
а
выводы 1-1
соединяются через Zi
вых
=
![]() (8.20)
(8.20)
где
![]()
Схемные функции могут быть выражены через любые другие параметры с помощью таблицы 8.1.
8.3 Примеры решения задач
Задача 1. Для заданного четырехполюсника (рисунок 8.6) определить А-параметры.

Решение.
Вариант 1. В соответствии с общей методикой поочередного устранения пары искомых параметров из системы А-параметров следует
 т.к.
на Z1
нет падения напряжения;
т.к.
на Z1
нет падения напряжения;
 т.к.
т.к.
![]() ;
;
 т.к.
т.к.
![]()
 т.к.
т.к.
![]() при к.з. на выходе.
при к.з. на выходе.
В
матричной форме
![]() .
.
Проверка: А= 1, что соответствует пассивным цепям.
Вариант 2. Определим Y - параметры через матрицу проводимостей по методу узловых потенциалов, т.к. схема содержит два узла, кроме общего, опорного
 .
.
Перейдём к А-параметрам в соответствии с таблицей 8.1
![]()
![]() ,
,
![]() т.к.
Y
= 0 ;
т.к.
Y
= 0 ;
![]() .
.
Оба варианта дают одинаковый результат.
Задача 2. Определить А- и Y-параметры для четырехполюсника на рисунке 8.7а.

Решение.
В соответствии с общей методикой, как это сделано в первом варианте в задаче 1, по схеме рисунка 8.7.а (х.х. на выходе):
![]()
по схеме рисунка 8.7.б (к.з. на выходе):


А22 можно было определить из условия А = 1 при известных остальных параметрах.
Для определения Y-параметров можно воспользоваться общей методикой

что соответствует схеме 8.8.а;

что соответствует схеме 8.8.б.

Для определения Y-параметров можно воспользоваться формулами перехода от А-параметров к Y-параметрам в таблице 8.1. И. наконец, т.к. в схеме (рисунок 8.7.а) только два узла, кроме опорного, проще всего определить Y-параметры через матрицу проводимостей по методу узловых потенциалов
 .
.
Задача 3. Определить А-параметры Т-образной схемы на рисунке 8.9

Решение.
Т.к. заданную схему можно рассматривать как каскадное соединение двух четырехполюсников с известными параметрами, то в соответствии с соотношениями из таблицы 8.2


Обратите
внимание, что в случае симметричной
схемы на рисунке 8.9, т.е.
![]() и независимо от симметрии А
= 1.
и независимо от симметрии А
= 1.
Задача
4. Найти
коэффициент передачи
![]() для схемы рисунка 8.9, нагруженной на
сопротивление
для схемы рисунка 8.9, нагруженной на
сопротивление
![]() при условии, что
при условии, что
![]() .
Получить такое же выражение
одним из нижеперечисленных способов:
по методу контурных токов, по методу
узловых потенциалов, по методу
эквивалентного генератора, с использованием
эквивалентных преобразований.
.
Получить такое же выражение
одним из нижеперечисленных способов:
по методу контурных токов, по методу
узловых потенциалов, по методу
эквивалентного генератора, с использованием
эквивалентных преобразований.
Решение.
В соответствии с выражением (8.17)
![]() .
.
В
задаче 3 были определены А-параметры
Т-образной схемы; с учетом
![]()
![]() ,
,
![]()

Получим
![]() последним из заданных способов. Схему
рисунка 8.10а представим в виде схемы на
рисунке 8.10б.
последним из заданных способов. Схему
рисунка 8.10а представим в виде схемы на
рисунке 8.10б.

 ,
,
![]() ,
,
 ,
,

Итоговые
выражения
,
его АЧХ и ФЧХ зависят от конкретного
содержания двухполюсников
![]() и
и
![]()
Например,
для частного случая
![]()
![]() ,
,
![]() ,
,
![]() .
.
Примечание: 1) для типовых схем (Г-, Т-, П-образных и ряда других) значения первичных параметров табулированы, что существенно упрощает расчеты схемных функций достаточно сложных цепей, если они могут быть представлены известными соединениями таких четырехполюсников;
2) преимущества теории четырехполюсников невозможно оценить в процессе решения задач для простых схем; некоторое представление о преимуществах использования теории четырехполюсников дает следующая задача.
Задача
5. Транзистор
описывается известными Н-параметрами.
Оценить влияние обратной связи при
известном значении
![]() на функции коэффициента передачи
и входного сопротивления
на функции коэффициента передачи
и входного сопротивления
![]() (рисунок 8.11).
(рисунок 8.11).

Решение.
Схему рисунка 8.11 можно рассматривать как параллельное соединение четырехполюсника транзистора и четырехполюсника обратной связи (рисунок 8.12).

Основные этапы решения:
1) от Н-параметров транзистора по соотношениям таблицы 8.1 перейти к Y-параметрам, т.к. соединение параллельное

2) записать Y-параметры для четырехполюсника обратной связи
![]()
3) найти Y-параметры полной схемы как
![]()
4)
записать
![]() для нагруженного транзистора без
обратной связи и
нагруженного четырехполюсника с обратной
связью.
для нагруженного транзистора без
обратной связи и
нагруженного четырехполюсника с обратной
связью.
В соответствии с выражением (8.17)
![]() ,
,
![]()
5)
аналогичным образом записать
![]() и
и
![]() всей схемы в соответствии с выражением
(8.18);
всей схемы в соответствии с выражением
(8.18);
6) используя заданные значения для транзистора и цепи обратной связи, сделать вывод о влиянии обратной связи.
Задача
6. На
некоторой частоте 1
параметры четырехполюсника (рисунок
8.13.а) заданы в омах. Вычислить
характеристические сопротивления
![]() и
и
![]() .
.

Решение.
Вариант 1 - по выражению (8.3).
Для
![]() :
:
![]() =j20,
=j20,
![]() =20+j20,
=20+j20,
![]()
![]() Ом.
Ом.
Для
:
![]() =
=
![]()
![]() =20,
=20,
![]() Ом
.
Ом
.
Вариант 2 - по выражениям (8.4) .
Найти А-параметры для Г-образной модели рисунка 8.13.б

где
![]() Ом,
Ом,
![]() = 20 Ом.
= 20 Ом.
![]() Ом.
Ом.
![]() Ом.
Ом.
Задача
7. Вычислить
![]() и
и
![]() для четырехполюсника (рисунок 8.13.а)
тремя способами. Исходные данные как в
задаче 6.
для четырехполюсника (рисунок 8.13.а)
тремя способами. Исходные данные как в
задаче 6.
Решение.
Вариант
1. Определим
![]() на основе выражения (8.6)
на основе выражения (8.6)

где
![]() в режиме полного согласования (рисунок
8.14)
в режиме полного согласования (рисунок
8.14)

![]() где
где

Значения
Ом и
![]() Ом
определены в задаче 6.
Ом
определены в задаче 6.
![]() Ом,
Ом,
![]() ,
,
 ,
,
![]() ,
,
![]() =0,466,
-bС
= -32046.
=0,466,
-bС
= -32046.
=0,695неп 6 дБ, bС = 32048.
Вариант 2. Определим на основе выражений (8.15).
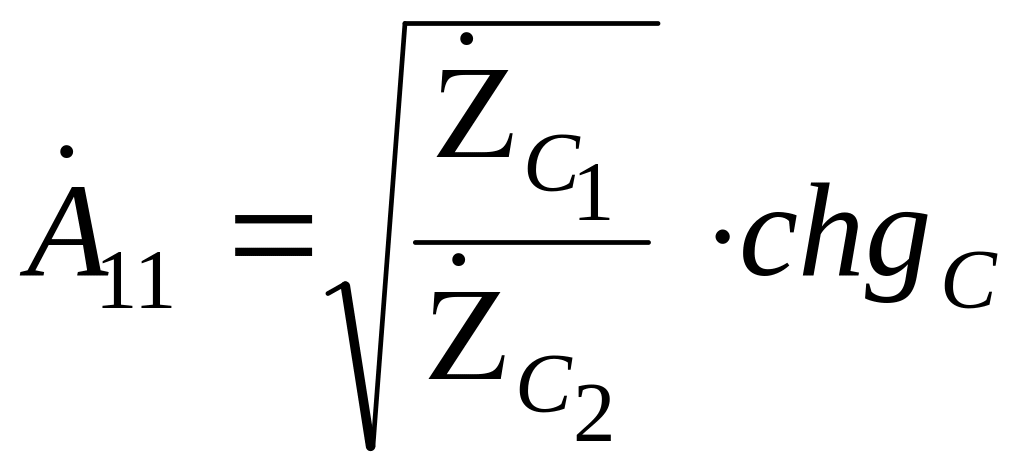 ,
где
,
где
![]() для схемы 8.13а.
для схемы 8.13а.
![]() ;
;
 -
определено выше;
-
определено выше;

откуда
![]()
![]()
= 0,695 неп, bС = 32048.
Примечание:
![]()
если
![]() то
то
![]()
Вариант
3. Определим
![]() на основе выражения (8.14) .
на основе выражения (8.14) .
А-параметры
для схемы рисунка 8.13а при
![]() Ом,
Ом,
![]() =
20 Ом
=
20 Ом
 ,
,
![]()
![]() 2,141,
=
0,695 неп,
2,141,
=
0,695 неп,
![]() =
32049.
=
32049.
