Свойства бинарных отношений

1. Отношение R в множестве М называется рефлексивным , если для справедливо

В матрице смежности на главной диагонали стоят единицы.

В графе каждый элемент (вершина) имеет петлю – дугу вида (т,т):

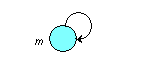
2. Если для справедливо , то отношение R называется антирефлексивным.

В матрице смежности на главной диагонали стоят нули.

В графе нет ни одной петли.

3. Отношение R в множестве М называется симметричным, если для из условия следует , .

Матрица смежности симметрична относительно главной диагонали.

В графе любая пара вершин связана двумя противоположно направленными дугами:

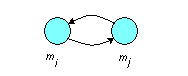
4. Отношение R в множестве М называется антисимметричным, если для из условий и следует, что m_i = m_j или оба отношения и выполняются одновременно только тогда, когда т_i = m_j .

Матрица смежности несимметрична.

В графе могут быть петли, но связь между вершинами, если она имеется, отображается только одной дугой.

5. Отношение R в множестве М называется асимметричным (несимметричным), если для и взаимоисключаются, т.е. если , то и наоборот.

Матрица смежности несимметрична с нулевыми элементами на главной диагонали.

В графе петли отсутствуют, а вершины могут быть связаны только одной дугой.

Если отношение асимметрично, то оно и антирефлексивно.

6. Отношение R в множестве М называется транзитивным , если для из условий и следует, что .

В графе для всякой пары дуг таких, что конец первой совпадает с началом второй, существует третья дуга, имеющая общее начало с первой и общий конец со второй дугой. Эта дуга называется транзитивно замыкающей дугой:

§ 5. Бинарное отношение эквивалентности

Понятия “отношение эквивалентности”, “фактор–множество“, “классы эквивалентности” используются при построении математической модели некоторой реально функционирующей сложной системы. С формальной точки зрения модель есть некоторое фактор – множество элементов моделируемого объекта относительно некоторого отношения эквивалентности, заданного на исходной системе. При исследовании возникает задача выбора существенных свойств, деталей, признаков моделируемого объекта. Отношение эквивалентности, с одной стороны, отождествляет второстепенные, несущественные признаки и свойства, и, с другой – выделяет в качестве представителей классов эквивалентности основные свойства. Если моделируемый объект представлен в виде композиции элементов некоторого базисного множества, то вопрос о соотношении модели и ее прообраза разрешается на основе информации об элементах, на которых вводится отношение эквивалентности – либо это сами элементы базисного множества, либо некоторые подмножества элементов, либо подмножества множества подмножеств элементов.

Бинарное отношение R в множестве М , обладающее свойствами рефлексивности, симметричности и транзитивности, называется отношением эквивалентности и обозначается ~ , то есть для имеет место:

1. каждый элемент эквивалентен сам себе: x ~ x ;

2. если х эквивалентен у, то и у эквивалентен х: если х ~ у, то у ~ х;

3. если х эквивалентен у, а у эквивалентен z , то х эквивалентен z: если х ~ у, а у ~ z , то х ~ z .

Отношение эквивалентности иллюстрируется графом с петлями, каждая пара вершин связана двумя противоположно направленными дугами , которые образуют транзитивно замыкающие дуги :

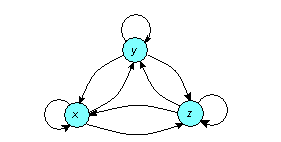
Классом эквивалентности К (т) элемента т называют множество всех элементов m_i , каждый из которых находится с этим элементом в отношении эквивалентности, т.е.

K (m) = {m_i / m_i ~ m}.

Разбиением множества М называется семейство непустых попарно непересекающихся подмножеств (классов), объединение которых совпадает с М .

Проиллюстрируем процедуру построения разбиения множеств.

Пусть на множестве М задано отношение эквивалентности R . Осуществим следующее построение:

- выберем элемент т₁ и образуем подмножество (класс эквивалентности), состоящий из элемента т₁ и всех элементов, эквивалентных т₁ : К (т₁) ;

- выберем элемент , и образуем подмножество (класс эквивалентности) элемента т₂ : К (т₂) , состоящий из элемента т₂ и всех элементов, эквивалентных ему , и т.д. В результате такого построения получится система классов эквивалентности К (т₁), К (т₂), … (возможно бесконечная) такая, что любой элемент из множества М входит хотя бы в один класс, т.е. .

Данная система обладает следующими свойствами:

1. классы эквивалентности попарно не пересекаются:

Ø;

2. любые два элемента из одного класса эквивалентны;

3. любые два элемента из разных классов неэквивалентны.

Построенное разбиение (система классов) называется системой классов эквивалентности по отношению R .

Если бинарное отношение является бинарным отношением эквивалентности, то его матрицу смежности можно привести с помощью перестановок строк (столбцов) к виду

С= .

Здесь около главной диагонали расположены подматрицы, состоящие из единиц, остальные элементы матрицы равны нулю. Каждая подматрица соответствует классу эквивалентности.