§ 6. Метод производящих функций
Метод производящих функций – один из самых развитых теоретических методов комбинаторного анализа и один из самых сильных в приложениях.
Рассмотрим произведение конечного числа линейных биномов
=
.
В правой части равенства коэффициенты имеют вид
.
Действительно, пусть п = 2, тогда
+
.
Аналогично для п
> 2. В частном случае, если
,
в качестве коэффициента
получим числа k-сочетаний,
т.е.
.
(1)
Здесь функция
и числа
связаны взаимно однозначно.
Производящей
функцией
последовательности
называется сумма степенного ряда
.
В нашем случае
функция
является производящей функцией
последовательности
,
т.к.
=
.
С производящей функцией удобно и просто работать. Она “производит” необходимую информацию о последовательности r-сочетаний.
Суть метода
производящих функций: требуется вычислить
все члены некоторой последовательности
.
С помощью рекуррентного соотношения
для
или непосредственно из некоторых
комбинаторных соображений вычисляют
производящую функцию
.
Раскладывая затем
в ряд и находят коэффициенты при
,
тем самым находят
.
Итак из формулы (1) следует, что последовательность биномиальных коэффициентов имеет производящую функцию , т.е.
.
(2)
Пусть
=
,
k
= 0, 1, 2,… Тогда
1 +
= 1 +
.
Полученная
последовательность является бесконечно
убывающей геометрической последовательностью
со знаменателем
при
.
Следовательно, полученный ряд сходится
и его сумма равна
.
Таким образом,
при
.
(3)
Рассмотрим формулу
бинома Ньютона для действительного
показателя
.
Пусть
и
.
Тогда
1 +
,
т.е.
.
(4)
Пусть
и
.
Тогда
.
Но п
=
,
=
,
… ,
=
и т.д. Тогда
.
Таким образом,
.
(5)
Пусть
=
Найдем производящую функцию
для последовательности
с указанными членами.
=
=
=
=
=
=
.
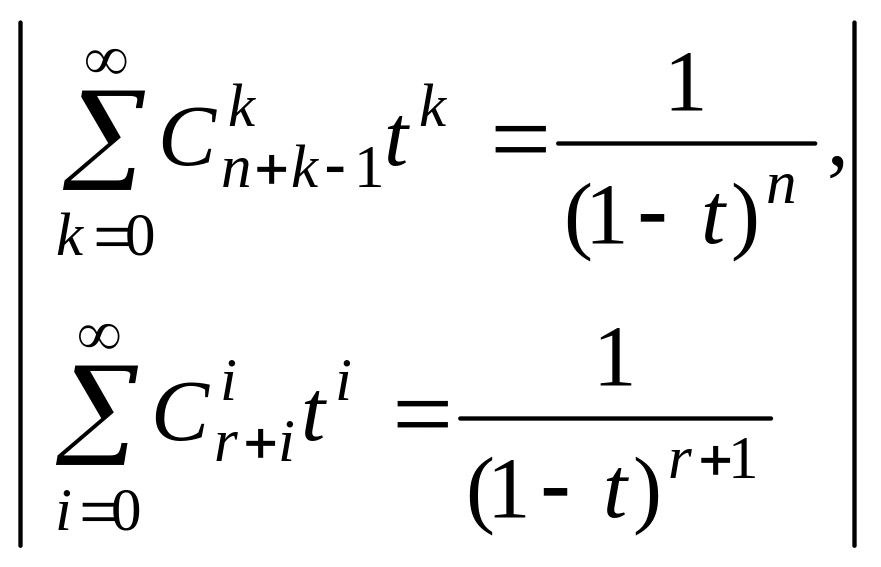Следовательно, производящая функция для заданной последовательности имеет вид
= .
Обобщая, приведем часто встречающиеся производящие функции:
;
;
;
;
;
;
;
.
В комбинаторном анализе чаще всего используются три вида производящих функций: обычные степенные, экспоненциальные, функции Дирихле.
Производящие функции (2) – (5) относятся к обычным производящим функциям. Обычные производящие функции, представляемые в виде , соответствуют семействам последовательностей, элементы которых являются числами неупорядоченных (п, k)-выборок или функциями от них.
Рассмотрим некоторые
операции в классе производящих функций.
Пусть
− класс производящих функций
.
1. Суммой
последовательностей
и
называют последовательность
,
а суммой
производящих
функций
и
− производящую функцию
.
2. Произведением
(сверткой)
последовательностей
и
называют последовательность
,
у которой
,
,
а произведением
(сверткой) производящих функций
и
−
производящую функцию
.
Коэффициенты
получаются при перемножении рядов
следующим образом:
(6)
3. Нуль в классе
производящих функций
− это
=
0; ей соответствует нулевая последовательность
.
4. Единица в классе
производящих функций
− это
=
1; ей соответствует единичная
последовательность
= е.
5. Обратный
относительно сложения (противоположный)
элемент в классе производящих функций
есть функция:
=
=
,
которой соответствует последовательность
.
Обратный элемент
относительно умножения в классе
производящих функций есть функция
=
,
ей соответствует последовательность
,
причем
.
В этом случае, учитывая (6), получим
систему
Здесь число
неизвестных
равно числу уравнений.
6. Умножение
производящей функции на действительное
число
:
.
Производящая функция для (п, r)-сочетаний с ограниченным числом повторений.
В данном случае
для получения производящей функции
нельзя воспользоваться формулой
=
,
т.к. всякий такой бином отражает лишь
две возможности: элемент
множества либо не появляется в
r-сочетаниях,
либо появляется ровно один раз. Пусть
элемент
появляется в r-сочетаниях
с повторениями 0, 1, 2,…, j
раз.. Тогда точно i
появлениям
элемента
будет соответствовать одночлен
,
а по правилу суммы появлению элемента
либо 0, либо 1, … , либо j
раз должен соответствовать многочлен
1 +
… +
.
Тогда производящая функция будет иметь
вид
.
(7)
Если требуется
найти лишь числа
соответствующих (п,
r)-сочетаний,
то необходимо положить
и
=
.
(8)
Коэффициенты здесь будут равны числу сочетаний из п элементов по k с j повторениями.
Пример. □ Рассмотрим сочетания из трех предметов 1, 2, 3; причем 1 и 2 могут встречаться не более двух раз, а 3 – не более одного раза.
Составим производящую функцию по формуле (7):
=
1 +
+
+
+
.
Если
,
то получим
1+
+
.
Здесь коэффициент
равен числу сочетаний из трех по одному
элементу не более чем с двумя повторениями,
− из трех элементов по два не более чем
с двумя повторениями,
− из трех по три элемента с ограничениями,
что первый и второй элементы могут
встречаться не более двух раз, третий
не более одного раза. Если же не
приравнивать
,
то, например, коэффициент при
,
равный
,
показывает “качественный” состав
r-сочетаний
с указанием повторений: 112, 113, 122, 123, 223.
Аналогично коэффициент при
показывает число r-сочетаний
из трех элементов по пять, но с повторениями,
тогда такое возможно:
и имеем 11223. ■
Производящая функция для (п, r)-сочетаний с неограниченным числом повторений.
Найдем производящую функцию для (п, r)-сочетаний с условием, что хотя бы один элемент каждого вида появится в выборке. В этом случае будет иметь вид
=
=
=
=
=
.
(9)
Упростим полученную формулу
=
=
=
=
=
=
=
=
=
.
Здесь
.
Таким образом, число искомых r-сочетаний
равно нулю при
и
при
.Подобным
образом в производящей функции можно
учесть и другие требования, налагаемые
на (п,
r)-выборки.
Последовательность
называется возвратной,
если для некоторого k
и всех п
выполняется соотношение
,
(10)
где постоянные
коэффициенты
,
не зависят от п.
Многочлен
(11)
называется характеристическим многочленом для возвратной последовательности .
Перепишем (10) в виде
(12)
Если известны
начальные значения
то
по формуле (12) можно определить все
другие члены последовательности.
Соотношение (12) называют однородным рекуррентным соотношением.
Найдем формулу
общего члена
из (12). Для этого достаточно найти
производящую функцию последовательности
,
т.е. надо найти
=
.
Введем вспомогательный
многочлен
и найдем произведение
·
·
=
=
+
+…+
.
Степень многочлена
не превышает k
– 1, т.к. коэффициенты при
,
k
= 0,1,… Будут
равны нулю в силу уравнения (12).
Пусть характеристическое уравнение (11) имеет простые (может быть кратные) корни, т.е. его можно разложить
,
.
Тогда
=
=
=
.
Отсюда
=
,
и производящая функция может принять вид
=
.
Так как
,
то
и тогда
=
.
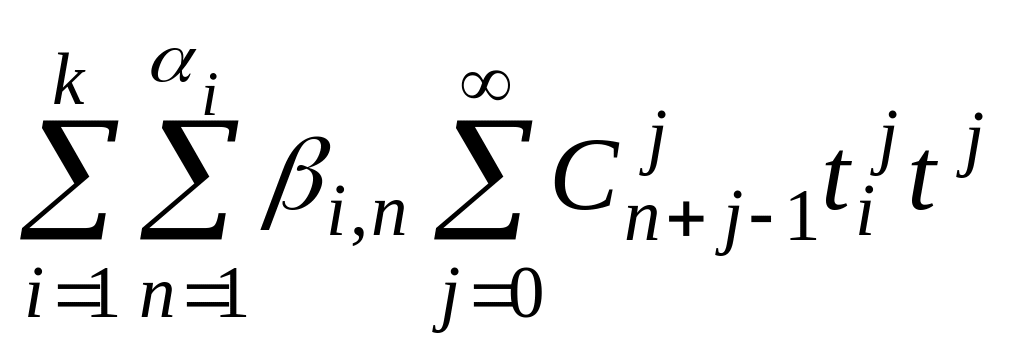(13)
Формула (13) дает
разложение производящей функции
последовательности
.
Для нахождения формулы общего члена
необходимо найти коэффициент при
в разложении (13).
Пример. Найти общий член последовательности , удовлетворяющей рекуррентному соотношению
,
если
,
.
□ Запишем данное рекуррентное соотношение в виде (12)
,
п =
0,1,…
Многочлен
=
.
Найдем
:
+
=
=
,
т.к.
,
.
Тогда
=
.
Методом неопределенных коэффициентов находим А и В:
,
,
.
Тогда
=
=
=
.
Следовательно, общий член последовательности имеет вид
=2,5
− 0,5·
.
Рассмотренный пример можно решить другим способом. Умножим заданное рекуррентное соотношение и просуммируем полученное выражение от нуля до бесконечности. В результате получим
или
,
или
.
Так как
=
, то
,
.
Тогда
)
)
+
,
− 2 – t – 4t + 8t +3t2 = 0.
Отсюда
=
И далее
=2,5 − 0,5· . ■
Рассмотрим несколько положений, позволяющих находить общее решение рекуррентных соотношений:
1. Возвратная последовательность (10) полностью определяется заданием ее первых k членов.
Действительно,
если
известны, то
.
2. Если t
является корнем характеристического
многочлена (11), то последовательность
удовлетворяет соотношению (10), т.е.
.
3. Пусть
− простые (некратные) корни
характеристического многочлена (11).
Тогда общее решение рекуррентного
соотношения (10) имеет вид
,
(14)
где
−
подходящие постоянные.
Действительно, то
что (14) удовлетворяет (10), следует из
того, что
является корнем характеристического
многочлена и, следовательно, удовлетворяет
(10), и из того, что если последовательности
и
удовлетворяют (10), то и последовательность
ему удовлетворяет при любых
и
.
Отметим, что если для любых существует единственный набор чисел таких , что
(15)
то может быть представлена в виде (14).
Определитель системы (15)
=
является определителем
Вандермонда. Он не равен нулю, если
при
,
что в нашем случае выполняется.
Следовательно, система линейных уравнений
(15) имеет единственное решение
относительно
.
4. Можно показать,
что если
есть корень характеристического
многочлена (11) кратности
,
то общее решение рекуррентного соотношения
(10) имеет вид
=
,
(16)
где
,
− произвольные постоянные, r
– количество кратных корней.
Пример. Решить неоднородное рекуррентное соотношение
.
□ Умножим заданное
рекуррентное соотношение
и просуммируем полученное выражение
от нуля до бесконечности. В результате
получим
или
,
или
.
Так как = , то
, .
Тогда
)
)
+
,
−
1 – 2t
– 3t(
−
1) +2t2
=
.
Отсюда
=
=
+
,
+
+
,
Тогда
=
=
=
=
=
.
Отсюда
=
.
■
Для упорядоченных (п,r)-выборок ((п,r)-перестановок) используются экспоненциальные производящие функции. Из определения упорядоченных и неупорядоченных (п, r)-выборок видно, что первых в r! раз больше, чем вторых. Поэтому в этом случае производящая функция имеет вид
,
(16)
где Р(п,
k)
– число (п,
k)-перестановок
из п
элементов по k,
т.е. размещения Р(п,
k)
=
.
Если на повторные
появления элементов никакие ограничения
не наложены, то в левой части формулы
(16) следует биномы
заменить на соответствующие многочлены
вида
.
Если же соответствующий
элемент допускает
повторений в выборках, то в левой части
формулы (16) следует биномы
заменить на соответствующие многочлены
вида
=
.
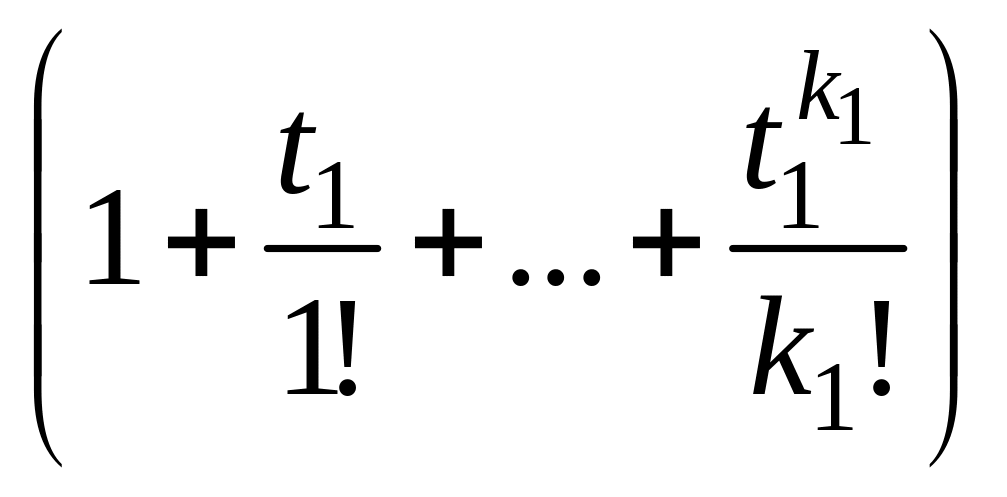
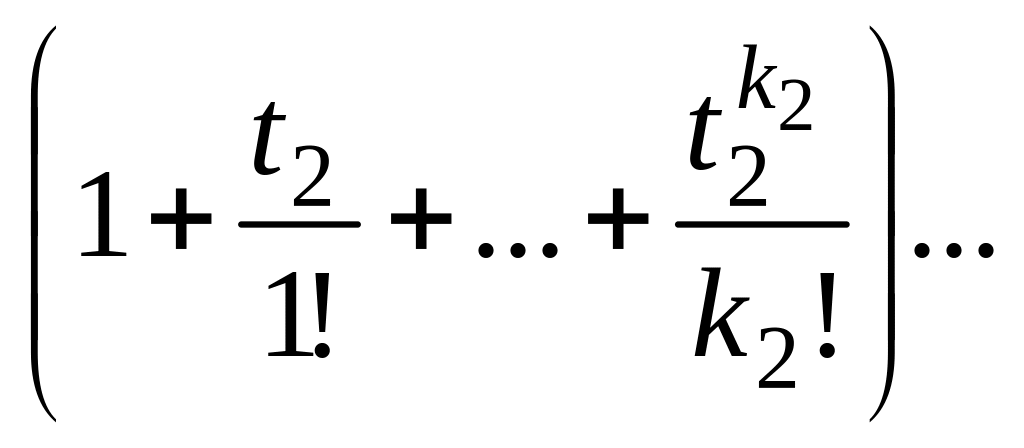
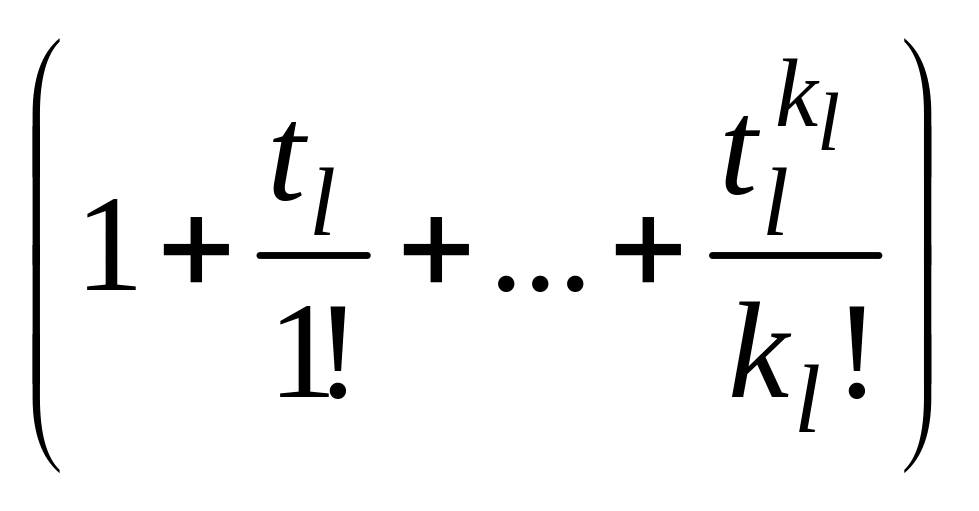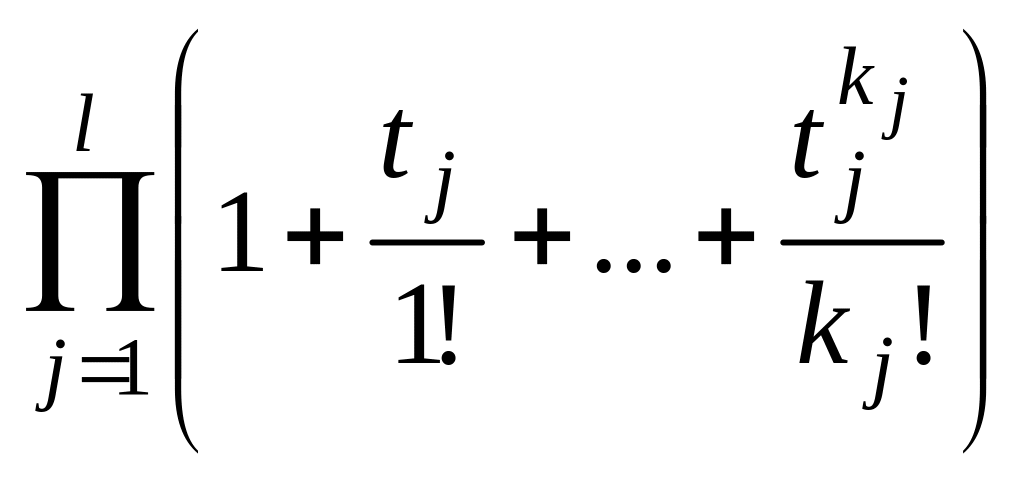Представление
этого произведения в виде ряда по
степеням t
дает в качестве коэффициентов при
числа k-перестановок,
допускающих указанные выше повторения.
Производящую функцию называют экспоненциальной в силу того, что эта функция для k-перестановок с неограниченным числом повторений из п элементов имеет вид
=
.
Так как производящая функция (и простая, и экспоненциальная) является степенным рядом, то в области его сходимости этот ряд можно почленно дифференцировать и интегрировать и, следовательно, получать новые степенные ряды и новые производящие функции. Например, возьмем
=
Почленное
интегрирование этого ряда в области
дает выражение для производящей функции
,
т.е.
.
Пример. Найти
экспоненциальную производящую функцию
последовательности
,
выраженную через производящую функцию
последовательности
,
если
=
,
п
= 0, 1, 2,… .
□ Используя понятие экспоненциальной производящей функции и проведя несложные преобразования, получим
=
=
=
=
=
=
=
=
.
■