Диаграмма Эйлера-Венна

Построение диаграммы Эйлера-Венна начинается с разбиения пространства U на областей с помощью п фигур (кругов Эйлера), где п – число различных множеств, входящих в пространство U . При этом каждая последующая фигура должна иметь одну и только одну общую область с каждой из ранее построенных областей. Такое разбиение называют символом Венна.

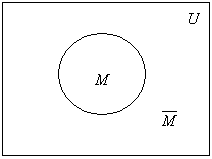
Пусть п = 1, т.е. U = {M}. Пространство разобьется на = = 2 области. При этом общей областью пространства U и множества М является само множество М:

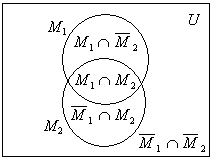
Пусть п = 2, т.е. U ={M₁, M₂}. Пространство разобьется на = = 4 области. При этом множество M₂ должно быть так построено, чтобы оно имело одну общую область с ранее построенным множеством M₁ и пространством U:

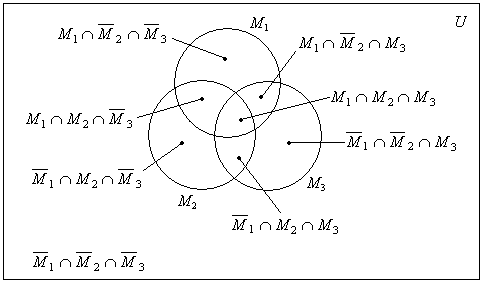
Пусть п = 3, т.е. U ={M₁, M₂, M₃}. Пространство разобьется на = = 8 областей. При этом множество M₃ должно быть так построено, чтобы оно имело одну общую область с каждой из ранее построенных областей: , , , :

Аналогично строятся символы Венна и для других значений п.

Каждой из областей соответствует пересечение множеств. Если теперь отметить некоторые области (согласно условию некоторой задачи), то получим диаграмму Эйлера-Венна. Объединение отмеченных областей определяет некоторое множество. Например, диаграмма Эйлера-Венна

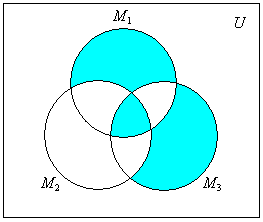
соответствует множеству

М(M₁, M₂, M₃) = .

§ 4. Бинарные отношения

Фундаментальным понятием дискретной математики является понятие отношения, которое используют для обозначения связи между объектами или понятиями. Наиболее часто встречающимися и хорошо изученными являются бинарные (или двухместные) отношения.

Бинарным отношением R в множестве М называется подмножество его квадрата : , где .

Два элемента находятся в отношении R , если , - двухэлементный кортеж.

Способы задания бинарных отношений

1. Матрица смежности

Матрица смежности – это матрица , каждой строке (столбцу) которой взаимно однозначно сопоставляют элемент множества М, тогда элемент c_ij , стоящий на пересечении i – ой строки и j – ого столбца, определяется следующим образом:

Пример. Задана блок-схема ЭВМ, предложенная фон Нейманом, которая состоит из множества устройств М={a,b,c,d,e}, где a – устройство ввода, b – процессор (арифметическое устройство), c – устройство управления, d – запоминающее устройство, e – устройство вывода. Если из устройства m_i поступает информация в устройство т_j ,то эти устройства находятся в отношении R , под которым понимается ин –

формационный обмен между этими устройствами. Задать отношение R в виде матрицы смежности.

□ Матрица смежности имеет вид

a b c d e

Построение искомой матрицы осуществлялось следующим образом: элемент множества М (устройство ЭВМ ), сопоставленный какой – либо строке матрицы, рассматривался на вопрос выполнения отношения R с каждым из элементов множества М (устройств ЭВМ ), сопоставленных столбцам матрицы. Если отношение R выполнялось, то на пересечении ставилась единица, в противном случае – нуль. Например, из устройства b (вторая строка) информация не поступает в устройство a (первый столбец) , значит, на пересечении ставился нуль; аналогично для пары устройств (b,b); из устройства b в устройство c (третий столбец) информация может поступать, значит, на пересечении ставилась единица; аналогично для пар устройств (b,d ) и

(b,e ). Тем самым была построена вторая строка матрицы и получены кортежи (b,c), (b,d ), (b,e). По этому правилу строились остальные строки матрицы смежности.

Множество полученных кортежей определяет отношение

R = {(a,b),(a,c),(a,d ),(b,c),(b,d ),(b,e),(c,a),(c,b),(c,d ),(c,e),(d,b),(d,c),(d,e),

(e,c)}.

Отношение R является подмножеством квадрата множества М , т.е. (что согласуется с определением бинарного отношения), где

М ² = = = {(a,a),(a,b),(a,c),(a,d),(a,e),(b,a),

(b,b),(b,c),(b,d),(b,e),(c,a),(c,b),(c,c),(c,d),(c,e),(d,a),(d,b),(d,c),

(d,d),(d,e),(e,a),(e,b),(e,c),(e,d),(e,e)}. ■

2. Граф

Совокупность множества М с заданным в нем бинарным отношением называется графом :

G = < M , R > ,

где М – носитель графа (множество вершин); R – сигнатура графа (множество дуг).

Пример. Построить граф G = < M , R > , задающий отношение R из предыдущего примера.

□ Искомый граф показан на рис. 1.9 :

G

Рис. 1.9

Здесь вершинами графа (кружки или точки) являются элементы множества М = {a,b,c,d,e} , т.е. устройства ЭВМ. Дуги (стрелки) указывают направление потока информации. При этом, если , то вершина - начало дуги, а вершина - конец дуги. ■

3. Фактор – множество

Окрестностью единичного радиуса элемента называется множество элементов таких, что

Множество окрестностей единичного радиуса , взятых для всех элементов множества М при задании в нем отношения

называется фактор – множеством множества М по отношению R.

Фактор – множество полностью определяет отношение R .

Пример. Задать бинарное отношение из рассмотренного примера в виде фактор – множества.

□ Фактор – множество строится в виде двух строк , в первой строке помещены элементы множества М , во второй под каждым элементом записывается окрестность единичного радиуса этого элемента .Тогда вторая строка задает фактор – множество М по R :

a b c d e

{b,c,d}{c,d,e}{a,b,d,e} {b,c,e}{c}. ■

4. Перечисление дуг графа ( множество упорядоченных пар )

Граф G = < M, R > , а значит , и бинарное отношение можно задать перечислением дуг графа (множеством упорядоченных пар).

Пример. □ Для рассмотренного примера будем иметь :

М = {a,b,c,d,e}, R = {(a,b),

}.

■