§ 6. Построение оптимального дерева бинарного поиска. Алгоритм гильберта – мура

Упорядоченным деревом называется ориентированное дерево, для которого определен порядок узла любой его вершины.

Пусть множество элементов, упорядоченных следующим образом: .

Бинарным деревом поиска для множества А является упорядоченное бинарное дерево, в котором каждая вершина v так помечена элементом множества А , что

1. для любой вершины и в любом поддереве вершины v имеет место упорядочение: ;

2. для любой вершины и в правом поддереве вершины v : ;

3. для любого элемента х из множества А существует единственная вершина v , помеченная меткой .

Пусть имеется некоторое подмножество универсума:

и - такое множество, что

1. представляет множество всех элементов , для которых ;

2. представляет собой множество всех элементов , для которых х < a₁ ;

3. b_n представляет собой множество всех элементов , для которых .

Другими словами, элемент b_i можно определить как

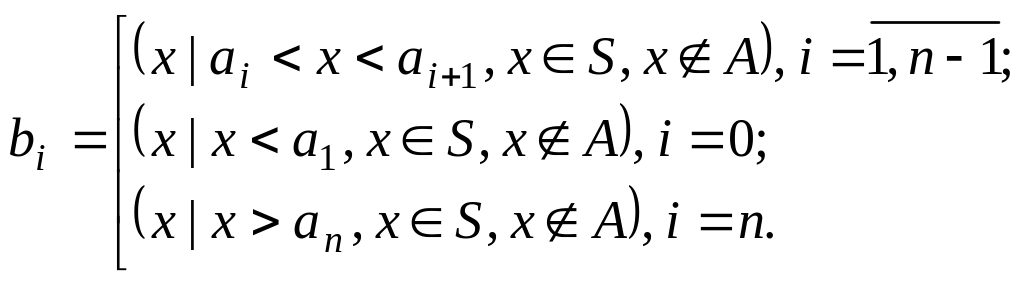
Расширенным деревом бинарного поиска для А называется дерево с п + 1 листьями (висячими вершинами), представляющими элементы множества В .

Пример. □ Деревья бинарного поиска для множества , где листья появляются слева направо, могут иметь вид:

■

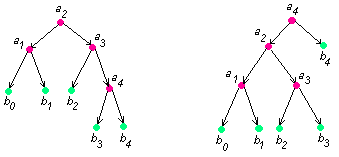
Пусть дано подмножество и дерево Т бинарного поиска для А. Множество S может быть множеством всех слов над английским алфавитом. Упорядочение может быть лексикографическим порядком. Необходимо определить, принадлежит ли элемент множеству А . Сравним х с элементом, который соответствует корню дерева Т . При этом могут возникнуть четыре случая, в соответствии с которыми продолжается поиск:

1. корень отсутствует (дерево Т бинарного поиска пусто). Значит, , поиск завершается безуспешно;

2. х равен элементу, соответствующему корню. Значит поиск завершается успешно;

3. х меньше элемента, соответствующего корню. Значит поиск продолжается ниже в левом поддереве корня;

4. х больше элемента, соответствующего корню. Значит поиск продолжается ниже в правом поддереве корня.

Успешный поиск завершается во внутренних вершинах, а безуспешный – в листьях дерева Т.

Глубина вершины v определяется как длина пути из корня до v.

Число сравнений, выполняемых до того, как завершается успешно во внутренней вершине v дерева Т, на единицу больше глубины вершины v. Если поиск завершается безуспешно в листе, то число выполненных сравнений равно глубине листа.

Пусть частоты обращения к элементам соответственно; частоты, с которыми поиск завершается в листьях . Тогда среднее время поиска в дереве Т ( по всем возможным ситуациям: успешным и безуспешным ) пропорционально стоимости дерева Т , определяемой как математическое ожидание количества сравнений поиска по данному бинарному дереву:

, ( 1 )

где глубина элемента а_i ; глубина элемента b_j .

Частоты p_i и могут быть интерпретированы как вероятности, тогда они должны быть неотрицательными и нормированными так, чтобы их сумма была равна 1:

.

Нормированные величины p_i и называются весами узлов и листьев соответственно.

Пример. Для деревьев из предыдущего примера заданы веса узлов и листьев:

.

Определить стоимости деревьев.

□ Проверим, являются ли заданные p и q вероятностями:

.

Определим стоимость первого дерева. Согласно формуле (1) стоимость дерева составит:

.

Аналогично можно определить стоимость для второго дерева. ■

Пусть даны неотрицательные веса p_i и . Необходимо построить дерево бинарного поиска минимальной стоимости для множества , элементы которого упорядочены следующим образом: , т.е. оптимальное дерево бинарного поиска (ОДБП) для весов .