§ 3. Построение остова экстремального веса. Алгоритм краскала

Рассмотрим алгоритм Краскала построения остова наименьшей длины (веса):

1. Упорядочить ребра графа по неубыванию их весов (длин):

2. Начиная с первого ребра в этом списке, добавляют ребра в строящийся остов, соблюдая условие: такое добавление не должно приводить к появлению цикла.

3. Повторять шаг 2 до тех пор, пока число ребер в строящемся остове не стане равным п – 1, где п – количество вершин в исходном графе.

Если упорядочить ребра по невозрастанию их весов (длин), то можно построить остов с наибольшим весом (длиной).

Пример. Построить остов с наименьшим весом для графа , заданного матрицей весов P

v₁ v₂ v₃ v₄ v₅ v₆

.

□ Так как матрица симметричная, то задан неориентированный граф. Исходный граф показан на рис. 6.2

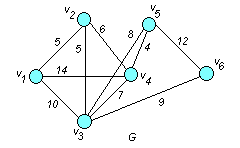
Рис. 6.2

1. Упорядочим ребра в порядке неубывания веса (длины):

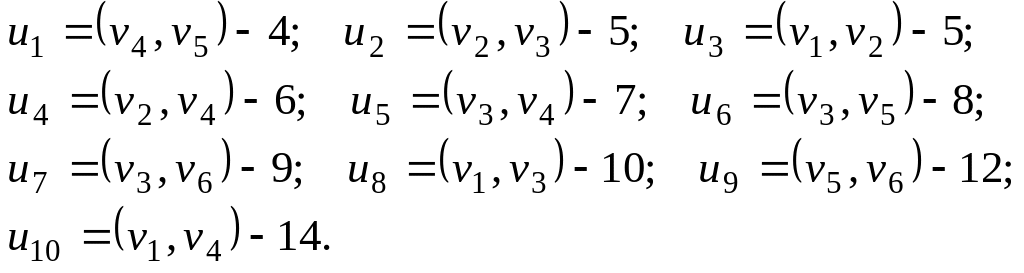
2. Возьмем ребро и₁ и поместим его в строящийся остов.

Возьмем ребро и₂ и поместим его в строящийся остов (т.к. оно не образует цикла с предыдущим ребром).

Возьмем ребро и₃ и поместим его в строящийся остов (т.к. оно не образует цикла с предыдущими ребрами).

Берем ребро и₄ и поместим его в строящийся остов.

Ребра и₅ и и₆ образуют с предыдущими ребрами циклы, поэтому их не используем в построении остова.

Берем ребро и₇ и поместим его в строящийся остов.

3. Проверим окончание алгоритма. Число входящих в остов ребер равно 5. Заданный граф имеет п = 6 вершин и п – 1 = 6 – 1 = 5. Таким образом, построенный остов содержит все вершины заданного графа. Вес (длина) построенного остова равна 4 + 5 + 5 + 6 + 9 = 29. Остов D наименьшего веса (длины) показан на рис. 6.3

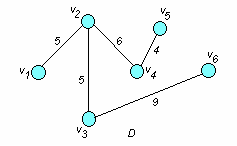
Рис. 6.3

■

§ 4. Метод ветвей и границ: задача коммивояжера. Общая модель задачи поиска

Задача коммивояжера относится к комбинаторным задачам на составление расписания. В свою очередь, к задаче коммивояжера сводятся многие другие задачи, связанные с объездом ряда пунктов и возвращением в исходный пункт: развозка почты, продуктов питания и т.д. Аналогичный характер носят задачи соединения отдельных пунктов линиями электроснабжения, водопровода, газоснабжения и т.п.

Постановка задачи коммивояжера: коммивояжер (агент, рекламирующий товар своей фирмы) должен посетить п городов ( в это число входит и город , из которого начинается поездка ) и вернутся в исходный пункт, побывав в каждом городе только один раз. Известны расстояния между городами (или стоимость проезда). Требуется установить, в каком порядке коммивояжер должен посещать города, чтобы общая длина маршрута (общая стоимость маршрута) была минимальной.

Если города принять за вершины графа, то задача коммивояжера сводится к определению кратчайшего гамильтонового контура.

Метод ветвей и границ является одним из вариантов поиска с возвращением (backtrak).

Рассмотрим общую модель задачи поиска.

Полагаем, что решение задачи состоит из вектора конечной, но не определенной длины, удовлетворяющего некоторым ограничениям и называемого частичным решением.

Каждое решение является элементом линейного упорядоченного множества Таким образом, при исчерпывающем поиске должны рассматриваться элементы множества в качестве возможных решений. В качестве исходного частичного решения выбирается пустой вектор и на основе имеющихся ограничений выясняется, какие элементы из являются кандидатами в . Обозначим это подмножество через В качестве а₁ выбираем наименьший элемент множества S₁. В результате имеем частичное решение

В общем случае различные ограничения, описывающие решения, говорят о том : из какого подмножества множества выбираются кандидаты для расширения частичного решения

от до .

Если частичное решение не представляет возможностей для выбора элемента a_k , то Ø . В этом случае следует вернуться и выбрать новый элемент . Если его выбрать нельзя, то возвращаемся еще дальше и выбираем новый элемент и т.д.

Этот процесс удобно описывать в терминах процедуры прохождения дерева в глубину. Исследуемое подмножество множества для I = 0,1,2,… представляется как дерево поиска следующим образом. Корень дерева (нулевой уровень) есть пустой вектор. Узлы первого уровня есть множество кандидатов для выбора а₁ . В общем случае узлы k-го уровня являются кандидатами на выбор a_k при условии, что а₁, а₂,…, выбраны.