§ 2. Максимальный поток через сеть. Алгоритм

ФОРДА – ФАЛКЕРСОНА

Функциональное назначение большинства физически реализованных сетей состоит в том, что они служат носителями систем потоков, т.е. систем, в которых некоторые объекты текут, движутся или транспортируются по системе каналов (дуг сети) с ограниченной пропускной способностью. Примерами могут служить потоки автомобильного транспорта по сети автодорог, грузов по участку железнодорожной сети, воды в городской сети водоснабжения, электрического тока в электросети, телефонных или телеграфных сообщений по каналам связи, программ в вычислительной сети. Ограниченная пропускная способность означает, что интенсивность перемещения соответствующих предметов по каналу ограничена сверху определенной величиной.

Наиболее часто в сети решается задача о максимальном потоке и минимальном разрезе.

Разрезом графа G называют некоторое множество дуг (ребер) этого графа, удаление которых делает этот граф несвязным.

Пусть задана сеть . Каждой дуге поставлено в соответствие неотрицательное число , называемое пропускной способностью дуги.

Пусть v – произвольная вершина сети. Обозначим через множество дуг, заходящих в v , а через множество дуг, выходящих из v.

Потоком сети называют функцию , удовлетворяющую условиям:

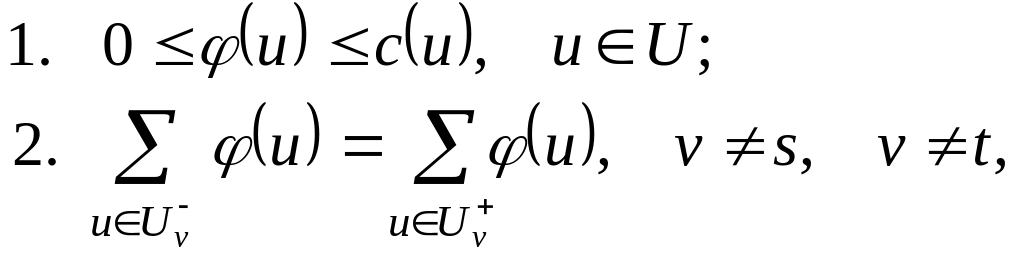
где вершина s – исток сети, а вершина t – сток сети.

Функцию можно рассматривать как количество вещества, протекающего (в единицу времени) по дуге от вершины v_i к вершине v_j .

Второе условие в определении потока называют условием сохранения потока: в промежуточных вершинах потоки не создаются и не исчезают. А это означает, что поток, выходящий из вершины истока s, в точности равен потоку, входящему в вершину стока t.

Величина называется остаточной пропускной способностью дуги .

Если , то дуга называется насыщенной.

Теорема. Максимальный поток через сеть G равен минимальной пропускной способности ее разреза.

Алгоритм Форда – Фалкерсона

Суть алгоритма: предположим, что в сети имеется некоторый поток и путь из s в t, состоящий из ненасыщенных дуг. Тогда очевидно, что поток в сети можно увеличить на величину , равную минимальной из остаточных пропускных способностей дуг, входящих в этот путь.

1. Перебираем все возможные “прямые” пути из s в t и проводим процедуру увеличения потока пока это возможно.

2. Не обращая внимания на ориентацию дуг, находим все возможные цепи, соединяющие вершины s и t. Возвращаясь к ориентации дуг, проводим процедуру увеличения потока, пока это возможно, для этих “ противоположных” путей.

3. В результате получим полный поток , т.е. поток, для которого каждый путь из s в t содержит по крайней мере одну насыщенную дугу.

4. Выбираем разрез сети, состоящий из насыщенных дуг, с минимальной пропускной способностью, значение которой равно значению максимального потока сети G .

Замечание. Для быстрого нахождения требуемого разреза рекомендуется изображать сеть с минимальным числом пересечений дуг.

Пример. Найти максимальный поток через сеть, заданную матрицей пропускных способностей дуг

v₁ v₂ v₃ v₄ v₅ v₆

□ Построим сеть G :

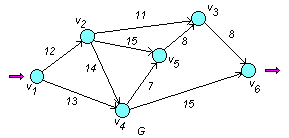
Исток (вершина входа сети) s = v₁ , сток (вершина выхода сети) t = v₆ .

1. Выбираем произвольно путь из вершины v₁ в вершину v₆ . Например, путь

.

Минимальную пропускную способность, равную 12, имеет дуга , т.е. . Увеличим по этому пути поток до 12 единиц. Дуга становится насыщенной. Дуги имеют на данный момент пропускную способность, равную 12.

Путь

, .

Здесь, согласно рассмотренному первому пути, пропускная способность дуги равна 12, но по условию ее пропускная способность равна 15. Значит, мы можем увеличить ее пропускную способность на 15 – 12 = =3 единицы. Следовательно, поток можно увеличить на 3 единицы. Дуга становится насыщенной. Дуга теперь имеет пропускную способность, равную 3.

Путь

. Поток можно увеличить на 7 единиц. Дуга становится насыщенной. Потоки на дугах примут вид:

, .

Больше “прямых “ путей нет, т.к. остальные пути проходят через насыщенные дуги.

2. Рассмотрим теперь “противоположные” пути. Отвлекаясь от ориентации дуг, выберем цепь, соединяющую вершины v₁ и v₆ без насыщенных дуг, например, цепь . Возвращаясь к ориентации дуг, получим “противоположный” путь:

,

. Следовательно, поток

можно увеличить на 1 единицу. Дуга становится насыщенной, .

Других маршрутов нет (другие маршруты проходят через насыщенные дуги).

3. Получен полный поток и он максимален.

4. Делаем разрез вокруг вершины v₆ по насыщенным дугам и получаем его величину единицы. Разрез и насыщенные дуги сети G показаны на рис. 6.1

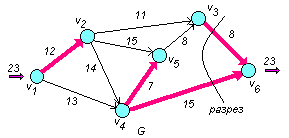
Рис. 6.1

■