Операции над множествами

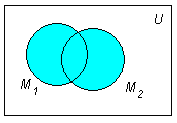
1. Объединением двух множеств М₁ и М₂ является множество М , состоящее из элементов, которые принадлежат хотя бы одному из множеств М₁, М₂ :

М =

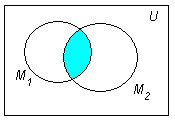
2. Пересечением двух множеств М₁ и М₂ является множество М , состоящее из элементов, которые принадлежат как множеству М₁ , так и множеству М₂ :

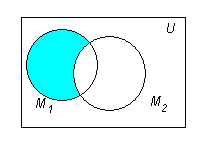
3. Разностью множеств М₁ и М₂ является множество М , состоящее из элементов, принадлежащих множеству М₁ и не принадлежащих множеству М₂ :

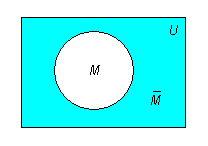
4. Дополнением множества М (до универсума U ) называют множество, определяемое из соотношения . Другими словами

Операции объединения и пересечения множеств можно обобщить на конечное и бесконечное число множеств. Используя указанные операции, можно выражать одни множества через другие, при этом сначала выполняется операция дополнения, затем пересечения и только потом операция объединения (разности). Для изменения этого порядка в выражении используют скобки. Например,

Для наглядности на рис. 1.2 изображены с помощью кругов Эйлера непересекающиеся множества и включение множества :

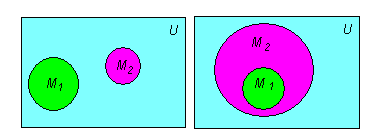
Ø

Рис. 1.2

Кортежем (упорядоченным множеством) называют совокупность элементов, в которой каждый элемент занимает определенное место.

Число элементов кортежа называют его длиной.

Например, является кортежем длины n с элемента-ми

Если элементы кортежа есть действительные числа, то такие кортежи называют векторами.

Например, кортеж можно рассматривать, как вектор в трехмерном пространстве. Тогда проекции вектора на оси координат определятся следующим образом:

i=1, 2, 3.

Можно определить проекции сразу на две оси, например, 1 и 2 :

Если кортеж имеет вид , то

и

- номера осей, причем

Прямым (декартовым) произведением множеств М₁ и М₂ называют множество М вида

,

где (m_i, m_j) – двухэлементные кортежи.

Отметим, что в общем случае

Операцию прямого произведения можно распространить на большее число множеств.

Пример. □ Пусть , . Тогда

■

Если некоторое множество М состоит из кортежей одинаковой длины, то проекцией этого множества на некоторую ось называют множество проекций кортежей из множества М на эту ось.

Пример. Определить проекции и , i=1, 2, 3 , если

М₁={(1,2,3,4,5),(2,1,3,5,5),(3,3,3,3,3),(3,2,3,4,3)},

M₂={(1,2,3,4),(2,1,3,5)},

M₃=

□ Сначала определим проекции множеств М₁ и М₂. Согласно определению проекции множества имеем:

, ,

,

Для определения и необходимо найти

:

Так как в множестве М₃ кортежи имеют разные длины, то проекций и не существует. ■

Легко проверить, что если , то

а если то