Глава V. Оптимизационные алгоритмы теории графов
Оптимизационные методы дискретной математики успешно применяются в многочисленных задачах управления производством, при проектировании физических систем с сосредоточенными параметрами (акустических, механических, электрических), при решении проблем генетики и проблем автоматизации проектирования и т.д. Если рассматривать область науки, связанную с ЭВМ, то такие дисциплины как теория цифровых автоматов, автоматизация проектирования, тестирование цифровых систем также широко используют оптимизационные методы дискретной математики. Знания, полученные в курсе дискретной математики, необходимы при разработке вычислительных устройств, систем и сетей, их аппаратного и программного обеспечения. Особое место занимают задачи, связанные с упорядочением и построением сложных цифровых систем путем рационального или оптимального соединения элементов, а также задачи, решение которых основано на построении отношений между раз-личными рода объектами.
Задачи такого рода, как правило, технологично ( удобно для человека ) формулируются и эффективно решаются с использованием графовой структуры, наглядно иллюстрирующей взаимосвязи между компонента-ми реальной системы.
§ 1. Определение кратчайших путей. Алгоритм дейкстры
Сетью называется ориентированный граф , в котором выделены две полюсные вершины , такие, что из одной вершины дуги только исходят (исток), а в другую вершину дуги только входят (сток).
В общем случае полюсных вершин может быть больше.
Пусть
- ориентированный граф (сеть) со взвешенными
дугами. Если две вершины не связаны
дугой, то вес полагается равным
бесконечности
.
Пусть некоторая вершина s - начало пути, а вершина t - конец пути.
Задача о
кратчайшем пути – частный случай
следующей задачи: найти в заданном графе
пути, соединяющие две заданные вершины
и доставляющие минимум или максимум
некоторой аддитивной функции, определенной
на путях. Чаще всего эта функция трактуется
как длина пути, и задача называется
задачей о кратчайших путях. Алгоритм
Дейкстры – одна из реализаций этой
задачи. Его часто называют алгоритмом
расстановки меток. В процессе работы
этого алгоритма узлам сети
приписываются числа (метки)
,
которые служат оценкой длины (веса)
кратчайшего пути от вершины s
к вершине vi
. Если вершина vi
получила на некотором шаге метку
,
то это означает, что в графе G
существует путь из s
в vi
, имеющий вес
.
Метки могут находиться в двух состояниях
– быть временными или постоянными.
Превращение метки в постоянную означает,
что кратчайшее расстояние от вершины
s
до соответствующей вершины vi
найдено.
Алгоритм Дейкстры имеет ограничение – веса дуг должны быть положительными. Сам алгоритм состоит из двух этапов. На первом этапе находится длина кратчайшего пути, на втором строится сам путь от вершины s к вершине t.
Этап 1. Нахождение длины кратчайшего пути.
Шаг 1. Присвоение вершинам начальных меток.
Полагаем
и считаем эту метку постоянной (постоянные
метки помечаются сверху звездочкой).
Для остальных вершин
полагаем
и считаем эти метки временными. Пусть
-
обозначение текущей вершины.
Шаг 2. Изменение меток.
Для каждой
вершины vi
c
временной меткой, непосредственно
следующей за вершиной
,
меняем ее метку в соответствии со
следующим правилом:
,
где
вес
дуги
.
Шаг 3. Превращение метки из временной в постоянную.
Из всех вершин
с временными метками выбираем вершину
с наименьшим значением метки:
Превращаем эту
метку в постоянную и полагаем
.
Шаг 4. Проверка на завершение первого этапа.
Если
,
то
длина кратчайшего пути от s
до t
. В противном случае происходит
возвращение ко второму шагу.
Этап 2. Построение кратчайшего пути.
Шаг 5. Последовательный поиск дуг кратчайшего пути.
Среди вершин, непосредственно предшествующих вершине с постоянными метками, находим вершину vi , удовлетворяющую соотношению
Включаем дугу
в искомый путь и полагаем
Шаг 6. Проверка на завершение второго этапа.
Если
то
кратчайший путь найден – его образует
последовательность дуг, полученных на
пятом шаге и выстроенных в обратном
порядке. В противном случае возвращаемся
к пятому шагу.
Пример. Задана весовая матрица Р сети G . Найти минимальный путь из вершины v1 в вершину v6 по алгоритму Дейкстры.
V1 v2 v3 v4 v5 v6
□ Построим граф (сеть) G :
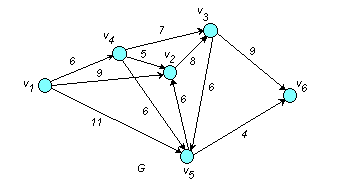
Этап 1. Нахождение длины кратчайшего пути.
Шаг 1. Присвоение вершинам начальных меток.
Полагаем
.
1-я итерация.
Шаг 2. Изменение меток.
Множество
вершин, непосредственно следующих за
с
временными
метками
.
Пересчитываем временные
метки этих вершин по формуле
;
Шаг 3. Превращение метки из временной в постоянную.
Одна из временных меток превращается в постоянную
=
Шаг 4. Проверка на завершение первого этапа.
,
происходит возвращение на второй шаг.
2-я итерация.
Шаг 2.
Шаг 3.
.
Шаг 4.
возвращаемся
на второй шаг.
3-я итерация.
Шаг 2.
Шаг 3.
Шаг 4.
возвращаемся на второй шаг.
4-я итерация.
Шаг 2.
Шаг 3.
Шаг 4.
возвращаемся на второй шаг.
5-я итерация.
Шаг 2.
Шаг 3.
Шаг 4.
конец первого этапа.
Длина кратчайшего
пути
.
Этап 2. Построение кратчайшего пути.
1-я итерация.
Шаг 5. Последовательный поиск дуг кратчайшего пути.
Составим множество
вершин, непосредственно предшествующих
с постоянными метками :
Проверим для этих двух вершин выполнение
равенства
Включаем дугу
в кратчайший путь.
Шаг 6. Проверка на завершение второго этапа.
возвращаемся
на пятый шаг.
2-я итерация.
Шаг 5.
.
Включаем дугу
в кратчайший путь.
Шаг 6.
завершение
второго этапа.
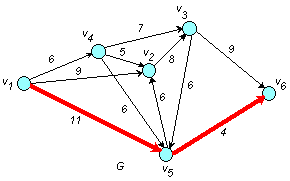
Кратчайший путь: (v1, v5), (v5, v6) .
Итак, кратчайший
путь от вершины v1
до вершины v6
построен. Его длина (вес) равна
15,
сам путь образует последовательность
дуг : (v1,
v5),
(v5,
v6)
:
■