§ 2. Операции над графами. Способы задания графов Операции над графами

Объединением графов и

называется граф , у которого и .

Пример. Заданы граф , у которого , и граф , у которого , Найти объединение этих графов.

□ По определению

, где и , следовательно,

Зная V и U, всегда можно построить граф G (рис. 4.5) :

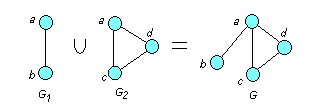
Рис. 4.5 ■

Суммой (соединением) графов и называется граф , представляющий собой объединение графов G₁ , G₂ и полного двудольного графа К_т,п , построенного на носителях и .

Другими словами, при построении суммы графов G₁ и G₂ определяется их объединение и каждая вершина , не вошедшая в пересечение , соединяется со всеми вершинами , не вошедшими в пересечение , и наоборот.

Пример. Найти сумму G₁ + G₂ графов G₁ и G₂ , рассмотренных в предыдущем примере.

□ По определению , где . Тогда , где V_k и U_k – множество вершин и множество ребер полного двудольного графа К_т,п соответственно. В двудольном графе множество вершин разбито на два непересекающихся подмножества и , т.е. , причем и . Определяем :

.

Тогда , . Полный двудольный граф имеет вид

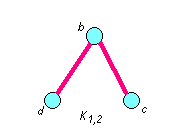
Объединяя три графа , получим искомый граф G (рис. 4.6):

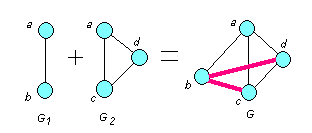
Рис. 4.6

В графе G тонкими линиями выделены ребра графа, который является объединением графов G₁ и G₂ (ср. с рис. 4.5 ), толстыми линиями – ребра полного двудольного графа К_1,2 . ■

Произведением графов G₁ = < V₁, U₁ > и G₂ = < V₂, U₂ > называется граф G=<V,U>, у которого , а множество ребер U получается следующим образом : вершины и смежны в графе G тогда и только тогда, когда или v_1m= v_1p, а v_2n и v_2k смежны в G₂ , или v_1m и v_1p смежны в G₁, а v_2n = v_2k .

Пример. Найти произведение графов G₁ и G₂ , у которых

, , , .

□ Согласно определению произведения графов :

.

Учитывая правило построения множества ребер U графа G , получим :

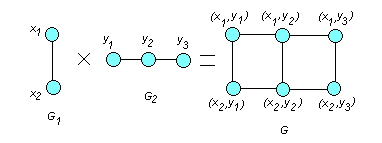
Рис. 4.7 ■

С помощью операции произведения можно ввести единичные п – мерные кубы – один из классов графов. Указанный п – мерный куб Н_п вводится рекуррентно:

,

где К₂ – полный граф с числом вершин, равным двум.

Таким образом, Н_n – граф порядка 2^п, вершины которого можно представить векторами длины п , причем такими, что векторы , соответствующие двум смежным вершинам, будут различаться ровно в одной координате. На рис. 4.8 представлены кубы Н₂ и Н₃ :

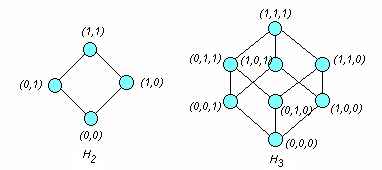
Рис. 4.8

Из рисунка видно, что каждая вершина п – мерного куба инцидентна п ребрам . Следовательно, число ребер п – мерного куба равно п·2^п-1 .