§ 5. Метод включений и исключений

Подсчет числа решений соответствующих задач не является единственным содержанием комбинаторного анализа. Метод включений и исключений позволяет решить важную задачу разделения множеств на подмножества в зависимости от того, обладают ли их элементы определенной совокупностью свойств или нет.

Рассмотрим сначала простую задачу о нахождении числа элементов объединения множеств. Пусть п(А) – число элементов множества А. Основная формула для нахождения числа элементов объединения двух множеств:

. (1)

Эта формула очевидна из диаграммы Венна:

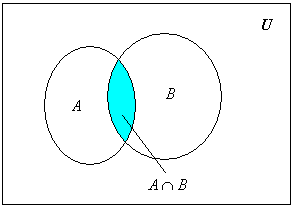
С помощью формулы (1) можно получить формулу для числа элементов объединения любого числа множеств. Например, для трех множеств:

= −

−

=

−

= .

Диаграмма Венна для этого случая:

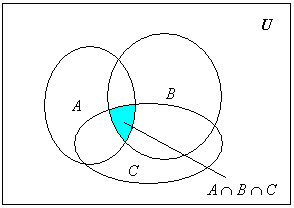
Для п множеств справедлива теорема.

Теорема 1. Если − некоторые множества и N(А₁) = | А₁|, N(А₂) = | А₂|, …, N(А_n) = | А_n|, то

−

+ …

. (2)

Обобщим формулу (2).

Пусть дано п-множество М некоторых элементов k-множество {р₁, р₂,…, р_k}, которыми элементы множества М могут как обладать, так и не обладать. Выделим какую-либо r-выборку свойств .

Пусть п − число элементов , обладающих всеми r выбранными свойствами. Отсутствие у элемента какого-либо свойства р_i обозначим через . Тогда, например, запись п означает число элементов, обладающих свойствами р₁ и р₃ и не обладающих свойством р₂.

Найдем число элементов, не обладающих набором определенных свойств, начав с самых простых случаев.

1. Пусть имеется одно свойство р, тогда п .

2. Имеется конечное число свойств р₁, р₂,…, р_k, несовместимых друг с другом. Тогда опять п = .

3. Элементы обладают комбинациями различных свойств. Тогда справедлива теорема:

Теорема 2. Если даны п-множество элементов и k-множество свойств р_i, , совместимых между собой, то

п = + − … +

+ . (3)

Примечательно, что формулу (3) можно использовать и в том случае, когда в ее левой части стоит любая комбинация свойств, как выполняющихся, так и не выполняющихся. Например, для левой части п формула примет вид

п = п − п − п +

+ п . (4)

Пример. В комнате находится несколько человек, знающих хотя бы один из трех языков. Шестеро знают английский, шестеро – немецкий, семеро – французский. Четверо знают английский и немецкий, трое – немецкий и французский, двое – французский и английский. Один человек знает все три языка. Сколько человек в комнате? Сколько из них знают только английский язык?

□ Данную задачу можно решить традиционным способом “вычерпывания” множеств без применения метода включений и исключений. Составим таблицу:

А	Н	Ф	АН	НФ	ФА	АНФ
6	6	7	4	3	2	1

Пусть из комнаты ушел человек, знающий все три языка. Тогда получим:

А	Н	Ф	АН	НФ	ФА	АНФ
5	5	6	3	2	1	0

Пусть теперь ушли три человека (из оставшихся), знающие одновременно английский и немецкий языки; число людей, знающих другие языки не изменится:

А	Н	Ф	АН	НФ	ФА	АНФ
2	2	6	0	2	1	0

Теперь пусть уйдут двое, знающие немецкий и французский языки:

А	Н	Ф	АН	НФ	ФА	АНФ
2	0	4	0	0	1	0

Наконец, уходит человек, знающий французский и английский языки. Окончательно получим:

А	Н	Ф	АН	НФ	ФА	АНФ
1	0	3	0	0	0	0

Таким образом, в комнате остался один человек, знающий только английский язык, и трое, знающих только французский язык. Кроме того, вышло семь человек, значит, сначала в комнате находилось одиннадцать человек.

Используем теперь для решения задачи метод включений и исключений. Пусть свойство р_А – знать английский язык; р_Н – знать немецкий язык; р_Ф – знать французский язык. По условию задачи общее число людей составляют вае, знающие хотя бы один язык; не знающих хотя бы один язык в задаче нет. По формуле (2) имеем

п = п + п + п − п − п − п +

+ п = 6 + 6 + 7 − (4 + 3 + 2) + 1 = 11.

Число людей, знающих только английский язык (по формуле (4)):

п = п − п −п + п =

= 6 − 4 − 2 + 1 = 1.

Так же легко может быть найден ответ и на другие подобные вопросы. ■

Пусть теперь элементы множества имеют веса. Веса – это числовые характеристики элементов рассматриваемых множеств.

Пусть задано п-множество М и каждому элементу приписан вес из k-множества свойств р₁, р₂,…, р_k. Тогда

а − сумма весов со свойством р_j.

Произведем r-выборку свойств и обозначим сумму весов элементов, обладающих всеми r выбранными свойствами, через , т.е. − это сумма весов элементов множества М, которые обладают каждым из свойств р₁, р₂,…, р_k. Сумму, распространенную на все возможные r-выборки свойств, обозначим = . Здесь суммирование распространяется на все сочетания длины r из k свойств, количество сочетаний равно . Таким образом, в суммируются веса только тех элементов, которые имеют как минимум r свойств. Пусть элемент обладает t свойствами и , тогда его вес в войдет раз. Например, = = содержит = k членов, а = = содержит членов и т.д. Через обозначим сумму весов всех элементов множества М, т.к. должна включать элементы, обладающие нуль свойствами и более. Положим − сумма весов элементов, обладающих ровно r свойствами из k имеющихся, тогда − сумма весов элементов, которые не имеют ни одного из указанных свойств. При таких обозначениях теорема включений и исключений с учетом весов формулируется следующим образом.

Теорема 3. Сумма весов элементов, обладающих точно r свойствами из k свойств р₁, р₂,…, р_k, равна

= +

=

= . (5)

Если все элементы имеют единичный вес, т.е. = 1, то = , и сумма весов равна числу слагаемых в сумме . Тогда формула (5) примет вид:

= . (6)

Теорема 4. Если даны п-множество М, каждый элемент которого имеет вес, и k-множества свойств, то сумма весов элементов, не удовлетворяющих ни одному из заданных свойств, определяется по формуле

= − + +…+

+ . (7)

Если все элементы имеют единичный вес, то = , и сумма весов равна числу слагаемых в сумме. В этом случае , равно числу элементов множества М, не удовлетворяющих ни одному из указанных k свойств. Тогда формула (7) примет вид:

п = + − … +

+ = . (8)

Пример. Пусть имеется конечное упорядоченное множество чисел 1, 2, …, п. Для них могут быть образованы перестановки . Число всех перестановок, очевидно, п!. Среди этих перестановок имеются такие, где ни один из элементов не сохранил своего первоначального места: . Такие перестановки называют беспорядками. Найти число беспорядков.

□ Множество п элементов рассматривается по отношению к множеству свойств элементов оставаться на своих местах р_i : . Очевидно, что если k элементов закрепляются на своих местах, то число N(k) соответствующих перестановок равно (п − k)!. Число способов, которыми можно выбрать k закрепленных элементов из общего количества п элементов, равно . Тогда число беспорядков, где ни один элемент не сохранил своего первоначального места, находится по формуле, аналогичной формуле (7):

N(0) = п! − + +…+ +…+

+ = п! − + +…+

+ +…=

= п! = .

Здесь выражение обозначает целую часть заданного числа, а е − основание натурального логарифма. ■

Пример. При опросе сотрудников некоторого учреждения оказалось, что 60% сотрудников знают английский язык, 50% − французский, 50% − немецкий, 30% − английский и французский, 20% − французский и немецкий, 40% − английский и немецкий, 10% − английский, французский и немецкий. Сколько процентов сотрудников:

а) не знают ни одного языка;

б) знают ровно два языка.

□ а) Можно воспользоваться формулой

= .

В нашем случае ее можно записать в виде

= ,

где свойство р_i, − это свойство знать i-й язык.

Тогда

= = − + − ,

где − общее число сотрудников, равное 1 или 100%; − число сотрудников, владеющих хотя бы одним языком; − число сотрудников, владеющих хотя бы двумя языками; − число сотрудников, владеющих тремя языками. Тогда

= 0,6 + 0,5 + 0,5 = 1,6; = 0,3 + 0,2 + 0,4 = 0,9; = 0,1.

Отсюда

= 1 − 1,6 + 0,9 − 0,1 = 0,2 ,

т.е. 20% сотрудников не владеют указанными языками.

б) Здесь можно использовать формулу

= .

Тогда, количество сотрудников, знающих ровно два языка:

= = − = 1· 0,9 − 3· 0,1 = 0,6 ,

т.е. 60% сотрудников владеют двумя языками. ■

В случае, когда свойств немного, для решения задач подобного типа удобно использовать круги Эйлера.

Пример. В группе студентов 25 человек. Среди них 20 сдали сессию успешно, 12 занимаются в спортивных секциях, причем 10 из них сдали сессию успешно. Сколько неуспевающих студентов не посещает спортивных секций?

□ Изобразим множество студентов, успешно сдавших сессию, кругом, помеченным буквой У, а множество тех, кто занимается в секциях, кругом, помеченным буквой С:

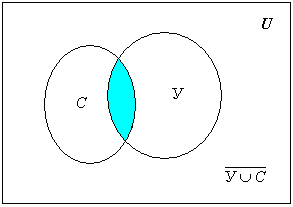
Пересечение кругов соответствует множеству успевающих студентов, занимающихся в секциях, а объединение – множеству студентов, которые учатся успешно или посещают секции. Число таких студентов равно

20 + 12 – 10 = 22.

Число тех неуспевающих студентов, которые не посещают секций, равно

25 – 22 = 3. ■

Пример. Найти число способов разложения п шаров по т ящикам так, чтобы r ( ) ящиков остались пустыми.

□ Очевидно, что порядок шаров важен, т.е. шары следует пронумеровать. Следовательно, будут иметь место п-перестановки. В данном опыте выбирается ящик. Это выборка с повторениями, т.к. ящики могут повторяться, например, первый шар положен в первый ящик, второй шар положен в первый ящик и т.д. Следовательно, речь идет о выборке т ящиков п раз ( п шаров) с повторениями. Таким образом, число способов, которыми можно разместить п шаров по т ящикам, равно т^п.

Пусть теперь p_i ( ) – свойство, состоящее в том, что при данной раскладке ящик с номером i остался пустым. Тогда количество раскладок, обладающих свойствами при одном способе выбора r пустых ящиков, равно = , а общее число раскладок, распространенное на все возможные способы выбора пустых ящиков, будет равно

= .

Используя формулу (6) в наших обозначениях, получим

= = .

Пусть т = 3, п = 5, r = 1. Тогда

= = 1·3·2⁵ −2·3·1⁵ + 3·1·0⁵ = 3·32 − 2·3 + 0 = 90.

Следовательно, существует 90 способов разложения пяти шаров по трем ящикам так, чтобы один ящик остался пустым. ■

Рассмотренная задача является одной из широкого круга задач на “распределение объектов любой природы по ячейкам”. Ход решения задачи показал, что необходимо тщательно анализировать “физический смысл задачи”, чтобы правильно решить вопрос о том, следует ли считать распределяемые объекты одинаковыми или различными, учитывать их порядок, или нет, считать ячейки одинаковыми или различными.

Постановка задачи

Предполагается, что даны n объектов и k ячеек (“ящиков”). Ставится вопрос о количестве способов, которыми можно распределить объекты по ячейкам. При этом в зависимости от условия задачи возможны следующие допущения:

1)объекты могут бытьодинаковыми или различными;       2) ячейки могут быть одинаковыми или различными (разные ячейки удобно различать по номерам);       3) ограничения на количество объектов в ячейках;       4) могут использоваться не все объекты и не все ячейки;       5) может учитываться порядок объектов в ячейках и порядок самих ячеек.

Одинаковые объекты

      1. Вместимость объектов не ограничена.

Расположив все объекты на прямой, получим (n − 1) интервалов между ними. Выберем (k − 1) интервалов и разместим в них “перегородки”, тем самым получим распределение объектов по непустым ячейкам:

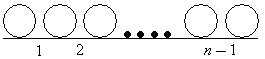
Всего существует способов такого размещения перегородок, следовательно, различных способов распределения n одинаковых объектов по k непустым ячейкам.

2. Добавим к имеющимся n объектам еще k таких же и распределим полученные (n + k) объектов по k ячейкам так, чтобы среди ячеек не было пустых. При этом n исходных объектов распределяется по ячейкам произвольным образом. Число способов такого распределения равно:

.

3. Ограничение на количество объектов в ячейке.

Пусть в каждой ячейке должно быть не менее m объектов. Тогда сначала кладем в каждую ячейку по m объектов, а затем рассматриваем всевозможные способы распределения оставшихся (n−km) объектов. Число способов распределения равно:

.

Различные объекты

1. Распределение различных объектов без учета порядка объектов в ячейках.

а) Вместимости ячеек не ограничены .

Первый объект можно поместить в любую из k ячеек; второй, независимо от первого, – также в любую из k ячеек и т.д. Тогда по правилу произведения объекты можно распределить по ячейкам различными способами (это есть число n-перестановок с неограниченными повторениями из k элементов).

б) Ячейки имеют заданные вместимости.

Пусть ячейки имеют заданные вместимости , причем:

.

Тогда объекты для первой ячейки можно выбрать способами, для второй – способами и т.д. По правилу произведения число способов заполнения всех ячеек равно

· ·…· = .

Это есть количество соответствующих n-перестановок.

в) Отсутствие пустых ячеек

Пусть каждая ячейка не пуста. На основании принципа включения и исключения получим, что число распределений n объектов по k ячейкам определяется как

.

2. Распределение различных объектов с учетом их порядка в ячейках

а) Без ограничений на число объектов в ячейках

Как было показано ранее, если объекты не различать между собой (объекты одинаковы), то число способов распределения равно . Каждому такому способу распределения одинаковых объектов по ячейкам соответствует n! способов распределения разных объектов с учетом их порядка, которые получаются за счет перестановок объектов между собой (не изменяющих числа объектов в ячейке), т.е. при учете порядка каждое такое распределение порождает n! распределений.

По правилу произведения получаем формулу для числа всех способов распределения:

· n! = .

б) Отсутствие пустых ячеек

Без учета порядка число распределений, как показано ранее, равно . При учете порядка каждое такое распределение порождает n! распределений. По правилу произведения общее число распределений равно

· n! = .

Метод включений и исключений может быть использован при решении некоторых задач теории чисел и ее приложений, где применяются специальные функции Эйлера и Мебиуса.

Функцией Эйлера называется функция , определенная на множестве N, значения которой равны числу k натуральных, может быть, и составных целых чисел, взаимно простых с п и 0 < k < n, (k, n) = 1. Для п = 1 полагают .

Запись (a, b) обозначает наибольший общий делитель натуральных чисел a и b. Взаимно простыми являются числа, наибольший общий делитель которых равен единице. Например, натуральные числа 5 и 7 взаимно простые, т.к. (5, 7) = 1. Таким образом, взаимно простые числа друг на друга нацело не делятся.

Функция Эйлера аналитически выражается следующим образом:

= п − + + …+ , (9)

где k − есть число простых делителей q_i числа п, .

Чаще функция Эйлера используется в другом виде:

= п = , (10)

где п = − разложение аргумента на простые сомножители.

Пример. Найти значения функции Эйлера для п = 1, 2,…, 10.

□ Разложим числа от 1 до 10 на простые делители:

1 = 1¹, 2 = 2¹, 3 = 3¹, 4 = 2², 5 = 5¹, 6 = , 7 = 7¹, 8 = 2³, 9 = 3², 10 = .

Найдем значения функции.

1. по определению;

2. = = 1, (1,2) = 1; это число 1;

3. = = 2, (1,3) = 1, (2,3) = 1; два числа не превосходят число 3 и взаимно просты с числом 3, эти числа 1 и 2;

4. = = 2, (1,4) = 1, (3,4) = 1; это числа 1 и 3;

5. = = 4, (1,5) = 1, (2,5) = 1, (3,5) = 1, (4,5) = 1; это числа 1, 2, 3, 4;

6. = = 2, (1,6) = 1, (5,6) = 1; это числа 1 и 5;

7. = = 6, (1,7) = 1, (2,7) = 1, (3,7) = 1, (4,7) = 1, (5,7) = 1, (6,7) = 1; это числа 1, 2, 3, 4, 5, 6;

8. = = 4, (1,8) = 1, (3,8) = 1, (5,8) = 1, (7,8) = 1; это числа 1, 3, 5, 7;

9. = = 6, (1,9) = 1, (2,9) = 1, (4,9) = 1, (5,9) = 1, (7,9) = 1, (8,9) = 1; это числа 1, 2, 4, 5, 7, 8;

10. = = 4, (1,10) = 1, (3,10) = 1, (7,10) = 1, (9,10) = 1; это числа 1, 3, 7, 9; ■

Свойства функции Эйлера:

1⁰. Если (a, b) = 1, то .

Действительно, пусть (3,7) = 1,

;

Ранее было показано, что = 2, = 6. Тогда · = 2·6 = 12, т.е. .

2⁰. .

Действительно, пусть п = 8 = 2³. Ранее было показано, что = 4. Теперь воспользуемся указанной формулой , т.е. равенство получено.

3⁰. = = п .

4⁰. ,

где d – различные делители числа п.

Например, если п = 10 = , то . Выражение означает, что суммирование ведется по всем делителям числа 10, т.е.

1 + 1 + 4 + 4 = 10.

5⁰. , где п > 0 и (х, п) = 1.

Например, х = 3, п = 7. Тогда 729 = 104·7 + 1 = или х = 3, п = 10. Тогда 81 = 8·10 + 1 = .

Функция Мебиуса определяется для всех и равна

где п = − разложение аргумента на простые сомножители.

Значения функции Мебиуса для первых десяти значений аргумента :

n	1	2	3	4	5	6	7	8	9	10
	1	−1	−1	0	−1	1	−1	0	0	1

Свойства функции Мебиуса:

1⁰.

причем суммирование идет по всем делителям d числа п. Так, если п = 1, то . Если же п = , то = (1 – 1)^k = 0, т.к. все делители d, для которых , имеют по определению вид , т.е . Количество таких делителей , выбираемых из , равно .

2⁰. Если , то , где и определены на множестве N. Указанная формула называется формулой обращения Мебиуса.

3⁰. .

Данная формула устанавливает связь между функциями Эйлера и Мебиуса. Если

п = , то = .