§ 3. Бином и полином

Запишем формулы бинома.

Для

(1)

Если заменить b на − b, то из формулы (1) следует:

, (2)

где коэффициенты называют биномиальными коэффициентами.

Для всех неотрицательных целых чисел п, k

(3)

Область определения биномиальных коэффициентов можно расширить:

для функция

(4)

является биномиальным коэффициентом.

Для целых оба определения для биномиальных коэффициентов совпадают.

Замечание: читается: С из п по k ; п над k .

Примеры.

□ 1)

2)

3)

4) . ■

Свойства биномиальных коэффициентов

Числа имеют ряд важных свойств:

1⁰ для целых справедливо свойство симметрии

2⁰ теоремы сложения:

из формулы бинома при а = 1, b = 1 следует:

,

это число равно числу всех возможных неупорядоченных подмножеств множества М, состоящего из п элементов (булеан),

при а = 1, b = −1 :

,

из этого равенства следует, что суммы биномиальных коэффициентов, стоящих на четных и нечетных местах, равны между собой и каждая равна ;

;

3⁰ для теоремы сложения имеют вид :

.

Формула полинома является обобщением формулы бинома, т.е.

для любых действительных чисел а₁, а₂, … , а_т не равных нулю и любого натурального числа п имеет место формула:

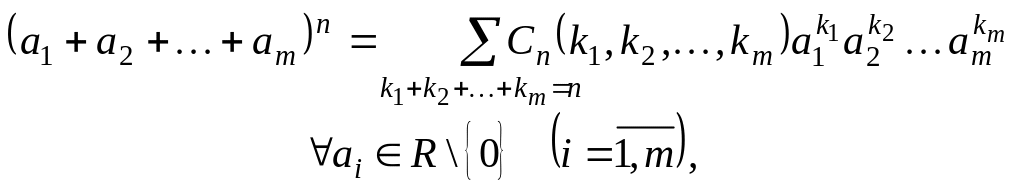(5)

при этом суммирование распространяется на все наборы натуральных чисел для которых .

Коэффициенты

,

определенные для всех натуральных п и всех наборов неотрицательных чисел , для которых , называют полиномиальными коэффициентами.

Полиномиальные коэффициенты часто записывают в виде .

При формула (5) принимает вид

(6)

Пример. □

■

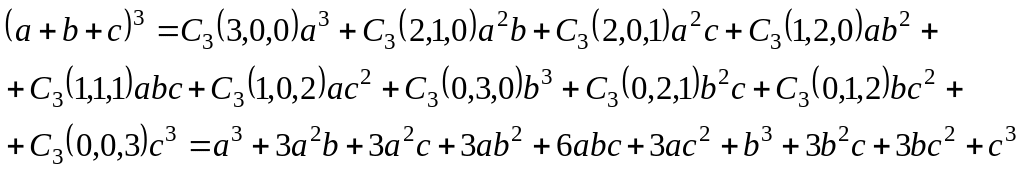
§ 4. Подстановки

Взаимно однозначное отображение конечного упорядоченного множества из n элементов на себя называется подстановкой n- й степени.

Пример.

□ Рассмотрим подстановку пятой степени

.

Здесь осуществляется отображение: число 1 первой строки переводится в число 3 второй строки; число 2 первой строки переводится в число 1 второй строки; число 3 – в 5; число 4 переводится в 4, как говорят, остается на месте; число 5 – в 2. ■

Часто подстановку задают только нижней строкой .

Подстановку, при которой на месте остаются все элементы, называют тождественной :

.

Подстановки можно перемножать. Операция произведения подстановок и состоит в последовательном их применении.

Пример. Найти произведение подстановок

□ Имеем

Здесь в первой подстановке 1 переходит в 2, а во второй подстановке 2 переходит в 1. Следовательно, в результирующей подстановке 1 будет переходить в 1. Аналогично поступают и с другими элементами. ■

Можно перемножать только подстановки одинаковой степени (совместимые ). Умножение подстановок n-й степени при некоммутативно.

Пример. Показать, что произведение подстановок из предыдущего примера некоммутативно.

□ Перемножим подстановки в обратном порядке :

Можно видеть, что результаты умножения не совпадают : . ■

Подстановки на множестве М = {1, 2, … ,n } образуют группу относительно операции произведения. Действительно, справедливы следующие утверждения:

1. Для любых двух подстановок элементов множества М = {1, 2, … ,n } произведение есть однозначно определенная подстановка;

2. Произведение подстановок ассоциативно, но не коммутативно:

;

3. Единичным элементом группы является тождественная подстановка :

;

4. Для любой подстановки существует обратная подстановка , т.е. если то существует обратная подстановка , при этом .

Группа подстановок на множестве М ={1,2,…, n} называется симметрической группой п-й степени и обозначается через S_n. Порядок симметрической группы п-й степени (число ее (группы) элементов) равен n!.

Пример.

□ Элементы симметрической группы S₃ :

Порядок группы S₃ равен 3! = 6. ■

Если в матрице подстановки элементов множества М={1,2, … ,n}

встречаются два столбца, для которых s_i < s_j , t_i > t_j ( или s_i > s_j , t_i < t_j ), то такая пара столбцов называется инверсией подстановки .

Подстановка называется четной или нечетной в зависимости от того, четно или нечетно число встречающихся в ней инверсий.

Пример. □ Пусть − число инверсий подстановки , то для подстановки из предыдущего примера будем иметь:

Подстановки − нечетные, − четные, тождественная подстановка не является четной или нечетной. ■

Неподвижной точкой подстановки называется элемент , для которого .

Например, в подстановках группы S₃ ( см. выше ) имеет три неподвижные точки; − одну неподвижную точку 3; точку 2; и − не имеют неподвижных точек; − одну, равную 1.

Если матрицу подстановки перестановкой столбцов можно привести к виду

то задает взаимно однозначное отображение

множества на себя, которое называется циклом длины r и обозначается

Каждой неподвижной точке соответствует цикл длины 1. Каждую подстановку можно однозначно представить в виде произведения циклов, не имеющих общих элементов.

Пример. □ Данные подстановки можно записать в виде произведения следующих циклов:

■