Правила суммы и произведения

Основной комбинаторной задачей является подсчет числа (п, r)-выборок при различных условиях. Практический опыт таких подсчетов привел к двум логическим правилам.

Правило суммы

Теоретико-множественная формулировка.

Если даны п-множество М₁ (т.е. |М₁| = n) и т-множество М₂, то при Ø объединение будет (п + т)-множеством.

В более общем случае. Если

Ø , ,

и если М_i есть п_i-множество, то множество М есть -множество.

Комбинаторная формулировка.

Пусть

объект a₁ может быть выбран т₁ способами ;

объект а₂ может быть выбран т₂ способами ;

………………………………………………………..

объект а _k может быть выбран т _k способами .

Тогда выбор объекта а₁ , либо объекта а₂ , … , либо объекта а _k может быть осуществлен т₁ + т₂ + … + т _k способами.

Пример. Фирма направляет специалиста в командировку в другой город, в который в течение суток отправляются 6 поездов, 4 автобуса и 1 самолет. Сколько существует способов добраться до этого города ?

□ По правилу суммы всего существует 6+4+1=11 способов выехать в назначенный город. ■

Правило произведения

Теоретико-множественная формулировка.

Пусть М₁, М₂, … , М _k - конечные множества , М = - их декартово произведение, тогда =

Комбинаторная формулировка.

Пусть

объект а₁ выбирается т₁ способами ;

и после такого выбора

объект а₂ выбирается т₂ способами ;

………………………………………………

и после таких выборов

объект а _k выбирается т _k способами .

Тогда выбор упорядоченного множества объектов может быть осуществлен способами.

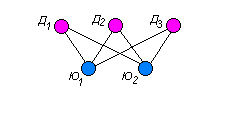
Пример. На дискотеку пришли 3 девушки и 2 юноши. Сколько танцующих пар они могут составить ( не одновременно ) ?

□ По правилу произведения можно составить 2 пар. Решение можно представить в виде диаграммы (графа), иллюстрирующего декартово произведение множеств :

■

§ 2. Формулы расчета перестановок и сочетаний

Найдем число всех возможных (п, r)-перестановок без повторений (т.е. размещений). Задача решается с помощью последовательного применения правила произведения. Действительно, в п-множестве М имеется п возможностей для выбора первого элемента (п, r)-перестановки; для выбора второго элемента останется п – 1 возможностей. Аналогично рассуждая, получаем, что для выбора r-го элемента останется п – r + 1 возможностей. Тогда

. (1)

Действительно,

.

Здесь принято 0! = 1! = 1.

Таким образом, число упорядоченных r-элементных подмножеств множества М, состоящего из п элементов, равно

.

В частности, если п = r, то получаем перестановки и = Р(п, п) = = п!. Это число способов упорядочения п-элементного подмножества.

Пример. В турнире участвуют 8 команд. Сколько различных прогнозов относительно трех первых мест по результатам соревнований можно сделать?

□ Требуется определить число различных способов распределения трех первых мест при восьми командах, т.е. найти число различных размещений (т.к. каждая команда может занять либо первое, либо второе, либо третье место) из 8 команд по 3 команды:

= . ■

Подсчитаем число всех возможных (п, r)-перестановок с повторениями (т.е. размещений с повторениями). В этом случае после выбора любого элемента (п, r)-перестановки остаются все те же п возможностей для выбора следующего элемента. Следовательно, по правилу произведения число (п, r)-перестановок с повторениями (размещений с повторениями ) равно:

. (2)

Пример. Сколько различных трехбуквенных слов можно составить из 32 букв алфавита?

□ Так как в словах могут быть одинаковые буквы, то имеют место размещения с повторениями. Так как п = 32, r = 3, то

. ■

Определим число (п, r)-сочетаний. Пусть имеется ряд неупорядоченных (п, r)-выборок без повторения элементов. Сравним числа и . Здесь − число упорядоченных выборок из п элементов по r; − число неупорядоченных выборок из п элементов по r. Каждую неупорядоченную выборку объема r можно упорядочить r! Различными способами, т.е. r! = . Отсюда

= .

Таким образом, число всех неупорядоченных r-элементных подмножеств множества М, состоящего из п элементов, равно

= . (3)

Пример. Сколькими способами можно выбрать 3 книги из 5?

□ Так как порядок книг в трехэлементном наборе безразличен, то имеют место сочетания. Имеем п = 5, r = 3, тогда

= = . ■

Рассмотрим более сложную задачу. Пусть

Ø , , причем М_i есть r_i-подмножество множества М . Очевидно, что . Рассуждаем аналогично тому, как это делалось при нахождении числа . Для выбора r₁-подмножества М₁ из М имеется возможностей; после этого r₂-подмножество М₂ можно выбрать только из оставшихся п − r₁, т.к. Ø. Этот выбор можно осуществить способами и т.д. Применяя правило произведения, получим число способов, которыми можно представить множество М из п элементов в виде сумме k неупорядоченных множеств М₁, М₂,…, М_k, число элементов которых составляет соответственно r₁, r₂,…, r_k, равно

.

Полученную формулу можно использовать при вычислении перестановок с повторениями, т.е.

. (4)

Пример. Сколько различных шестизначных чисел можно составить из цифр 1, 1, 1, 5, 5, 9 ?

□ Так как в изображении числа присутствую одинаковые числа: цифра 1 присутствует 3 раза, а цифра 5 – 2 раза, то имеют место перестановки с повторениями. Дано: п = 6, r₁ = 3, r₂ = 2, r₃ = 1. Тогда

. ■

Найдем число (п, r)-сочетаний с повторениями из множества М. Пронумеруем элементы множества М числами 1, 2,…, n. Тогда вместо (п, r)-сочетаний множества М можно рассматривать (п, r)-сочетания из эквивалентного ему множества в силу взаимно однозначного соответствия.

Всякая (п, r)-выборка из может быть записана в виде , где (равенство возможно, т.к. рассматриваются выборки с повторениями). Далее, r-выборке поставим в соответствие r-множество , в котором все элементы уже различны. Соответствие между и опять взаимно однозначное, причем r-множества являются r-сочетаниями без повторений из -множества . По формуле (3) число -сочетаний без повторений равно . Тогда

= = . (5)

Пример. Как велико число различных результатов бросаний двух не отличимых друг от друга кубиков ?

□ Так как предполагается, что в комбинациях a : b и b : а, где а и b − очки на кубиках, порядок безразличен ( например, 1:3 и 3:1 считаются одной комбинацией) и могут присутствовать комбинации a : а (например, 1:1 или 3:3), то имеют место сочетания с повторениями. Дано: п = 6, r = 2, тогда

= = . ■