
- •Глава I
- •§ 1. Определение графа
- •§ 2. Подграфы
- •§ 3. Операции над графами
- •§ 4. Цепи, циклы, компоненты
- •§ 5. Степени вершин графа
- •§ 6. Матрицы, ассоциированные с графом
- •§ 7. Регулярные графы
- •§ 8. Метрические характеристики графа
- •§ 9. Критерий двудольности графа
- •§10. Реберный граф
- •§ 11. Группа автоморфизмов графа
- •§ 12. «Почти все» графы
- •Упражнения
- •Глава II Деревья
- •§ 13. Определение дерева
- •§ 14. Матричная теорема Кирхгофа
- •§ 15. Остов минимального веса
- •Упражнения
- •Глава III
- •§ 16. Азбука теории матроидов
- •§ 17. Двойственный матроид
- •§ 18. Примеры матроидов
- •§ 19. Изоморфизм матроидов
- •§ 20. Представление матроида
- •§ 21. Бинарные матроиды
- •§ 22. Трансверсали
- •§ 23. Жадный алгоритм
- •§ 24. Объединение и пересечение матроидов
- •Глава IV Независимость и покрытия
- •§ 25. Независимые множества и покрытия
- •К. Шеннон ввел параметр
- •§ 26. Клика
- •§ 27. Проблемы клики, изоморфной вложимости и изоморфного подграфа
- •§ 28. Интерпретации независимых множеств
- •§ 29. Паросочетания
- •§ 30. Паросочетания в двудольном графе
- •§ 31. Двудольные графы и семейства подмножеств
- •§ 32. Паросочетания и покрытия
- •Упражнения
- •Глава V
- •§ 33. Вершинная связность и реберная связность
- •Чтобы учесть эту и подобные ей ситуации, естественно ввести следующее распределение: максимальный k-связный подграф графа называется его k-связной компонентой, или просто k-компонентой.
- •§ 34. Двусвязные графы
- •§ 35. Теорема Менгера
§ 7. Регулярные графы
Граф называется регулярным (или однородным), если степени всех его вершин равны; степенью регулярного графа называется степень его вершин. Степень регулярного графа G обозначается через deg G.
Все полные графы регулярны. Графы платоновых тел также регулярны. Регулярным графом степени n является n-мерный куб Qn.
Из леммы о рукопожатиях вытекает, что не существует регулярного графа, порядок и степень которого нечетны.
Утверждение 7.1. Пусть натуральные числа n и d, среди которых есть четное, удовлетворяют неравенствам 0<=d<=n-1. Тогда существует регулярный граф порядка n и степени d.
> Для d = 0 утверждение очевидно. Кроме того, если G — регулярный граф порядка n степени d, то дополнительный граф также регулярен и deg =n-1-d. Поэтому достаточно рассмотреть случай, когда 0 < d <= (n-1)/2.
П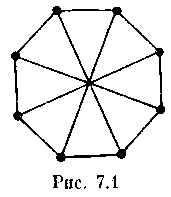 усть
Zn
— аддитивная группа классов целых чисел
по
модулю n,
AZn,
0A
и
для xA
класс
–x
также
принадлежит множеству A.
Определим
граф G
порядка
n
c
множеством вершин Zn
следующим
условием: вершины
x
и
y
смежны,
если x
— yA.
Очевидно,
что граф
G
регулярен
и степень его равна |A|.
Остается
доказать,
что для любого числа d,
удовлетворяющего
указанным выше условиям, существует
подходящее d-элементное
множество A.
При
d
= 2k
можно
взять A
=
{±1, ±2, ..., ±k},
а
при d=
2k+1
оказывается
четным
n,
и
можно взять A
={±1,
±2,
..., ±k,
n/2}
(см. рис.
7.1, где n
= 8, d
= 3). <
усть
Zn
— аддитивная группа классов целых чисел
по
модулю n,
AZn,
0A
и
для xA
класс
–x
также
принадлежит множеству A.
Определим
граф G
порядка
n
c
множеством вершин Zn
следующим
условием: вершины
x
и
y
смежны,
если x
— yA.
Очевидно,
что граф
G
регулярен
и степень его равна |A|.
Остается
доказать,
что для любого числа d,
удовлетворяющего
указанным выше условиям, существует
подходящее d-элементное
множество A.
При
d
= 2k
можно
взять A
=
{±1, ±2, ..., ±k},
а
при d=
2k+1
оказывается
четным
n,
и
можно взять A
={±1,
±2,
..., ±k,
n/2}
(см. рис.
7.1, где n
= 8, d
= 3). <
Утверждение 7.2. Если G = (X, Y, E)—непустой регулярный двудольный граф, то |X| = |Y|.
> Так как доле X принадлежит только один из концов каждого ребра графа G, то число m его ребер равно |Х| deg G. Аналогично m = |Y| deg G. Следовательно, |X| deg G = |Y| deg G. Поскольку deg G0, то |X|= |Y|.<
Иногда, хотя и редко, граф определяется степенями своих вершин. Например, только On является регулярным графом порядка n нулевой степени. Регулярный граф первой степени имеет четный порядок 2т и является дизъюнктным объединением m ребер. Этот граф обозначается символом тK2. Все связные компоненты регулярного графа второй степени являются простыми циклами. Однако уже кубические графы, т. е. регулярные графы степени 3, устроены сложно и не определяются степенями своих вершин. Примером кубического графа является граф Петерсена (рис. 1.6). Отметим любопытное свойство спектра регулярного графа.
Теорема 7.3. Пусть G — регулярный граф степени d. Тогда:
число d является корнем характеристического полинома графа G;
если G — связный граф, то кратность корня d равна 1;
d>= || для любого корня характеристического полинома графа G.
> 1) Пусть VG = {1, 2, ..., n}, A(G) = A — матрица смежности графа G, u—столбец высоты n, все элементы которого равны 1. Поскольку в каждой строке матрицы A ровно d единиц, то Au = du и, следовательно, u — собственный вектор, а d — собственное значение линейного оператора A. Но каждое собственное значение является корнем характеристического полинома. Тем самым доказано, что d — корень характеристического полинома графа G.
2) Для произвольного собственного вектора x = (x1, x2, . . ., xn) с собственным значением d имеем
Ax = dx x0. (1)
Пусть xj — координата вектора x с максимальным модулем, Nj = N(j) –окружение вершины j в графе G. Из равенства (1) для j-й координаты вектора Ax вытекает
и![]() ,
далее,
,
далее,
![]() (3)
(3)
Поскольку |Nj| = d, то из соотношений (2) и (3) следует, что xi = xj для всех i из Nj.. Для связного графа G теперь получаем, что все координаты вектора x равны между собой, т. е. размерность подпространства собственных векторов линейного оператора A, относящихся к собственному значению d, равна 1. Следовательно, и кратность корня d характеристического полинома матрицы A равна 1.
3![]() )
Пусть
— произвольный корень характеристического
полинома матрицы A,
x
—
соответствующий собственный
вектор. Тогда Ах
=
х,
и
в тех же обозначениях,
что и выше, имеем
)
Пусть
— произвольный корень характеристического
полинома матрицы A,
x
—
соответствующий собственный
вектор. Тогда Ах
=
х,
и
в тех же обозначениях,
что и выше, имеем
откуда || <= d. <
