
- •Глава I
- •§ 1. Определение графа
- •§ 2. Подграфы
- •§ 3. Операции над графами
- •§ 4. Цепи, циклы, компоненты
- •§ 5. Степени вершин графа
- •§ 6. Матрицы, ассоциированные с графом
- •§ 7. Регулярные графы
- •§ 8. Метрические характеристики графа
- •§ 9. Критерий двудольности графа
- •§10. Реберный граф
- •§ 11. Группа автоморфизмов графа
- •§ 12. «Почти все» графы
- •Упражнения
- •Глава II Деревья
- •§ 13. Определение дерева
- •§ 14. Матричная теорема Кирхгофа
- •§ 15. Остов минимального веса
- •Упражнения
- •Глава III
- •§ 16. Азбука теории матроидов
- •§ 17. Двойственный матроид
- •§ 18. Примеры матроидов
- •§ 19. Изоморфизм матроидов
- •§ 20. Представление матроида
- •§ 21. Бинарные матроиды
- •§ 22. Трансверсали
- •§ 23. Жадный алгоритм
- •§ 24. Объединение и пересечение матроидов
- •Глава IV Независимость и покрытия
- •§ 25. Независимые множества и покрытия
- •К. Шеннон ввел параметр
- •§ 26. Клика
- •§ 27. Проблемы клики, изоморфной вложимости и изоморфного подграфа
- •§ 28. Интерпретации независимых множеств
- •§ 29. Паросочетания
- •§ 30. Паросочетания в двудольном графе
- •§ 31. Двудольные графы и семейства подмножеств
- •§ 32. Паросочетания и покрытия
- •Упражнения
- •Глава V
- •§ 33. Вершинная связность и реберная связность
- •Чтобы учесть эту и подобные ей ситуации, естественно ввести следующее распределение: максимальный k-связный подграф графа называется его k-связной компонентой, или просто k-компонентой.
- •§ 34. Двусвязные графы
- •§ 35. Теорема Менгера
§ 32. Паросочетания и покрытия
Как отмечалось в § 25, определение числа βo(G) и, тем более, построение наименьшего вершинного покрытия для произвольного графа G — сложные алгоритмические задачи. Эффективных алгоритмов для их решения, видимо, не существует.
Очевидно, что для каждого графа G числа вершин в любом покрытии не меньше числа ребер в произвольном паросочетании, в частности,
![]()
Последние два числа могут как совпадать, так и не совпадать. Например, βo (К3)=2 α1(К3)=1. Для двудольного же графа эти числа всегда равны, т.е. верна следующая
Теорема 32.1. Для любого двудольного графа G число вершин в наименьшем вершинном покрытии равно
П![]() усть
G
= (X,
У, Е) — двудольный граф. Вначале редположим,
что в G
нет изолированных вершин. Очевидно,
что для любого подмножества А лежит X
множество
является покрытием графа G.
С другой стороны, пусть D
— произвольное минимальное покрытие.
Представим множество
D
в виде
усть
G
= (X,
У, Е) — двудольный граф. Вначале редположим,
что в G
нет изолированных вершин. Очевидно,
что для любого подмножества А лежит X
множество
является покрытием графа G.
С другой стороны, пусть D
— произвольное минимальное покрытие.
Представим множество
D
в виде
![]()
и![]() положим А =Х\Х1.
Тогда N(A)Y1.
Но как замечено выше,
множество Х1
U
N(A)
само является покрытием. Поскольку
покрытие D
минимально, то D
= Х1
U
N
(А). Итак,
всякое минимальное покрытие графа G
имеет вид (1),
и потому
положим А =Х\Х1.
Тогда N(A)Y1.
Но как замечено выше,
множество Х1
U
N(A)
само является покрытием. Поскольку
покрытие D
минимально, то D
= Х1
U
N
(А). Итак,
всякое минимальное покрытие графа G
имеет вид (1),
и потому
Д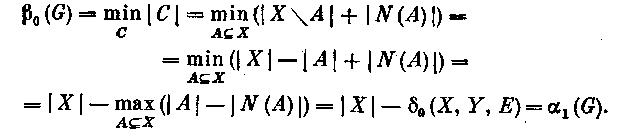 ля
графов без изолированных вершин теорема
доказана.
ля
графов без изолированных вершин теорема
доказана.
Очевидно, что при добавлении к графу G изолированной вершины не меняется ни βo(G), ни a1>(G), так что теорема верна и для графов с изолированными вершинами. Поскольку для любого графа G верны равенства a0(G)+ βo(G)=\G\ (теорема 25.5) и α1(G)+ β1(G)= \G\ (теорема 29.1), то из теоремы 32.1 вытекает
Следствие 32.2 (Д. Кёниг, 1916). Для любого двудольного графа G верны равенства
![]()
Как показано в § 77, для построения наибольшего паросочетания и наименьшего вершинного покрытия в двудольном графе существуют эффективные алгоритмы. Следовательно, и сложнейшая в общей ситуации задача нахождения наибольшего независимого множества в классе двудольных графов решается эффективно.
Как следствие из теоремы 32.1 получим один важный факт из теории бинарных матриц, доказанный Д. Кёнигом в 1931 году. Под линией матрицы будем понимать ее строку или столбец. Два элемента матрицы назовем независимыми, если они не лежат на одной линии.
Теорема К ё н и г а. Максимальное число попарно независимых единиц бинарной матрицы равно минимальному числу ее линий, содержащих все единицы матрицы.
С одной стороны, произвольная бинарная матрица А может истолковываться как приведенная матрица смежности некоторого двудольного графа G =(Х, Y, Е). Тогда независимость двух единиц матрицы означает, что соответствующая им пара ребер графа G несмежна. Поэтому максимальное число независимых единиц матрицы А равно числу паросочетания a1(G).
С другой стороны, каждой строке матрицы А соответствует вершина из X, каждому столбцу — вершина из У, а единицам линии — ребра, инцидентные соответствующим вершинам. При этом множеству линий матрицы А, содержащих все ее единицы, соответствует множество вершин графа G, являющееся покрытием. Следовательно, минимальное число элементов в покрытиях графа G равно минимальному количеству линий матрицы А, содержащих все ее единицы. Но согласно теореме 32.1 число вершин в наименьшем покрытии графа G также равно α1(G)
