§ 30. Паросочетания в двудольном графе

При изучении паросочетаний основное внимание будет уделяться двудольным графам. Для поиска паросочетаний в произвольном графе используются те же идеи, что в случае двудольных, только реализация их усложняется.

Самые разные задачи связаны с построением паросочетаний в двудольных графах. Приведем только два примера. Первый из них — задача о свадьбах, упоминавшаяся

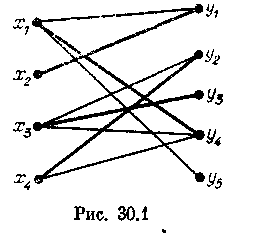
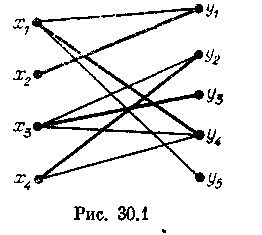
в § 22 в связи с теорией трансверсалей. Существование решения этой задачи равносильно существованию специально построенном двудольном графе (X, Y, Е) паросочетания, покрывающего X. В этом графе вершины из X соответствуют юношам, изY — девушкам, а ребро соединяет вершины, соответствующие знакомым юноше и девушке. На рис. 30.1 изображен граф для задачи о свадьбах, заданной таблицей 22.1. Жирными линиями выделены ребра паросочетания, решающего задачу.

Второй пример — задача о назначениях. Имеется конечное множество исполнителей {х₁, x₂, ..., х_n}, каждый из которых может выполнять некоторые из ра-

бот {y₁, y₂, ...,y_n). Стоимость выполнения работ y_i исполнителем xj равна w_ij. Нужно распределить исполнителей по работам, т. е. назначить по одному исполнителю на каждую работу, так, чтобы, во-первых, выполнить все работы и, во-вторых, минимизировать общие затраты. Как и в случае задачи о свадьбах, строится двудольный граф, каждому ребру которого приписывается вес, равный стоимости выполнения исполнителем соответствующей работы. Возможность выполнения всех работ равносильна существованию в графе совершенного паросочетания, а назначение, минимизирующее все затраты, соответствует

наибольшему паросочетанию с минимальным суммарным весом.

Рассмотрим условия существования паросочетаний. Для произвольного подмножества А в VG положим

Назовем N_G(A) окружением подмножества А в графе G.

Очевидно, что если для графа G = (X, У, Е) существует паросочетание, покрывающее X, то для любого подмножества А в X число вершин, смежных с элементами из А, не меньше, чем число вершин в А, т. е.

|N (A)|>|A|

Оказывается, что это условие является и достаточным для существования такого паросочетания.

Теорема 30.1. Для существования в двудольном графе G = (X, Y, Е) паросочетания, покрывающего X, необходимо и достаточно, чтобы любое подмножество А множества X удовлетворяло условию

|A||N (A)|.

Ниже показано, что эта теорема является переформулированной теоремой Холла о трансверсалях и потому не нуждается в дополнительном доказательстве. Однако для того, чтобы сделать эту главу независимой от предыдущей, приведем прямое доказательство теоремы о паросочетаниях.

Доказательство теоремы 30.1. Необходимость утверждения теоремы очевидна.

Достаточность докажем индукцией. Пусть G =(X, Y, E) —двудольный граф с /X/=m>0, удовлетворяющий 1ловию теоремы. При n — 1 единственная вершина из X инцидентна хотя бы одному ребру, которое и является нужным паросочетанием.

Пусть n > 1 и теорема верна для графов, у которых |X|<m. Отдельно рассмотрим два возможных случая.

1. Для каждого собственного подмножества А в X верно строгое неравенство \A\<\N_G(A)\. Выберем в G произвольное ребро ху. Если G^/ = G — х — у, X^/ = Х\x, = Y\y, Е' = E\{xu, vу:u  Y, v  X), то (X^/, У^/, E') двудольный граф, X^/ = m — 1. Пусть А^/ — произвольное подмножество множества X'. Так как |А'| |N_G(A')|, из Y удалена только одна вершина, то |А'| |N_G/(A')|. индуктивному предположению в графе G' существует паросочетание М, покрывающее X'. Добавив к М ребро получим нужное паросочетание графа G.

2. В множестве X существует такое собственное под- множество а_о, что верно равенство

Пусть G' и G" — подграфы графа G, порожденные множествами вершин A₀N_G(Ao) и VG\(Ао U N_G(Ао)) соответственно. Рассмотрим подграф G'.Для любого подмножества AA₀ имеем N_G (A) = N_G' (А), и следовательно | А |  | n_g'(a) |. По индуктивному предположению в G' существует паросочетание, покрывающее А о.

Обратимся к подграфу G''. Для любого подмножества А  Х\Ао выполняются соотношения |А₀| + |А| = |А₀U A|<=|N_G(A₀UA)| =

= |N_G(A₀)| + |N_G''(A)|

и верно равенство (1). Следовательно, |А||N_G''(A)| и по индуктивному предположению в графе G" существует паросочетание, покрывающее Х\Ао. Объединяя это паросочетание с построенным выше, получим паросочетание в графе G, покрывающее X.

Следствие 30.2. В любом регулярном непустом двудольном графе существует совершенное паросочетание.

Пусть G = (X,Y, Е) — регулярный двудольный граф, deg G == m > О, A  X. Тогда число ребер, инцидентных вершинам из А, равно m|A|. Степени концов этих ребер все равны т, поэтому

|N(A)|m\A\m=|A|.

Согласно теореме 30.1 существует паросочетание, покрывающее X. Поскольку для регулярного двудольного графа G=(Х, У, Е) всегда |Х| = |У|, то в нем всякое паросочетание, покрывающее X, является совершенным.

Следствие 30.3. Регулярный двудольный граф ненулевой степени является реберно непересекающимся объединением 1-факторов.

Пусть G — регулярный двудольный граф степени m > 0. При m == 1 он является 1-фактором. Пусть m > 1. Согласно предыдущему следствию в G существует совершенное паросочетание M.G — М — регулярный двудольный граф степени т — 1. Проведя эту процедуру несколько раз, придем к объединению 1-факторов.

Заметим, что утверждение следствия 30.3 перестает быть верным, если не требовать двудольности графа. В частности, граф Петерсена (рис. 1.7) был впервые введен в качестве примера кубического графа, не являющегося объединением 1-факторов.

Следствие 30.4. Пусть G = (X, У, Е) — двудольный граф, t—натуральное число, t<=\X\. Для существования в графе G паросочетания мощности t необходимо и достаточно, чтобы любое подмножество A  X удовлетворяло условию

Построим новый двудольный граф G' =(X, Y', E'), добавив \Х\ — t новых вершин к доле Y и соединив ребром каждую из них с каждой вершиной из X. Очевидно, что существование в графе G паросочетания мощности t равносильно существованию в графе G' паросочетания, покрывающего X, для (чего должно выполняться условие

A |N_G'(A)|. Последнее равносильно условию (2), поскольку | N_G, (А) \ =

=| N_G (А) | + | X | — t.

Для полноты картины отметим без доказательства следующую теорему.

Теорема 30.5. В произвольном графе G совершенное паросочетание существует тогда и только тогда, когда для любого подмножества S VG верно неравенство |S| p_o(S), где p_o(S)—число компонент нечетного порядка графа

G — S.

Возвратимся к двудольным графам. Пусть G = = (X, Y, Е) — двудольный граф с непустыми долями. Для любого подмножества А  X положим

Величину

назовем дефицитом графа G=(X, Y, Е). Очевидно, что 0<=δ₀<=|X|.

Теорема 30.6. Для произвольного двудольного графа G = (X, Y, E) с непустыми долями верно равенство α1(G)= |X|- δ₀.

Перепишем неравенство (2) в виде

Согласно следствию 30.4 для существования паросочетания мощности t необходимо и достаточно, чтобы для каждого А Ј X выполнялось условие (3). При t=|X| — δ₀ имеем δ (А)< \Х\ — t = δ₀, и, следовательно, неравенство (3) верно. Поэтому граф G имеет паросочетание мощности |Х| — δ₀

Если же t = |Х| — δ₀ + 1, то неравенство (3) принимает вид δ(А)< |Х| — t = δ₀ — 1 и нарушается для тех подмножеств а_о, для (которых δ(Ао) = δ₀. Следовательно, граф G не содержит паросочетания мощности |Х| — δ₀+l.

В частности, при |Х| = |Y|

С ледствие 30.7.Для любого двудольного графа G = (X, F, Е) верно равенство

Для доказательства достаточно заметить, что каждая часть равенства (4) совпадает с a1(G).