§ 27. Проблемы клики, изоморфной вложимости и изоморфного подграфа

Пусть G и G' — два графа. Требуется установить, существует ли в графе G' подграф, изоморфный графу G. Эта проблема изоморфного подграфа является одной из труднейших алгоритмических проблем теории графов.

Другой вариант этой проблемы — проблема изоморфной вложимости: требуется установить, существует ли в графе G' порожденный подграф, изоморфный графу G. Проблема изоморфного подграфа превратится в проблему изоморфизма графов, если дополнительно положить \G\ = \G'\ и \EG\ = lEG'l. Аналогична проблема изоморфной вложимости превратится в проблему изоморфизма, если положить |G| = |G'|.

Проблему клики часто рассматривают в таком виде: заданы граф G и натуральное число с; установить, верно ли неравенство фи (G)c

Очевидно, что проблема клики является частным случаем как проблемы изоморфного подграфа, так и проблемы изоморфной вложимости: требуется установить, является ли полный граф К_с подграфом графа G. На самом деле эти три проблемы эквивалентны, т. е. и проблема изоморфной вложимости, и проблема изоморфного подграфа могут рассматриваться, в свою очередь, как частные случаи проблемы клики. Этот факт первым доказал Г. Визинг, использовав свою конструкцию модульного произведения графов. Удобнее рассматривать не само произведение Визинга, а дополнительный к нему граф, именно эта конструкция ниже названа модульным проведением.

Модульным произведением G<>G' графов G и G' называется граф, определяемый следующими условиями:

1. V(G <> G'} = VGx VG' — декартово произведение множеств VG и VG'

2. вершины (и, и'] и (v, v') графа G<>G' смежны тогда и только тогда, когда одновременно и  v, u'  v'

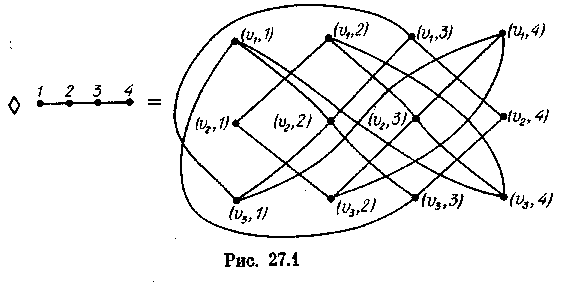
uv EG, uv' EG', либо uv EG, u'v' EG' рис. 27.1).

Теорема 27.1 (В. Г. Визинг, 1975 г.). Граф G изоморфно вкладывается в граф G' тогда и только тогда, когда γ(G<>G')>=|G|.

► Положим |G|=n. Пусть в графе G' существует . рожденный подграф G, изоморфный графу G, ψ VG->

VН — изоморфизм графов, VG = {1, 2, ..., n}, ψ(i) = vi= 1, n . Из определения модульного произведения непосредственно вытекает, что вершины (1, v₁), (2, v₂), ., (n, v_n) попарно смежны в графе G<>G' и, следовательно, ψ (G<>G')n.

Обратно, пусть ψ (G<>G')<>n, С — клика в графе: G<>G', содержащая ровно п верпшн. Тогда C = ((1, v₁), 2, V₂),....., (n,v_n)}, причем вершины v_i (i = l, n) n-паpнo различны. Положим H = G'(v₁, v₂,....., v_n). Очевидно, что соответствие i->v_i является изоморфизмом графов G и Н.

Заметим, что вершины (i, v_i) с равными одноименными координатами не смежны, поэтому γ (G <> G') n.

Следовательно, неравенство из формулировки предыдущей теоремы на самом деле является равенством.

Перейдем к проблеме изоморфного подграфа. Здесь требуется слегка изменить конструкцию модульного произведения.

Большим модульным произведением G<>G^r графов G и G' назовем граф, определяемый следующими условиями:

1. V(G<>G') = VGXVG',

2. вершины (u, и') и (v, v') графа G<>G' смежны тогда и только тогда, когда u v, и'v' и либо uv  EG, u'v EG', либо uv EG.

Теорема 27.2. В графе G есть подграф, изоморфный графу G, тогда и только тогда, когда γ (G <> G') = = |G|.

Доказательство аналогично доказательству предыдущей теоремы.