§ 2. Подграфы

Г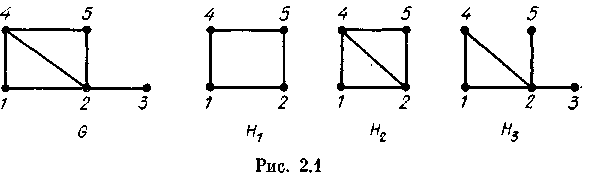 раф H называется подграфом (или частью) графа G, если VH VG, EH EG. Если H – подграф графа G, то говорят, что H содержится в G. Подграф H называется остовным подграфом (или фактором), если VH=VG. Если множество вершин подграфа H есть U, а множество его ребер совпадает с множеством всех ребер графа G, оба конца которых принадлежат U, то H называется подграфом, порожденным (или индуцированным) множеством U, и обозначается через G(U). На рис. 2.1 изображены граф G и три его подграфа H₁, H₂ и H₃, среди которых H₃ является остовным, a H₂ — порожденным.

Рассматриваются также подграфы, порожденные множествами ребер. Для E' EG множество ребер порожденного подграфа G(E') совпадает с E', а множество вершин — с множеством концов ребер из E'.

В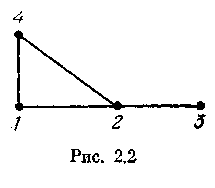 ажный класс подграфов составляют подграфы, полученные в результате удаления вершин. Пусть v — вершина графа G. Граф G_v = G — v получается из графа G в результате удаления вершины v и всех инцидентных ей ребер. Очевидно, что G_v = G(VG\v). На рис. 2.2 изображен подграф G — 5, полученный из графа G, представленного на рис. 2.1, удалением вершины 5.

С графами G_v связана знаменитая гипотеза реконструируемости Келли — Улама. Для каждой вершины v VG построим подграф G_v = G – v. Систему {G_v: v VG} всех таких подграфов назовем колодой графа G и обозначим через P(G). Например, если G = P₃, то P(G)= {K₂ , K₂ , O₂}.

Пусть |G|=n. Перенумеруем в произвольном порядке вершины графа G числами 1, 2, .... n и выпишем графы, входящие в колоду P(G):

P(G)={G₁, G₂, ..., G_n}, G_i=G-i, i=

Пусть теперь H — еще один граф порядка п. Если существует такая нумерация вершин графа H, при которой G_i H_i (i = ), то колоды P(G) и P(H) называются равными: P(G) = P(H). Например, P(K₂) = P(O₂) ={O₁,O₁}.

Граф H называется реконструкцией графа G, если P(H) = P(G).

Граф G называется реконструируемым, если он изоморфен каждой своей реконструкции. Не все графы реконструируемы: O₂ и K₂ являются реконструкциями друг друга. Гипотеза Келли — Улама утверждает, что это единственное исключение.

Гипотеза реконструируемости (П. Келли, С. Улам, 1945 г.). Все графы порядка n > 2 реконструируемы.

Несмотря на простоту формулировки, вот уже более сорока лет проблема не поддается решению. Любопытно и то, что нет единого мнения об истинности или ложности гипотезы. Подтверждена реконструируемость графов порядка n для 3 <= n<= 10. Известно, что если граф G реконструируем, то дополнительный граф также реконструируем.

Гипотезу Келли — Улама часто называют гипотезой вершинной реконструируемости. Наряду с ней для графов, имеющих более трех ребер, существует гипотеза Харари реберной реконструируемости (1964 г.). Она формулируется аналогично вершинной, но вместо вершины удаляется ребро: для ребра e графа G подграф G_e = G — e получается из G в результате удаления ребра e (концы ребра не удаляются, т. е. G — e является остовным подграфом). Гипотеза реберной реконструируемости подтверждена для многих классов графов. В частности, известно, что (n, т)-граф реберно реконструируем, если m>n(n-l)/4 (Л. Ловас, 1972 г.) или 2^m-l>n! (В. Мюллер, 1977 г.).

Пусть X — множество каких-либо элементов графа G. Аналогично подграфу G — v определяется подграф G — X: из G удаляются все вершины и ребра, входящие в X, и каждое ребро, хотя бы один конец которого принадлежит X. Если, например, X = {v, e₁, e₂}, то G — X = ( (G — v)— e₁) — e₂. Порядок удаляемых элементов несуществен, поэтому можно писать просто G — X = G — v — e₁ — e₂.