
- •Глава I
- •§ 1. Определение графа
- •§ 2. Подграфы
- •§ 3. Операции над графами
- •§ 4. Цепи, циклы, компоненты
- •§ 5. Степени вершин графа
- •§ 6. Матрицы, ассоциированные с графом
- •§ 7. Регулярные графы
- •§ 8. Метрические характеристики графа
- •§ 9. Критерий двудольности графа
- •§10. Реберный граф
- •§ 11. Группа автоморфизмов графа
- •§ 12. «Почти все» графы
- •Упражнения
- •Глава II Деревья
- •§ 13. Определение дерева
- •§ 14. Матричная теорема Кирхгофа
- •§ 15. Остов минимального веса
- •Упражнения
- •Глава III
- •§ 16. Азбука теории матроидов
- •§ 17. Двойственный матроид
- •§ 18. Примеры матроидов
- •§ 19. Изоморфизм матроидов
- •§ 20. Представление матроида
- •§ 21. Бинарные матроиды
- •§ 22. Трансверсали
- •§ 23. Жадный алгоритм
- •§ 24. Объединение и пересечение матроидов
- •Глава IV Независимость и покрытия
- •§ 25. Независимые множества и покрытия
- •К. Шеннон ввел параметр
- •§ 26. Клика
- •§ 27. Проблемы клики, изоморфной вложимости и изоморфного подграфа
- •§ 28. Интерпретации независимых множеств
- •§ 29. Паросочетания
- •§ 30. Паросочетания в двудольном графе
- •§ 31. Двудольные графы и семейства подмножеств
- •§ 32. Паросочетания и покрытия
- •Упражнения
- •Глава V
- •§ 33. Вершинная связность и реберная связность
- •Чтобы учесть эту и подобные ей ситуации, естественно ввести следующее распределение: максимальный k-связный подграф графа называется его k-связной компонентой, или просто k-компонентой.
- •§ 34. Двусвязные графы
- •§ 35. Теорема Менгера
Упражнения
1. Нарисуйте все попарно неизоморфные деревья седьмого порядка.
2. Найдите дерево минимального порядка n 2 с тождественной группой автоморфизмов.
3. Докажите, что центр дерева состоит из одной вершины в случае, когда диаметр этого дерева является четным числом, и из двух смежных вершин, когда диаметр — число нечетное.
4. Докажите, что радиус r(G) и диаметр d(G) любого дерева G связаны соотношением
r(G)=]d(G)/2.
5. Верно ли, что если диаметр связного графа G равен k (k > 2), то в G существует остовное дерево, диаметр которого так же равен k?
6.(n, m)-граф называется сбалансированным, если никакой его подграф не имеет вершин степени большей, чем 2т/n. Покажите, что всякое дерево при n > 2 — несбалансированный граф.
7.Найдите остовные деревья в К5, Кз,з и в графе Петерсена.
8.Докажите, что подграф H графа G является в G остовом тогда и только тогда, когда верны равенства \Н\ = \G\, m (H) = \G\-k(G), k(H)=k(G).
Используя матричную теорему Кирхгофа, найдите число остовных деревьев в полном двудольном графе Ктn.
Докажите, что число помеченных двудольных деревьев с числами вершин в долях т и n равно тn-1nт-1.
Покажите, как найти остов графа с помощью поиска в ширину.
Постройте такое множество U точек на плоскости, для которого вес дерева Штейнера был бы меньше веса любого остовного дерева графа K(U).
Глава III
Матроиды и трансверсали
В этой главе вводится новый комбинаторный объект — матроид, появляющийся в результате обобщения хорошо известного читателю понятия линейной зависимости. Хотя понятие «матроид» возникло относительно давно,— в 30-е годы нашего столетия (впервые это понятие ввел Уитни) — место теории матроидов в математике и, тем более, в математическом образовании первоначально не было осознано. Теперь же, когда открываются все новые и новые классы матроидов, объединяющая роль идеи матроида, позволяющая с возрастающим успехом применять к решению комбинаторных проблем методы алгебры, становится все более ясной.
Для нас матроиды интересны, прежде всего, по двум причинам. Первая — их связь с теорией графов. Фактически, именно соответствие между некоторыми теоретико-графовыми и алгебраическими понятиями привело к созданию теории матроидов. Вторая причина состоит в том, что задачи оптимизации на матроидных структурах решаются с помощью простого, так называемого «жадного» алгоритма, который является обобщением алгоритма Краскала для нахождения остовного дерева минимального веса в связном взвешенном графе (§ 15). «Жадный» алгоритм изучается в этой главе.
§ 16. Азбука теории матроидов
Известно несколько эквивалентных друг другу определений матроида. Эти определения различаются тем, что учитывают различные свойства независимости. Начнем с определения, основанного на свойствах максимальных независимых множеств – баз.
Матроидом М называется пара (E, β), где E— конечное непустое множество, а β (или β (М))—непустое множество его подмножеств (называемых базами), удовлетворяющее следующим двум условиям (аксиомы баз).
В.1. Никакая из баз не содержится в другой базе.
В.2.
Если
B1
и
B2
–
базы, то для любого элемента b
B1
существует
такой элемент с
из
В2,
что
(В1\b)
![]() с – также
база.
с – также
база.
Элементы множества Е называются элементами матроида М. Число |Е| называется порядком матроида М.
Понятие матроида является естественным обобщением понятия линейной независимости. А именно, если Е – конечная система векторов некоторого линейного пространства, содержащая ненулевой вектор, то в Е существует максимальная линейно независимая подсистема –база системы Е. Напомним, что все базы системы Е удовлетворяют аксиомам баз В.1 и В.2. Следовательно, всякая такая система вместе с ее базами является матроидом. Этот матроид называется векторным.
Очевидно, что в обозначениях аксиомы В.2 либо b B2 и тогда можно взять с = b, либо с В2\В1, иное противоречило бы аксиоме В.1. Поэтому совокупность аксиом В.1 и В.2 равносильна совокупности аксиом В.1 и
В`.2. Если В1, B2 β и b B1\B2, то в B2\B1 существует такой элемент с, что (B1\b)\ с β.
Утверждение 16.1. Все базы матроида равномощны.
> Пусть B1 и В2– базы, |В1| ≤ |В2| и В1 = {b1, b2,…, bρ}. Согласно аксиоме В.2 в базе В2 существует такой элемент c1, что
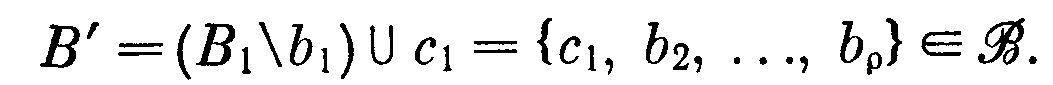
Далее, существует такой элемент с2 B2, что
![]() Итерируя
этот процесс, получим базу В
= (с1, с2, ...,
сρ),
являющуюся
подмножеством в В2
и
потому совпадающую
с В2
в
силу В.1. Следовательно, |В2|
=
ρ.
<
Итерируя
этот процесс, получим базу В
= (с1, с2, ...,
сρ),
являющуюся
подмножеством в В2
и
потому совпадающую
с В2
в
силу В.1. Следовательно, |В2|
=
ρ.
<
Мощность базы матроида М назовем его рангом и обозначим через ρ (М).
Любое подмножество базы матроида называется независимым. В частности, пустое множество независимо. Совокупность всех независимых подмножеств элементов матроида М обозначим через I(М) (или просто I). Ниже множество I(М) называется набором независимых множеств матроида М.
Очевидно, что β(М) совпадает с множеством элементов из I(M), максимальных относительно включения, так что множества β (М) и I (М) определяют друг друга.
Теорема 16.2. Набор I (М) независимых множеств матроида удовлетворяет следующим двум условиям (аксиомы независимости).
I.1. Если ХI(М), YX, то УI (М).
I`.2. Если X, YI (M) и |Х| < |Y|, то в Y\X существует такой элемент у, что X у I (M).
> Справедливость
условия 1.1 очевидна; рассмотрим условие
1.2. Пусть X,
YI
(M)
и
|Х|
<
|Y|.
Пусть,
далее,
B1
β
(M),
YB1.
Среди
баз, содержащих X,
выберем
такую базу В2,
чтобы
пересечение В1
∩
B2
содержало
наибольшее число элементов. Докажем,
что B2\XB1.
Действительно,
если бы существовал элемент b
В2\Х,
b![]() В1,
то
по аксиоме В.2 в базе В1
нашелся
бы такой элемент
z,
что C
= (B2\b)
В1,
то
по аксиоме В.2 в базе В1
нашелся
бы такой элемент
z,
что C
= (B2\b)
![]() z
β
(M).
Но
тогда |C∩B1|
>
|B2∩B1|,
что
невозможно. Следовательно, В2\Х
и
У содержатся
в В1,
причем
|В2\Х|
+ |Y|
=
ρ(М) — |X|
+ |Y|
>
ρ
(M)=|B1|.
Тем
самым существует у
(В2\Х)∩Y.
Поскольку
X
у
В2,
то
элемент у
–
искомый.
z
β
(M).
Но
тогда |C∩B1|
>
|B2∩B1|,
что
невозможно. Следовательно, В2\Х
и
У содержатся
в В1,
причем
|В2\Х|
+ |Y|
=
ρ(М) — |X|
+ |Y|
>
ρ
(M)=|B1|.
Тем
самым существует у
(В2\Х)∩Y.
Поскольку
X
у
В2,
то
элемент у
–
искомый.
Очевидно, что аксиома I.2 эквивалентна следующей аксиоме.
I`.2. Если X, YI (M) и |Х| < |Y|, то в Y существует такое подмножество Z, что X ZI (M), |X Z| = |Y|.
Следующая теорема показывает, что в основу определения матроида можно положить не базы, а независимые множества.
Теорема 16.3. Пусть Е — конечное непустое множество, I — непустая совокупность его подмножеств, удовлетворяющая аксиомам независимости I.1 и I.2, β — множество всех элементов из I, максимальных относительно включения. Тогда β удовлетворяет аксиомам баз В.1 и В.2.
> Очевидно, что β есть множество всех элементов из I максимальной мощности. Пусть теперь В1, В2 β, е1В1. Тогда B1\e1 I, |B1\e1| = |В2| - 1. Следовательно, существует такой элемент е2В2, что
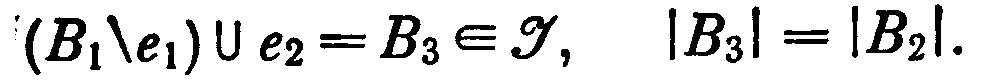 Из
последнего равенства вытекает, что B3
β.
Тем самым
доказано, что выполняется условие В.2.
Справедливость
условия В.1 очевидна. <
Из
последнего равенства вытекает, что B3
β.
Тем самым
доказано, что выполняется условие В.2.
Справедливость
условия В.1 очевидна. <
Предыдущая теорема дает основание для нового определения матроида. Матроидом назовем пару (Е, I), где Е — множество, а I — непустая совокупность его подмножеств (называемых независимыми), удовлетворяющих аксиомам независимости I.1 и I.2. Множество I назовем набором независимых множеств матроида. Максимальные относительно включения независимые подмножества назовем теперь базами матроида. Аксиомы баз при этом действительно будут выполняться. В этом смысле приведенные два определения матроида эквивалентны.
Определим ранговую функцию (функцию ранга) матроида М, ставящую в соответствие каждому подмножеству А Е число, равное максимальной из мощностей входящих в А независимых подмножеств и называемое рангом множества А: ρ (A) = max{|X|: ХА, ХI (М)}.
Очевидно, что ρ (E) совпадает с определенным выше рангом ρ(М). Очевидно также, что подмножество АЕ независимо тогда и только тогда, когда ρ(А)=|А|.
Теорема 16.4. Ранговая функция матроида удовлетворяет следующим трем условиям (аксиомы ранга):
 > Первые два
условия очевидны, рассмотрим третье.
Пусть
А,В
Е,
а
X
— наибольшее
по числу элементов независимое
подмножество в А
∩
В.
Согласно
условию I`.2
в
A
В
существует
наибольшее по числу элементов независимое
подмножество Y,
содержащее
X.
Представим
Y
в виде Y
= X
V
W,
где
VA\B,
WB\A.
Независимое
подмножество X
V
содержится
в А,
поэтому
ρ
(A)
≥ |Х
V|.
Аналогично
ρ
(B)
≥ |X
W|.
Следовательно,
ρ
(A)
+ ρ
(B)
≥ |X
W|
+|X
W|.
Поскольку
X∩V
= X∩W
= Ø, то
далее имеем ρ(А)
+ ρ
(В)
≥
|X|
+
(|X|
+
|V|
+ |W|).
Но
|Х|=
ρ
(A∩B),
|X|
+ |V|
+ |W|
=
|Y|=
ρ(A
В).
> Первые два
условия очевидны, рассмотрим третье.
Пусть
А,В
Е,
а
X
— наибольшее
по числу элементов независимое
подмножество в А
∩
В.
Согласно
условию I`.2
в
A
В
существует
наибольшее по числу элементов независимое
подмножество Y,
содержащее
X.
Представим
Y
в виде Y
= X
V
W,
где
VA\B,
WB\A.
Независимое
подмножество X
V
содержится
в А,
поэтому
ρ
(A)
≥ |Х
V|.
Аналогично
ρ
(B)
≥ |X
W|.
Следовательно,
ρ
(A)
+ ρ
(B)
≥ |X
W|
+|X
W|.
Поскольку
X∩V
= X∩W
= Ø, то
далее имеем ρ(А)
+ ρ
(В)
≥
|X|
+
(|X|
+
|V|
+ |W|).
Но
|Х|=
ρ
(A∩B),
|X|
+ |V|
+ |W|
=
|Y|=
ρ(A
В).
Итак, ρ (А) + ρ (В) ≥ ρ (A В) + ρ (А ∩ В). <
Подмножество А из Е называется зависимым, если оно не является независимым. Минимальное относительно включения зависимое множество называется циклом. Очевидно, что подмножество множества Е независимо тогда и только тогда, когда оно не содержит циклов.
Множество циклов матроида М обозначим через φ(М) (или просто φ).
Теорема 16.5. Если М — матроид, то множество φ(М) удовлетворяет следующим двум условиям (аксиомы циклов).
С.1. Ни один из циклов не содержится в другом цикле.
C.2. Если C1 и С2 — несовпадающие циклы и еС1 ∩ С2, то множество (С1 С2)\е также содержит цикл.
> Выполнимость условия С.1 очевидна, рассмотрим условие C.2. Пусть D = (C1 C2)\е. Достаточно доказать, что множество D зависимо. Прибегнем к помощи ранговой функции; в ее терминах нужно доказать неравенство ρ(D) ≤ |D|. Но D C1 C2, и потому ρ(D) ≤ ρ (C1 C2). Согласно аксиоме ρ.З
ρ (С1 С2) ≤ ρ (С1) + ρ (С2)- ρ (С1 ∩ С2).
Очевидно, что ρ (Ci)= |Ci| - 1 для цикла Ci. Так как множество С1 ∩ С2 независимо, то ρ(C1 ∩ С2)= |С1 ∩ С2|.
Итак,
ρ (D) ≤ ρ (C1 С2) ≤ |C1| - 1 + |С2| - 1 - |C1 ∩ С2| = |C1 С2| - 2
и |D| = |C1 С2| -1, а значит, ρ (D)< |D|. <
Заметим, что совокупность аксиом ρ.1 — ρ.З (как и C.1, C.2) можно использовать для еще одного определения матроида.
Следствие 16.6. Если М = (Е, I) — матроид с набором независимых множеств I, ХI, y Е, то множество X у содержит не более одного цикла.
> Пусть, напротив, в X у есть два несовпадающих цикла С1 и С2. Элемент у содержится в каждом из них, и, согласно предыдущей теореме, существует третий цикл С в множестве D = (C1 С2)\у. Следовательно, D — зависимое множество. Но DX и потому независимо. Полученное противоречие доказывает нужное утверждение. <
Очевидно, что из предыдущего следствия вытекает
Следствие 16.7. Для любой базы В матроида и любого его элемента е, не входящего в эту базу, множество В е содержит ровно один цикл.
