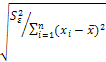- •Если каждому значению факторного признака соответствует вполне определенное неслучайное значение результативного признака
- •Линейные
- •Это наука, предметом изучения которой является количественное выражение взаимосвязей экономических явлений и процессов
- •Разработать способы моделирования и количественного анализа реальных экономических объектов
- •Постановочный, априорный, параметризации, информационный, идентификации, верификации
- •Построение эконометрических моделей с целью эмпирического анализа
- •Проверка качества как самой модели в целом, так и ее параметров
- •Спецификацией модели;
- •Математика, статистика, экономическая теория;
- •Наличие обратной корреляционной связи
- •Тесноту связи между двумя переменными при фиксированном значении остальных факторов
- •Зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков
- •На значимость коэффициентов регрессии
- •Обратную зависимость между X и y
- •Частного линейного коэффициента корреляции между y и x1
тесноту связи между двумя переменными
тесноту связи между тремя переменными
Тесноту связи между двумя переменными при фиксированном значении остальных факторов
Под частной корреляцией понимается:
зависимость результативного признака и двух и более факторных признаков, включенных в исследование
связь между двумя признаками (результативным и факторным или двумя факторными)
Зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков
зависимость между качественными признаками
Множественный линейный коэффициент корреляции R равен 0,75. Какой процент вариации зависимой переменной уi учтен в модели и обусловлен влиянием факторов х1 и х2:
56,2
75,0
37,5
0,75
Индекс корреляции определяется по формуле:
Какое значение может принимать множественный коэффициент корреляции:
1,501
-0,453
0,861
Приведенная
формула ![]() является:
является:
парным линейным коэффициентом корреляции
множественным коэффициентом детерминации
корреляционным отношением
парным коэффициентом детерминации
нет правильного ответа
Коэффициент детерминации указывает:
На значимость коэффициентов регрессии
на достоверность выбранной эконометрической модели
на наличие связи между зависимой и независимой переменными
на отсутствие связи между зависимой и независимой переменными
нет правильного ответа
Какой из парных линейных коэффициентов корреляции указывает на наибольшую тесноту связи?
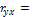 0,80
0,80
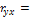 -0,45
-0,45 0,40
-0,85
Исследователь
получил следующее значение ![]() .
Это указывает на:
.
Это указывает на:
отсутствие зависимость x и y
Обратную зависимость между X и y
прямую зависимость между x и y
ошибку в расчетах
Исследователь
получил следующее значение ![]() .
Это указывает на:
.
Это указывает на:
отсутствие зависимость между показателями
обратную зависимость между показателями
прямую зависимость между показателями
ошибку в расчетах
Приведенная формула
![]() ,
предназначена для оценки:
,
предназначена для оценки:
Частного линейного коэффициента корреляции между y и x1
частного линейного коэффициента корреляции между y и x1
частного линейного коэффициента корреляции между y и x2
частного линейного коэффициента корреляции между x1 и x2
В результате
анализа взаимосвязи между показателями
Y
и X
были получены следующие промежуточные
значения ![]() .
Чему равен парный линейный коэффициент
корреляции Пирсона?
.
Чему равен парный линейный коэффициент
корреляции Пирсона?
2,46
0,40
0,79
-0,79
Если
![]() =
3341,1,
=
3341,1,
![]() =12,4,
=12,4,
![]() =226,8,
sx
= 1,2, sy=143,92
– чему равно значение парного линейного
коэффициента корреляции?
=226,8,
sx
= 1,2, sy=143,92
– чему равно значение парного линейного
коэффициента корреляции?
0,88
0,74
-0,88
Классическая линейная регрессия
Уравнение
множественной регрессии имеет вид: ![]() = -27,16 + 1,37х1
-
0,29х2.
Параметр а1
= 1,37 означает следующее:
= -27,16 + 1,37х1
-
0,29х2.
Параметр а1
= 1,37 означает следующее:
при увеличении х1, на одну единицу своего измерения переменная у увеличится на 1,37 единиц своего измерения
при увеличении х1, на одну единицу своего измерения и при фиксированном значении фактора х2, переменная у увеличится на 1,37 единиц своего измерения
при увеличении х1 на 1,37 единиц своего измерения и при фиксированном значении фактора х2 переменная у увеличится на одну единицу своего измерения
Значение параметра а1 в уравнении линейной парной регрессии определяется по формуле:
Согласно методу наименьших квадратов минимизируется следующее выражение:
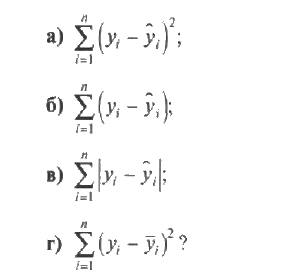 1
1
Оценки параметров регрессии (свойства оценок МНК) должны быть:
несмещенными
гетероскедатичными
эффективными
состоятельными
Значение бета-коэффициента определяется по формуле:
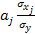 1
1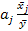
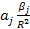
Чему
равен коэффициент эластичности, если
уравнение регрессии имеет вид
= 2,02 + 0,78x,
![]() 5,0
и
5,0
и ![]() 6,0:
6,0:
0,78
1,68
0,65
2,42
Какой коэффициент определяет среднее изменение результативного признака при изменении факторного признака на 1%:
коэффициент регрессии
коэффициент детерминации
коэффициент корреляции
коэффициент эластичности
Для нахождения параметров множественного регрессионного уравнения (А), при условии, что известны значения независимых переменных (Xj) и результатирующей переменной (Y) необходимо использовать следующую формулу:
А = (XTX)-1XTY;
А = (XX)-1XTY;
А = (XTX)XTY;
Нет правильного ответа.
Выберите уравнение регрессии, в котором связь между y и x обратная:
Значение параметра аj полученное меньше нуля указывает на:
прямую связь между показателями y и x
отсутствие связи между показателями y и x
обратную связь между показателями y и x
Предположим
оцениваем уравнение регрессии с двумя
независимыми переменными ![]() и
и ![]() ,
при этом b-коэффициент
при первом регрессоре получен равным
0,124, а при втором -0,673. Какой из регрессоров
оказывает наибольшее влияние на
результатирующую переменную:
,
при этом b-коэффициент
при первом регрессоре получен равным
0,124, а при втором -0,673. Какой из регрессоров
оказывает наибольшее влияние на
результатирующую переменную:
фактор
фактор
оба фактора
нельзя сопоставлять факторы
Допустим, получена следующая множественная модель в стандартизированном виде:
![]()
какой из факторов оказывает наибольшее влияние на результатирующую переменную:
фактор

фактор
оба фактора
нельзя сопоставлять факторы
Приведенная формула
![]() необходима для расчета:
необходима для расчета:
параметра уравнения
стандартизованным коэффициентом регрессии
коэффициента эластичности
По 15 промышленным
предприятиям рассматривается зависимость
прибыли от численности работников
предприятия и среднегодовой стоимости
основных средств, чему равно значение
фактическое F-критерия
Фишера при условии, что
![]() =30,949,
=30,949,
![]() =0,749:
=0,749:
249,597
32,125
0,187