Приложения определённого интеграла
1). Вычисление площадей плоских фигур.
Площадь
криволинейной трапеции, ограниченной
графиком функции
,
осью
,
прямыми
и
вычисляется по формуле
.
Если криволинейная трапеция расположена
ниже оси
(
),
то её площадь определяется так:
.Эти
формулы можно объединить в одну:
. (1)
Площадь
фигуры, ограниченной кривыми
и
,
прямыми
и
при условии
можно найти следующим образом:
. (2)
Если
кривая задана параметрическими
уравнениями
,
,
то площадь криволинейной трапеции,
ограниченной этой кривой, прямыми
,
и осью
,
выражается формулой
, (3)
где
и
определяются из равенств
и
[
при
].
Площадь
криволинейного сектора, ограниченного
кривой, заданной в полярных координатах
уравнением
и двумя лучами
,
(
),
вычисляется по формуле
. (4)
2). Вычисление длины дуги кривой.
Длина
кривой, являющейся графиком непрерывно
дифференцируемой функции
,
где
,
вычисляется по формуле:
. (5)
При
параметрическом задании кривой
,
[
и
– непрерывно дифференцируемые функции],
где
,
длина дуги находится по формуле
. (6)
Если
кривая задана уравнением
,
в полярных координатах, то длина дуги
равна
. (7)
3). Вычисление объёма тела.
Объём
тела, площади сечений которого плоскостями,
перпендикулярными оси
известны (
),
вычисляется по формуле:
. (8)
Если
вокруг оси
вращается криволинейная трапеция,
ограниченная непрерывной линией
,
отрезком
и прямыми
и
,
то объём тела вращения равен
.
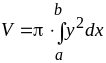Примеры решения задач
1.
Найти площадь фигуры, ограниченной
кривой
,
прямыми
,
,
.
Решение.
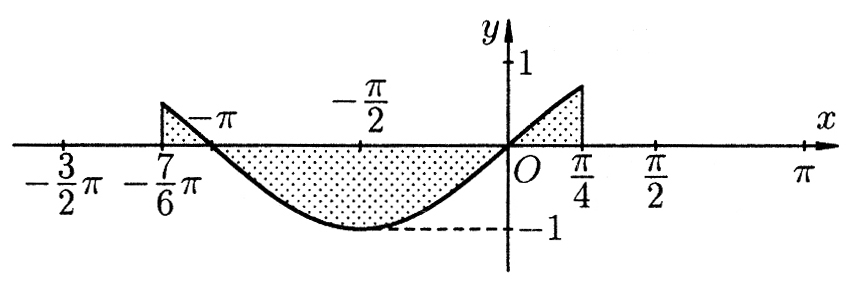
Фигура имеет вид, представленный на рис.1. Её площадь определяется по формуле (1):
.
Рис. 1. Рис. 2.
2.
Найти площадь фигуры, ограниченной
линиями
и
.
Решение.
Найдём абсциссы точек пересечения графиков данных функций. Для этого решаем систему уравнений
,
из
которой находим:
.
Искомую площадь (см. рис. 2) определяем
по формуле (2):
.
3.
Вычислить площадь плоской фигуры,
ограниченной одной аркой циклоиды (рис.
3) с уравнением
,
и осью
.
Решение.
Здесь
,
а
изменяется от
до
.
Следовательно, по формуле (3)
.
Рис. 3. Рис. 4.
4.
Найти площадь фигуры, ограниченной
лемнискатой
.
Решение.
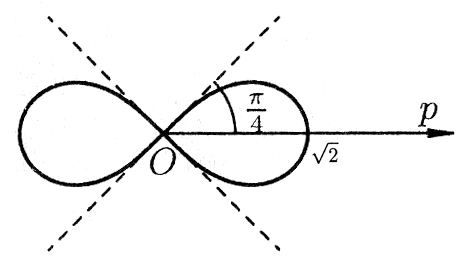
Четвёртой
части искомой площади (рис. 4) соответствует
изменение
от 0 до
.
По формуле (4) находим:
.
5.
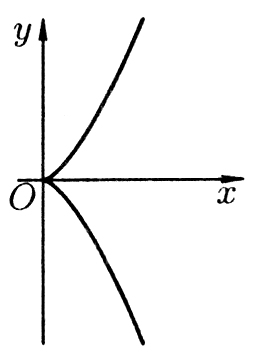
Вычислить длину дуги полукубической
параболы
(
)
от точки с абсциссой
до точки
.
Решение.
Здесь
.
Тогда
.
Тогда по формуле (5)
.
|
|
|
Рис. 5. Рис. 6. Рис. 7.
6.
Найти длину астроиды:
.
Решение.
,
.
Тогда
.
Теперь по формуле (6) с учётом симметрии линии (рис. 6) находим
.
7.
Найти длину кардиоиды:
.
Решение.
Сначала
найдём половину длины кривой, изображённой
на рис. 7, по формуле (7), учитывая, что
:
.
Значит,
.
8.
Найти объём эллипсоида
.
Решение.
Рассекая
эллипсоид (рис. 8) плоскостью, параллельной
плоскости
на расстоянии
от неё (
),
в сечении получим эллипс с уравнением
или
.
Площадь
этого эллипса равна
.
Поэтому, по формуле (8), имеем
.
|
|
Рис. 8. Рис. 9.
9.
Найти объём тела, образованного вращением
фигуры, ограниченной линиями
,
,
,
,
вокруг оси
.
Решение.
Для тела, изображённого на рис. 9, находим:
.
Задачи для самостоятельного решения
Найти площади фигур, ограниченных линиями:
1.
. Ответ:
.
2.
. Ответ:
.
3.
. Ответ:
.
4.
. Ответ:
.
5.
. Ответ:
.
6.
Эллипсом
. Ответ:
.
7.
Астроидой
. Ответ:
.
8.
. Ответ:
.
9.
. Ответ:
.
Найти длины дуг кривых:
1.
от вершины до точки с
. Ответ:
.
2.
до точки с абсциссой
. Ответ:
.
3.
от
до
. Ответ:
.
4.
Одной арки циклоиды
. Ответ:
.
5.
. Ответ:
.
6.
. Ответ:
.
7.
. Ответ:
.
Вычислить объёмы тел, ограниченных поверхностями:
1.
. Ответ:
.
2.
. Ответ:
.
Найти объём тела, образованного вращением фигуры, ограниченной линиями:
1.
вокруг оси
. Ответ:
.
2.
вокруг оси
. Ответ:
.
3.
вокруг оси
. Ответ:
.
4.
вокруг оси
. Ответ:
.
5.
вокруг оси
. Ответ:
.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 9