
- •Непосредственное интегрирование
- •Примеры решения задач
- •Метод замены переменной и формула интегрирования по частям
- •Примеры решения задач
- •Интегрирование рациональных дробей
- •Примеры решения задач
- •Интегрирование тригонометрических функций
- •Примеры решения задач
- •Интегрирование иррациональных функций
- •Примеры решения задач
- •Определённый интеграл
- •Примеры решения задач
- •Несобственные интегралы
- •Примеры решения задач
- •Приложения определённого интеграла
- •Примеры решения задач
- •Частные производные первого и высшего порядков. Дифференциал функции нескольких переменных.
- •Примеры решения задач
- •Производная сложной и неявно заданной функции нескольких переменных. Касательная плоскость и нормаль к поверхности
- •Примеры решения задач
- •Экстремум функции двух переменных
- •Примеры решения задач
- •Дифференциальные уравнения с разделяющимися переменными, однородные и сводящиеся к однородным уравнения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные уравнения первого порядка, уравнение Бернулли. Уравнение в полных дифференциалах
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Дифференциальные уравнения высших порядков. Уравнения, допускающие понижения порядка
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные однородные и неоднородные уравнения с постоянными коэффициентами, метод вариации постоянной
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные неоднородные уравнения с постоянными коэффициентами с правой частью специального вида
- •Примеры решения задач
- •Задачи для самостоятельного решения
Примеры решения задач
1.
Найти интегралы: а)
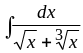 ;
б)
;
б)
 ;
в)
;
в)
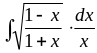 .
.
Решение.
Это интегралы типа 1.
а)
В этом случае
![]() .
Сделаем подстановку
.
Сделаем подстановку
![]() (6– наименьшее общее кратное чисел 2 и
3). Тогда
(6– наименьшее общее кратное чисел 2 и
3). Тогда
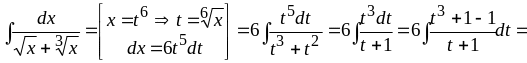

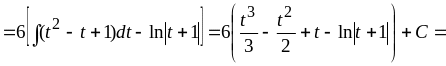
![]()
б)
В этом случае
![]() .
Сделаем подстановку
.
Сделаем подстановку
![]() (6– наименьшее общее кратное чисел 2 и
3). Тогда
(6– наименьшее общее кратное чисел 2 и
3). Тогда
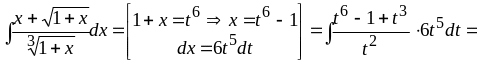
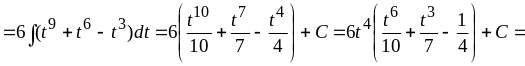
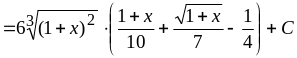 .
.
в)
В этом случае
![]() .
Сделаем подстановку
.
Сделаем подстановку
![]() .
Отсюда
.
Отсюда
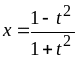 и, значит,
и, значит,
 .
.
Тогда


 .
.
2.
Найти интеграл
 .
.
Решение.
Это
интеграл типа 2. Применим подстановку
![]() .
Тогда
.
Тогда


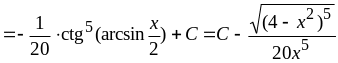 .
.
Здесь в последнем равенстве использована формула:
 .
.
3.
Найти интеграл
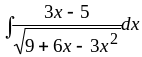 .
.
Решение.
Это интеграл типа 3. Выделим полный квадрат в знаменателе:
![]()
и
сделаем подстановку
![]() .
Тогда
.
Тогда



![]() .
.
4.
Найти интеграл
![]() .
.
Решение.
Представим
данный интеграл в виде
![]() .
.
Теперь
видно, что под знаком интеграла стоит
дифференциальный бином вида 4, при этом
![]() .
Так как в данном случае
.
Так как в данном случае
 –
целое число, то следует применить
подстановку 2), т. е.
–
целое число, то следует применить
подстановку 2), т. е.
![]() .
Следовательно,
.
Следовательно,
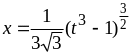 ,
и, значит,
,
и, значит,
 .
Таким образом,
.
Таким образом,


![]() .
.
Задачи для самостоятельного решения
1.
 Ответ:
Ответ:
 .
.
2.
 Ответ:
Ответ:
 .
.
3.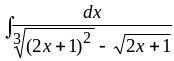 Ответ:
Ответ:
![]() .
.
4.
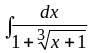 Ответ:
Ответ:
![]() .
.
5.
 Ответ:
Ответ:
 .
.
6.
 Ответ:
Ответ:
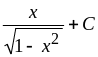 .
.
7.
 Ответ.
Ответ.
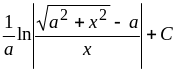 .
.
8.
 Ответ:
Ответ:
 .
.
9.
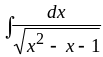 Ответ:
Ответ:
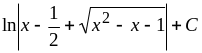 .
.
10.
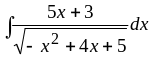 Ответ:
Ответ:
![]() .
.
11.
 Ответ:
Ответ:
 .
.
12.
![]() Ответ:
Ответ:
![]()
![]() .
.
13.
 Ответ:
Ответ:
 .
.
14.
 Ответ:
Ответ:

15.
 Ответ:
Ответ:
 .
.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 6
Определённый интеграл
Основные свойства определённого интеграла:
1.

2.
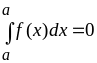
3.
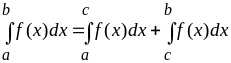
4.
 .
.
5.
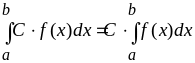 ,
где
– постоянная.
,
где
– постоянная.
6.
Оценка
определённого интеграла:
если
![]() на
на
![]() ,
то
,
то
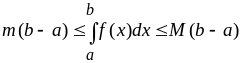
Правила вычисления определённых интегралов:
1. Формула Ньютона-Лейбница:
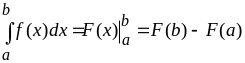 ,
,
где
– первообразная для
![]() ,
т. е.
,
т. е.
![]() .
.
2. Интегрирование по частям:
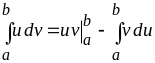 ,
,
где
![]() ,
,
![]() – непрерывно дифференцируемые функции
на отрезке
.
– непрерывно дифференцируемые функции
на отрезке
.
3. Замена переменной:
 ,
,
где
– функция, непрерывная на
,
– функция, непрерывная вместе со своей
производной на отрезке
![]() ,
,
![]() ,
,
![]() .
.
4.
Если
– нечётная функция, т. е.
![]() ,
то
,
то
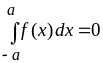 .
.
Если
– чётная функция, т. е.
![]() ,
то
,
то
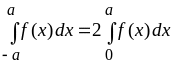 .
.
Примеры решения задач
Вычислить интегралы: а)
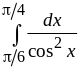 ;
б)
;
б)
 .
.
Решение.
а)
Подынтегральная функция
 на отрезке
на отрезке
 имеет первообразную
имеет первообразную
![]() .
Тогда по формуле Ньютона–Лейбница
.
Тогда по формуле Ньютона–Лейбница
 .
.
б) Выделяя полный квадрат в знаменателе под корнем, находим:
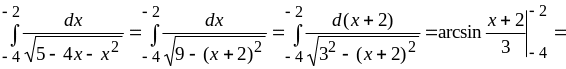
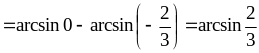 .
.
Оценить интеграл
 .
.
Решение.
Поскольку
![]() ,
имеем:
,
имеем:
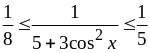 и
и
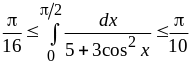 .
.
Вычислить интегралы: а)
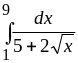 ;
б)
;
б) ;
в)
;
в)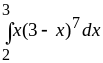 .
.
Решение.
Вычислим эти интегралы с помощью замены переменной.
а)
Применим подстановку
![]() .
Находим новые пределы интегрирования:
.
Находим новые пределы интегрирования:
-
1
9

1
3
Тогда
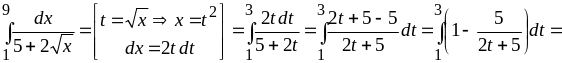
![]() .
.
б)

 .
.
в)

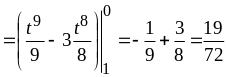 .
.
Вычислить интегралы: а)
 ;
б)
;
б)
 .
.
Решение.
Эти интегралы вычисляются с помощью формулы интегрирования по частям.
а)
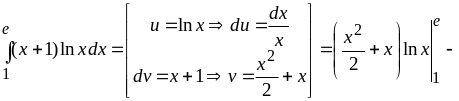
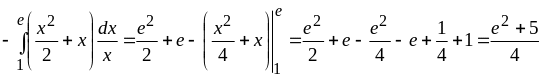
б)
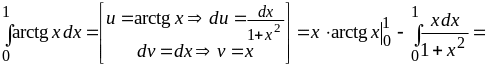
 .
.
Вычислить интегралы:
а) ;
б)
;
б)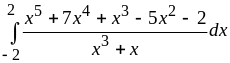 .
.
Решение.
Это интегралы в симметричных пределах. Значит, нужно проверить подынтегральные функции на предмет чётности-нечётности.
а)
Подынтегральная функция
 – нечётная, значит,
– нечётная, значит,
 .
.
б) В данном случае подынтегральная функция не является ни чётной, ни нечётной, но её можно представить в виде суммы таких функций:
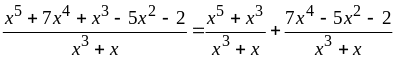 .
.
Тогда
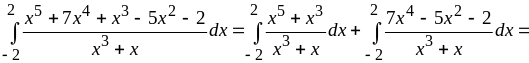
 .
.
Задачи для самостоятельного решения
1.
 Ответ:
Ответ:
![]() .
.
2.
 Ответ:
Ответ:
![]() .
.
3.
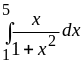 Ответ:
Ответ:
![]() .
.
4.
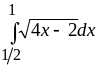 Ответ:
Ответ:
![]() .
.
5.
 Ответ:
Ответ:
![]() .
.
6.
 Ответ:
Ответ:
![]() .
.
7.
 Ответ:
Ответ:
![]() .
.
8.
 Ответ:
Ответ:
![]() .
.
9.
 Ответ:
Ответ:
![]() .
.
10.
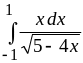 Ответ:
Ответ:
![]() .
.
11.
 Ответ:
Ответ:
![]() .
.
12. Ответ:
Ответ:
![]() .
.
13.
 Ответ:
Ответ:
![]() .
.
14.
 Ответ:
Ответ:
![]() .
.
15.
 Ответ:
Ответ:
![]() .
.
16.
 Ответ:
Ответ:
![]() .
.
17.
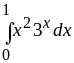 Ответ:
Ответ:
 .
.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 7
