Задачи для самостоятельного решения
1.
.
Ответ:
,
.
2.
,
.
Ответ:
.
3.
.
Ответ:
.
4.
.
Ответ:
arctg
.
5.
.
Ответ:
.
6.
.
Ответ:
.
7.
.
Ответ:
tg
.
8.
.
Ответ:
.
9.
.
Ответ:
.
10.
.
Ответ:
.
11.
.
Ответ:
.
12.
.
Ответ:
.
13.
.
Ответ:
.
14.
.
Ответ:
.
15.
.
Ответ:
.
16.
.
Ответ:
.
17.
.
Ответ:
.
18.
.
Ответ:
.
19.
.
Ответ:
.
20.
.
Ответ:
.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 13
Линейные уравнения первого порядка, уравнение Бернулли. Уравнение в полных дифференциалах
Линейным дифференциальным уравнением первого порядка называется уравнение
.
Если правая часть уравнения равна нулю, то это уравнение называется однородным, в противном случае – неоднородным.
Рассмотрим два метода интегрирования данного уравнения.
Метод
вариации постоянной. Находим
общее решение
однородного уравнения
.
Затем предполагаем, что
является функцией от переменной
,
и ищем решение неоднородного уравнения
в виде
.
Подставив его в неоднородное уравнение,
после некоторых преобразований, получим
дифференциальное уравнение с разделяющимися
переменными на неизвестную функцию
:
.
Его решением является
,
где
–
произвольное постоянное число. Общее
решение линейного уравнения запишется
в виде
.
Метод
подстановки (метод Бернулли).
Общее
решение неоднородного линейного
уравнения ищем в виде
,
тогда
.
Подставив
в уравнение, получим
,
или
.
Далее, пусть функция
удовлетворяет уравнению
,
тогда
.
Находим любое частное решение уравнения
,
например,
.
Тогда общим решением уравнения
будет
,
где
–
произвольное постоянное число. Общее
решение линейного уравнения имеет вид:
.
Уравнение вида
,
называется
уравнением
Бернулли. Если
обе его части разделить на функцию
и сделать замену
,
то получим линейное уравнение на
неизвестную функцию
.
Также уравнение Бернулли можно решать
методом подстановки.
Уравнение
называется
уравнением
в полных дифференциалах,
если его левая часть представляет собой
полный дифференциал некоторой функции
,
то есть это уравнение можно переписать
в виде
.
Отсюда общий интеграл будет
.
Для того чтобы уравнение
было уравнением в полных дифференциалах,
необходимо и достаточно выполнение
условия
.
Общий интеграл рассматриваемого
уравнения имеет вид
,
где
,
область
определения функций
.
Рассмотрим
еще один способ нахождения общего
решения уравнения в полных дифференциалах.
Так как с одной стороны
,
а с другой стороны
,
то отсюда следует, что функция
удовлетворяет условиям:
,
.
Примеры решения задач
1. Найти частное решение дифференциального уравнения
,
.
Решение. Будем решать уравнение методом вариации постоянной. Для этого составим соответствующее однородное уравнение
и
найдем его решение
.
Ищем решение исходного неоднородного
уравнения в виде
.
Вычислив
и подставив в заданное неоднородное
уравнение, получим дифференциальное
уравнение
,
решением которого является функция
,
где
–
произвольное постоянное число.
Следовательно, общее решение имеет вид
.
Используя начальное условие
,
найдем
,
отсюда частным решением будет
.
2. Найти общее решение дифференциального уравнения
.
Решение.
Переписав
уравнение
в
виде
,
заметим, что оно является линейным.
Решим его с помощью метода подстановки,
то есть ищем решение в виде
.
Подставив
и
в исходное уравнение, получим
.
Преобразуем последнее уравнение к виду
.
Найдем функцию
из условия
,
тогда
уравнение на функцию
будет следующим:
.
Решив
первое из двух последних уравнений,
получим одно из частных решений
.
Подставив найденную функцию
в последнее уравнение и проинтегрировав
его, получим
.
Следовательно, общим решением заданного
уравнения будет
.
3. Найти общее решение дифференциального уравнения
.
Решение.
Данное
уравнение не является линейным
относительно функции
,
но, переписав его в виде
,
или
,
видим,
что оно является линейным относительно
функции
.
Решим полученное уравнение методом
вариации постоянной. Составим
соответствующее однородное уравнение
,
разделим переменные
,
проинтегрируем
,
отсюда получим
.
Ищем общее решение неоднородного
уравнения в виде
.
Напомним,
что переменной является
.
Подставив последнее равенство в
неоднородное уравнение, после
преобразований получим уравнение на
неизвестную функцию
:
.
Его решением является
,
где
–
произвольное постоянное число. Таким
образом, получим ответ:
.
4. Найти общее решение дифференциального уравнения
.
Решение.
Это
уравнение Бернулли. Разделим обе части
уравнения на функцию
:
.
Введем замену
,
следовательно,
.
Тогда уравнение перепишется в виде
линейного уравнения
.
Его
решением будет
.
Отсюда
,
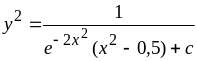или общий интеграл заданного уравнения имеет вид
.
Отметим, что заданное уравнение Бернулли можно также решить с помощью метода подстановки.
5. Найти частное решение дифференциального уравнения
.
Решение.
Это
уравнение Бернулли. Решим его методом
подстановки. Сделав замену
,
,
получим
,
или
.
Рассмотрим
два уравнения:
.
Интегрируем первое из них:
.
Подставляем найденную функцию во второе уравнение:
.
Разделяем переменные и интегрируем (в одном из интегралов используем метод интегрирования по частям):
,
отсюда
.
Тогда общее решение уравнения запишется
в виде
.
Используем
начальное условие
:
,
следовательно,
.
Таким образом, частным решением уравнения
будет
.
6. Найти общее решение дифференциального уравнения
.
Решение. Проверим, что это уравнение в полных дифференциалах:
и
.
Приведем
уравнение к виду
.
Для этого перепишем заданное уравнение
в виде
,
отсюда нетрудно заметить, что
.
Тогда уравнение примет вид:
,
следовательно, общим интегралом исходного уравнения является
.
7. Найти общее решение дифференциального уравнения
.
Решение. Проверим, что это уравнение в полных дифференциалах:
и
.
Воспользуемся
формулой
.
Пусть
и
,
так как данная точка входит в область
определения функций
.
Интегрируем (отметим, что при интегрировании по переменной x вторая переменная y считается постоянной):
.
Итак, общим интегралом заданного уравнения является
.
8. Найти общее решение дифференциального уравнения
.
Решение. Проверим, что это уравнение в полных дифференциалах:
и
,
Составим
систему
,
:
,
.
Проинтегрировав первое уравнение по переменной x (при этом переменную y считаем постоянным числом), получим
.
Подставив найденную функцию во второе уравнение, найдем
,
отсюда
,
следовательно,
.
Общим интегралом исходного уравнения будет , то есть
.