Исходные данные

ЗАДАНИЕ II B. Неравномерное движение воды и сопряжение бьефов за перепадом

В канале трапецеидального поперечного сечения устроен перепад (рисунок 1). В конце канала на стенке перепада устанавливается критическая глубина h_к.

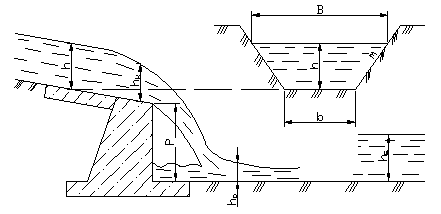
Рисунок 1 – Расчётная схема неравномерного движения воды на перепаде

Данные для расчета приведены в таблице 1.

Таблица 1

Q	b	i	P	hб	грунт
40	10	0.00047	1.64	1.22	глина

Q – расчетный расход воды, м³/с;

b – ширина канала по дну, м;

i – продольный уклон дна;

P – высота водослива и высота стенки перепада, м;

h_б –бытовая глубина, м;

1 Построение кривой свободной поверхности потока

1.1 Определение нормальной глубины наполнения

Определяем нормальную глубину наполнения h₀. Для этого рассчитываем модуль расхода по формуле:

.

Составляем таблицу 2, в которой задаемся рядом значений h и для каждого h вычисляем соответствующий модуль расхода К.

Таблица 2
h, м	, м2	, м	R, м	C,	K,
1	11,00	12,83	0,86	48,49	493,87
2	24,00	15,66	1,53	54,46	1618,21
3	39,00	18,49	2,11	58,05	3288,53
4	56,00	21,31	2,63	60,66	5505,90
2,157	26,22	16,10	1,63	55,12	1844,70

Определяем площадь поперечного сечения для данного русла:

ω = ,

где h – глубина наполнения канала, м;

b – ширина канала по дну, м;

m – коэффициент заложения откоса, для глины принимаем равным 1,

ω = м².

Определим длину смоченного периметра:

χ = ;

χ = м.

Определим гидравлический радиус:

R = ;

R = м.

Определим коэффициент Шези:

С = ,

где n – коэффициент шероховатости русла, n = 0.02;

y – коэффициент, зависящий от шероховатости и гидравлического радиуса русла, определяется по справочнику Киселева (таблица 3.10), у ≈ 0,2.

С = .

Определим модуль расхода водослива:

К = ;

К = .

По данным таблицы 2 строим график К = f(h), (рисунок 2)

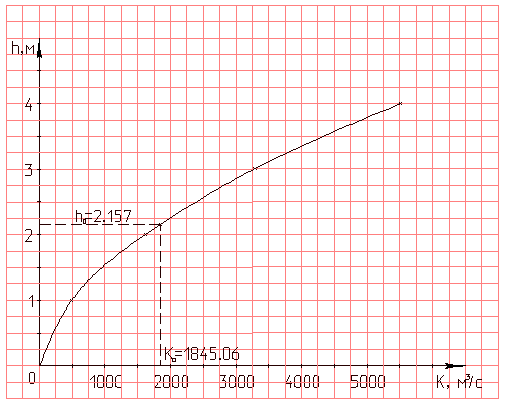
Рисунок 2 – График для определения нормальной глубины

По этому графику, зная К₀, находим искомую глубину. В таблице производим проверку правильности определения нормальной глубины.

Δ = % < 2 % => h₀ = 2.157 м.

1.2 Определение критической глубины

Определим коэффициент Кориолиса по формуле Г.В. Железнякова

α = ,

где g – ускорение силы тяжести;

С – коэффициент Шези.

α = .

Определим величину

м⁵.

Составляем таблицу 3, задаваясь значениями h, и вычисляем соответственно им величины .

Таблица 3
h, м	mh, м	(b+mh), м	ω, м2	ω3, м6	В = b + 2mh, м	ω3/В, м5
0,5	0,5	10,5	5,25	144,70	11	13,15
1	1	11	11	1331	12	110,92
1,5	1,5	11,5	17,25	5132,95	13	394,84
2	2	12	24	13824	14	987,43
контроль критической глубины hк
1,2	1,2	11,2	13,44	2427,72	12,40	195,78

По данным таблицы строим график h_к = f( ), (рисунок 3).

Рисунок 3 – График для определения критической глубины

По этому графику, зная , находим искомую глубину. В таблице производим проверку правильности определения критической глубины.

Δ = % < 2 % => h_к = 1.2 м.