Нелинейные системы

До сих пор мы рассматривали отклик систем, предполагая, что они являют­ся линейными. Но что произойдет, если эти системы нелинейны? На рис. 2.32 уже было показано, что по мере того, как входные величины становятся достаточно большими, всякая реальная система, в конце концов, становит­ся нелинейной из-за насыщения, перегрузки или ограничения. Сейчас на простом механическом примере мы проиллюстрируем, что происходит при этом с откликом.

Рассмотрим классический метод определения механической силы с по­мощью пружинного измерителя, в котором сила F_d, приложенная к внут­ренней пружине, преобразуется в пропорциональное изменение / длины пружины. Пусть штифт или кольцо, с помощью которых усилие передается пружине, обладают определенной массой, а о пружине предполагается, что у нее есть некоторое затухание. Тогда при малом входном воздействии, когда сила мала, и малом соответствующем изменении длины, можно воспользо­ваться аналогом, изображенным на рис. 2.42(b). Когда / мало, статическое поведение пружинного измерителя силы определяется законом Гука: F_d = К l, где K_t — жесткость пружины (ее коэффициент упругости). Динамическое поведение этой линейной системы уже рассмотрено: при малых нагрузках пружинный измеритель силы является линейной системой второго порядка «пружина с грузом» с демпфированием.

Однако в случае, когда прикладываемая сила велика, сказанное переста­ет быть справедливым: система становится нелинейной. Нелинейность воз­никает из-за того, что с увеличением растяжения или сжатия внутренняя пружина измерителя постепенно становится более жесткой или мягкой. Жесткость пружины больше не является постоянной. На рис. 2.46(a) показа­ны зависимости, иллюстрирующие статическое поведение такой нелиней­ной пружины.

Чтобы описать поведение пружинного измерителя силы более реалис­тично с учетом нелинейности, сделаем в линейном дифференциальном урав­нении второго порядка, относящемся к механической системе с поступа­тельным движением, подстановку: v = dl / dt. В результате получим:

и l =l(t).

Нелинейность возникает из-за четвертого слагаемого в левой части пер­вого из приведенных равенств. Предполагается, что нелинейность пружины симметрична (одинакова для растяжения и сжатия). Наличие нелинейности обусловлено тем, что степень l отлична от 1. Если > 0, то пружина стано­вится все более жесткой, по мере того, как она растягивается или сжимает­ся. Если = 0, то пружина линейна, а если

< 0, то она становится все менее упругой с ростом l. При очень малых значениях l система ведет себя как линейная система второго порядка, так как в этом случае

l < К l и поэтому членом l , ответственным за нелинейность, можно пренебречь.

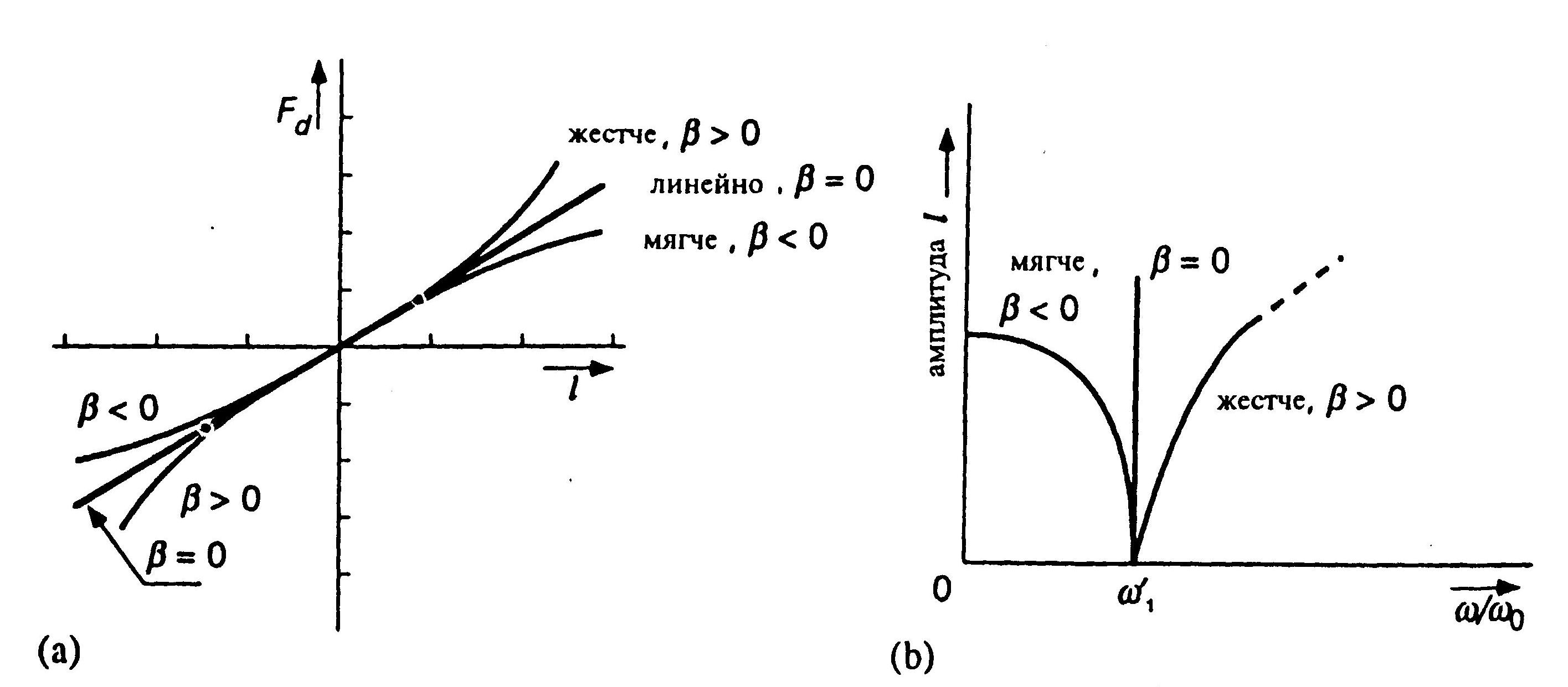
Рис.2.46. Нелинейная система «пружина с грузом», (а) Пружина, становящая­ся более жесткой,

> 0; линейная пружина, = 0; пружина, становящаяся более мягкой < 0; F — сила, необходимая для растяжения / сжатия пружи­ны на величину l. (b) Связь между амплитудой l основной гармоники свобод­ных колебаний нелинейной системы и нормированной резонансной частотой / .

Чтобы составить верное представление о динамическом поведении, рас­смотрим сначала свободные колебания системы: F_d(t) = 0 при t 0. Кроме того, предположим, что демпфирование отсутствует: D_t = 0. Однажды под­вергнутая воздействию, система будет продолжать колебаться, порождая периодический сигнал l = l(t) = l(t±nT), п — целое. Теперь период Т = 1/f = 2 / зависит от амплитуды колебаний! Это показано на рис. 2.46(b). При малых отклонениях частота со оказывается равной угловой частоте линейной системы второго порядка. По мере того, как амплитуда отклонений растет, период укорачивается или удлиняется в зависимости от того, стано­вится пружина более жесткой или менее жесткой ( > 0 или < 0). Следует заметить, что теперь колебание l=l(t) уже не является чисто синусоидаль­ным, а помимо основной гармоники содержит гармоники высших порядков. Форма колебания также меняется с ростом амплитуды отклонений. Колеба­ние является синусоидальным только при очень малых отклонениях.

Из нашего рассмотрения следует, что в случае нелинейных систем нельзя говорить о частотной характеристике, так как поведение системы теперь зависит от амплитуды! Принцип суперпозиции более не действует, и, как мы увидим дальше, динамическое поведение таких систем может быть са­мым удивительным.

Предположим теперь, что затухание уже не равно нулю (D_t 0) и на систему действует синусоидальная внешняя возбуждающая сила F_d = F_d (t) с постоянной амплитудой . На рис. 2.47 показано, что случится с такой системой, если пружина постепенно становится более жесткой ( > 0). На этом графике приведена зависимость амплитуды l=l(t)основной гармо­ники от частоты возбуждения .

Чтобы построить эту зависимость, необходимо отфильтровать частоту основной гармоники, совпадающую с частотой прилагаемого извне сило­вого воздействия, из (искаженного) сигнала l(t) . Здесь мы приводим только амплитуду этой основной гармоники (линеаризированное поведение). Как видим, резонансная кривая больше не имеет того привычного вида, который характерен для линейной системы второго

Рис. 2.47. Зависимость амплитуды основной гармоники вынужденных колеба­ний нелинейной системы «пружина с грузом» от частоты синусоидального воздействия постоянной амплитуды при наличии демпфирования (в случае, когда жесткость пружины увеличивается).

порядка и показан на рис. 2.45(a). Она теперь наклонена в сторону более высоких частот; другими сло­вами, она теперь перекошена. Если амплитуда синусоидального воздей­ствия меняется, то пик резонансной кривой будет перемещаться по штри­ховой линии, которая является характеристикой свободных колебаний (как на рис. 2.46(b), > 0).

Если частота возбуждающей силы увеличивается, но амплитуда оста­ется постоянной, то выходная величина в системе «пружина с грузом» вне­запно падает до много меньшего уровня (явление перескока) после того, как на частоте со = Ьсо₀ достигается пик резонансной кривой. Когда частота умень­шается (опять же при неизменной амплитуде входного воздействия), амп­литуда основной гармоники в сигнале /(/) вдруг скачком переходит к боль­шему значению на частоте =a . Следовательно, в интервале частот b b система неустойчива. Установившийся режим никогда не может принадлежать кривой, изображенной точками внутри этого интервала. Мы видим, что резонансные кривые такого рода нелинейных механических си­стем обладают гистерезисом.

Если мы теперь вдобавок станем изменять амплитуду возбуждающей силы F_d(t), то получим резонансные кривые, представленные на рис. 2.48. На рис. 2.48(a) показаны характеристики системы «пружина с грузом» в случае, когда жесткость пружины постепенно увеличивается, а на рис. 2.48(b) — для случая, когда жесткость пружины уменьшается.

Р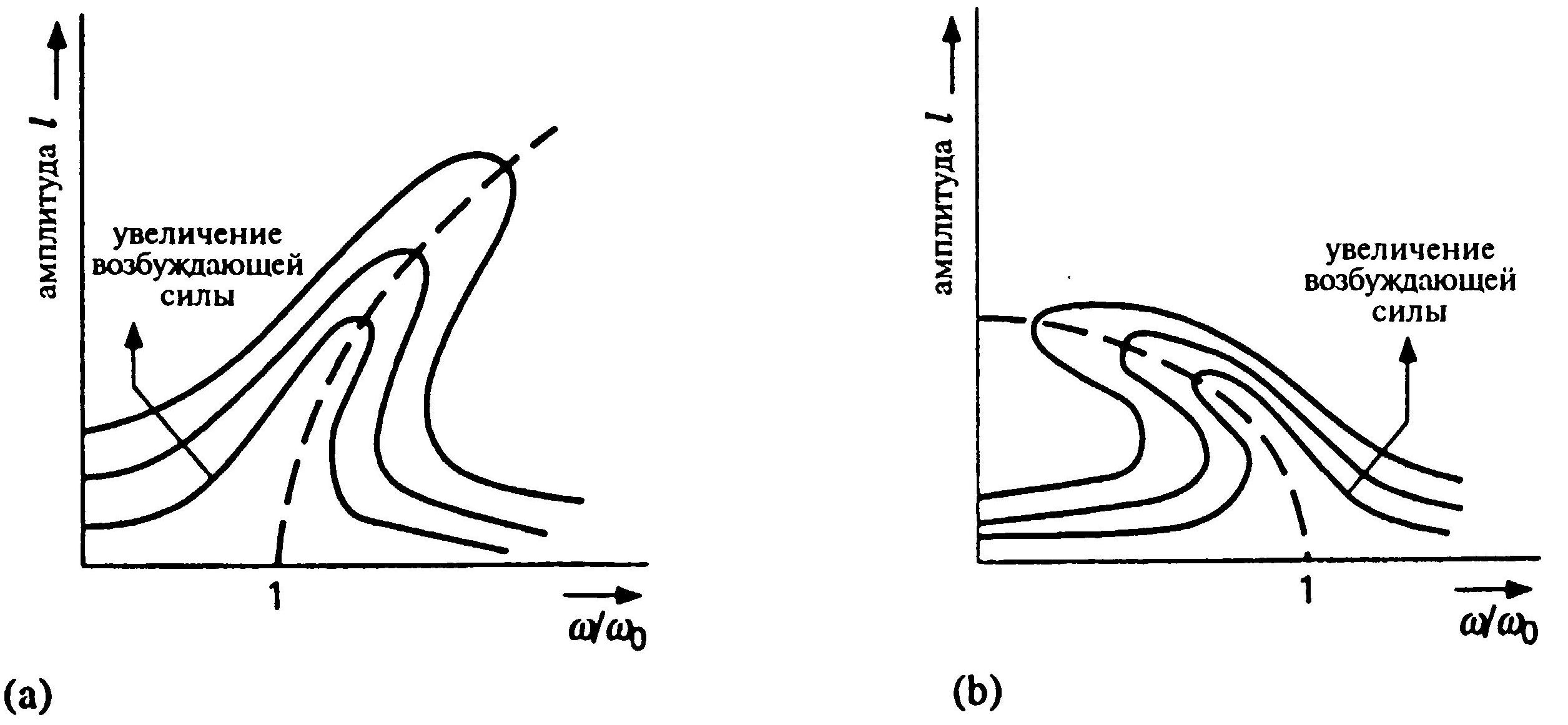 ис. 2.48. Влияние амплитуды входного воздействия на резонансные кривые (см. рис. 2.47) нелинейной системы «пружина с грузом» при наличии демпфи­рования. На рис. (а) представлен случай, когда жесткость пружины увеличива­ется (b > 0), а на рис. (b) показаны амплитудно-частотные характеристики для случая, когда пружина постепенно становится мягче (b < 0).

Наконец, обратим внимание на тот факт, что у систем такого рода при возбуждении их синусоидальным воздействием, помимо высших гармоник на частотах к , могут наблюдаться субгармоники на частотах / п (здесь к и п — целые числа). Обычно это происходит при малом, но не равном нулю затухании D_r.

Приведенный иллюстративный пример поведения нелинейной динами­ческой системы ясно показывает, насколько сложными могут быть эти сис­темы. Это обстоятельство является одной из причин, по которым в измери­тельных системах стараются избежать сколько-нибудь существенной (дина­мической) нелинейности: система становится слишком сложной.