2.41. Частотная характеристика системы первого порядка.

Системы второго порядка

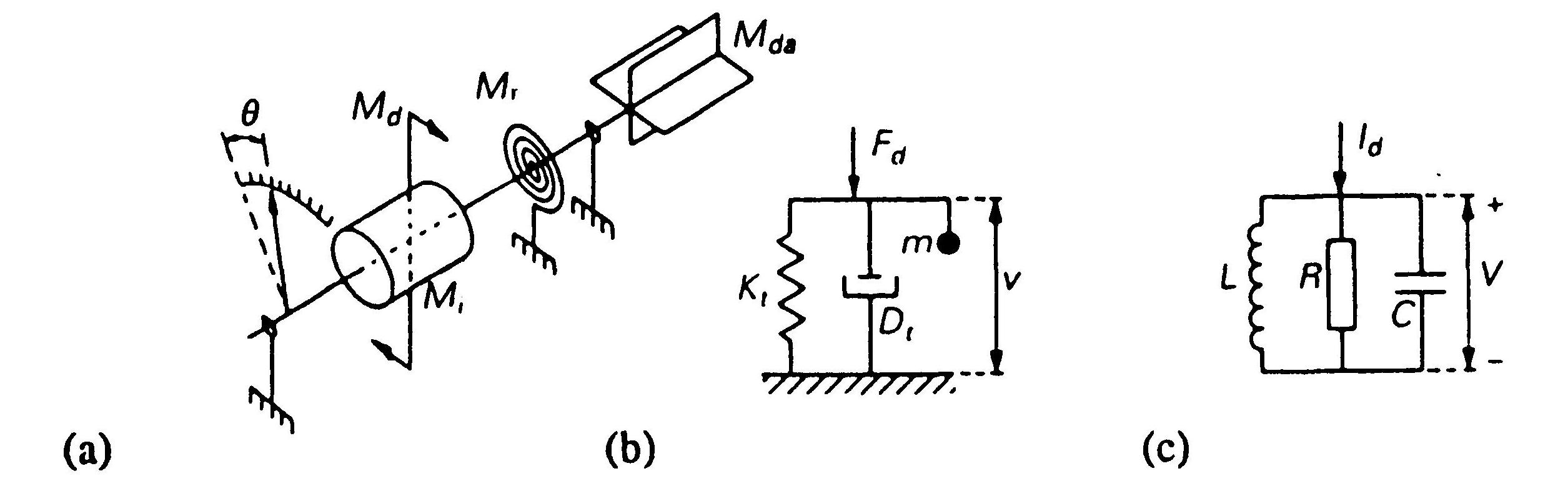
В качестве примера системы второго порядка мы воспользуемся конструк­цией стрелочного прибора (в частности, измерителя с подвижной катуш­кой), которая представляет собой вращающуюся механическую систему. Каждая из следующих четырех механических пар сил оказывает воздействие на вращающуюся часть измерителя, создавая вращающий момент (рис. 2.42(a)):

- Отклоняющее воздействие. Это воздействие вызывает отклонение стрел­ки на угол . Момент этого воздействия пропорционален измеряемой вели­чине (току). Мы обозначим этот момент M_d.

Рис. 2.42. Системы второго порядка: (а) механическое вращение; (b) механи­ческое поступательное движение; (с) параллельный электрический контур.

- Возвращающее воздействие. Это воздействие оказывает противодействие отклонению стрелки. В данном примере оно создается спиральной пружи­ной; вращающий момент этого воздействия обозначается М_r. Когда достига­ется установившееся состояние, отклоняющий момент и возвращающий момент равны: M_d = М_r. Обычно бывает так, что возвращающий момент пропорционален углу отклонения , то есть М_r = К_r , где К_r — коэффициент упругости (жесткость пружины).

- Демпфирующее воздействие. Это воздействие также противодействует отклоняющему моменту. Демпфирующий момент пропорционален угловой скорости стрелки, так что M_da = D_r d / dt. Здесь D_r — постоянная затухания вращающейся конструкции. Затухание линейно зависит от угловой скорости d / dt.

Демпфирование применяют для того, чтобы предотвратить проскакива-ние стрелки за конечное значение и колебания стрелки вокруг него. Для этого используют те или иные крыльчатые приспособления и поршни (воз­душное демпфирование), а также индукцию вихревых токов в металличес­кой пластине в случае движущихся систем (демпфирование за счет токов Фуко).

- Инерционность. Инерция вращающейся конструкции измерителя при­водит к возникновению еще одного противодействующего момента, кото­рый пропорционален угловому ускорению стрелки, так что

,

где J — момент инерции вращающейся конструкции относительно оси вращения.

Динамическое поведение измерителя определяется его уравнением дви­жения; в любой момент времени отклоняющий момент уравновешивается суммой всех других моментов:

M + M_da + М_r = M_d

или

.

В результате, как и следовало ожидать, мы пришли к линейному дифференциальному уравнению второго порядка.

Чтобы сделать более ясной аналогию с другими системами, указанными на рис. 2.42, перепишем полученное уравнение, введя новую переменную :

= M_d

Отклоняющий момент M_d является I-величиной (см. приложение А.4), а угловая скорость — V-величиной. Вращающаяся механическая система аналогична системе с поступательным движением, изображенной на рис. 2.42(b). Эта последняя состоит из груза массы т, пружины с коэффициен­том упругости K_t и демпфера с постоянной затухания D_t Если на систему действует сила F_d, то скорость v груза по отношению к земле удовлетворяет равенству

.

Поскольку v =dx / dt, мы снова приходим к тому же самому линейному дифференциальному уравнению второго порядка, что и полученное ранее. Наконец, обе механические системы — с вращательным и с поступатель­ным движениями — аналогичны электрической системе, показанной на рис. 2.42(c). На этот параллельный электрический контур действует I-величина: по нему течет ток I . Мы хотим определить V-величину, являющуюся реше­нием уравнения:

= I .

Это уравнение эквивалентно обоим уравнениям, полученным выше. Все различие может состоять в том, что I -величины и V-величины поменяются местами. Структура системы остается одной и той же, когда мы переходим от J к m или С, одновременно заменяя D_r на D_t или 1 / R, а также К_r - на K_t или 1 / L (см. приложение А.4). Принимая во внимание, что

V=L ,

последнее уравнение можно переписать в виде:

,

где I представляет собой ток, текущий по катушке L.

Мы видим теперь, что дифференциальное уравнение, описывающее ли­нейную систему второго порядка, в общем случае содержит две постоянные а и b:

.

Здесь х — это величина входного воздействия х(t), а у — выходная вели­чина y(t), нормализованная по отношению к чувствительности по постоян­ному току S(0), так что

у = y(f) / S(0). Благодаря нормализации третья посто­янная в дифференциальном уравнении отсутствует. Чтобы сделать запись более наглядной, введем две другие постоянные: относительное затухание z и угловую частоту свободных незатухающих колебаний в системе, и пере­пишем общее уравнение с использованием этих констант:

.

В случае системы с вращением переменные и параметры, входящие в это уравнение, имеют вид:

x= , y= , = и ,

а в случае системы с поступательным движением —

x= , y=x, = и ,

Для электрической цепи имеем:

X=I , y=I, = и ,

Соответствующее уравнение в операторной форме выглядит так:

,

и корни его равны

.

Необходимо различать следующие три характерных случая: z < 1, z = 1 и z>l.

Недостаточное демпфирование (z < 1)

Можно показать, что отклик системы y(t) на входной сигнал, имеющий форму скачка величины х₀ , происходящего в момент t = 0, равен

.

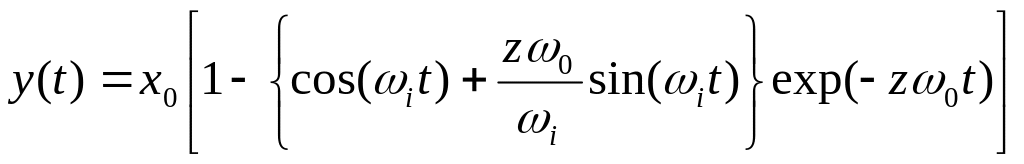где ; при выводе этого выражения предполагается, что на­чальные значения у(0) и (dy / dt)_t=0 равны нулю. Конечное значение, дости­гаемое в установившемся режиме, равно

.

Непосредственно вслед за входным скачком возникают затухающие ко­лебания с частотой , наложенные на конечное значение (см. рис. 2.43). Мы видим, что с ростом z затухание колебаний происходит все быстрее. Поэто­му z называют относительной скоростью затухания. Если z = 0, то колебания в системе продолжаются и их частота равна ; система находится в режиме свободных колебаний. Таким образом, — это резонансная частота системы, в которой затухание отсутствует полностью.

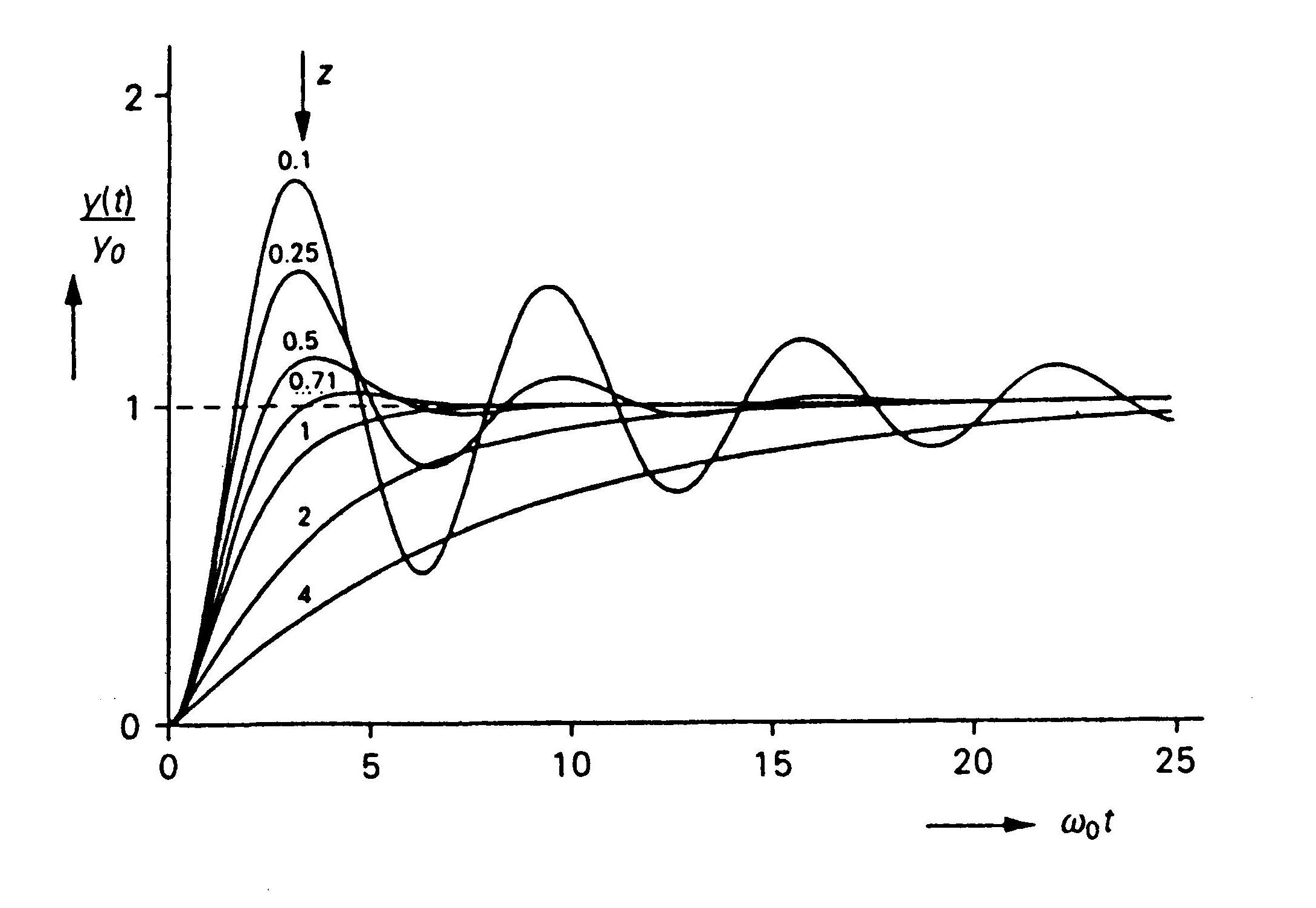
Рис. 2.43. Переходные характеристики системы второго порядка при различ­ных значениях относительного коэффициента затухания z.

Критическое демпфирование (z = 1)

Предполагая снова, что начальные условия являются нулевыми, то есть у(0) = 0 и (dy/dt) = 0, а величина скачка на входе в момент t = 0 равна х , получаем следующее выражение для переходной характеристики системы второго порядка при z = 1:

.

Как и ранее, конечное значение у₀ равно х₀, но теперь на выходе нет затухающих колебаний (см. рис. 2.43).

Обычно измерители с подвижной катушкой бывают сконструированы таким образом, чтобы демпфирование у них было не точно критическим, а слегка недостаточным (z = l/ ). Из-за этого происходит небольшое проскакивание стрелки (4%). Достоинство такого подхода состоит в том, что наблюдатель яснее видит, когда стрелка устанавливается на конечном зна­чении. У такого значения коэффициента затухания z применительно к изме­рительным системам есть и другое достоинство: при z 0,7 амплитудно-частотная характеристика оказывается горизонтальной в возможно более широком диапазоне частот (этот вопрос рассмотрен ниже; см. рис. 2.45).

Избыточное демпфирование) (z > 1)

При тех же начальных условиях, что и выше, но с коэффициентом зату­хания z больше единицы, переходная характеристика y(t) как реакция на входной скачок величины х₀ в момент t = 0 имеет вид:

,

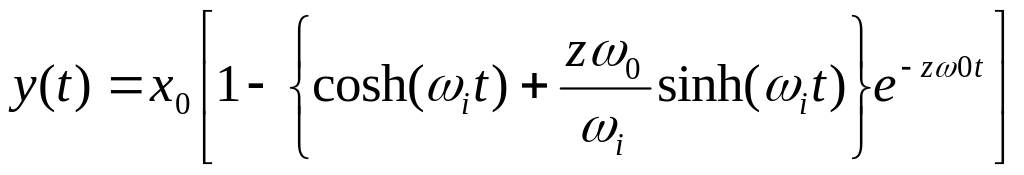где . В данном случае выходная величина будет постепенно приближаться («ползти») к конечному значению у₀ = х₀ (см. рис. 2.43).

Постоянная времени прибора или его время установления (готовности) t_s зависит от коэффициента затухания z, периода T₀, соответствующего час­тоте свободных колебаний (T₀ = 2 / ), и, естественно, от допустимой относительной ошибки в конечной величине y / y (см. рис. 2.44). У кривых на этом графике имеются разрывы при z < 1, обусловленные тем, что при заданных значениях Т₀ и относительной погрешности (скажем 0,1%) время готовности t_s увеличивается скачками при непрерывном уменьшении коэф­фициента затухания z. Причина скачков заключается в том, что время готов­ности каждый раз увеличивается на один период затухающих колебаний.

Частотную характеристику системы второго порядка легко найти, рас­сматривая RLC -аналог такой системы, показанный на рис. 2.42(c):

= .

Амплитудно-частотная характеристика имеет вид:

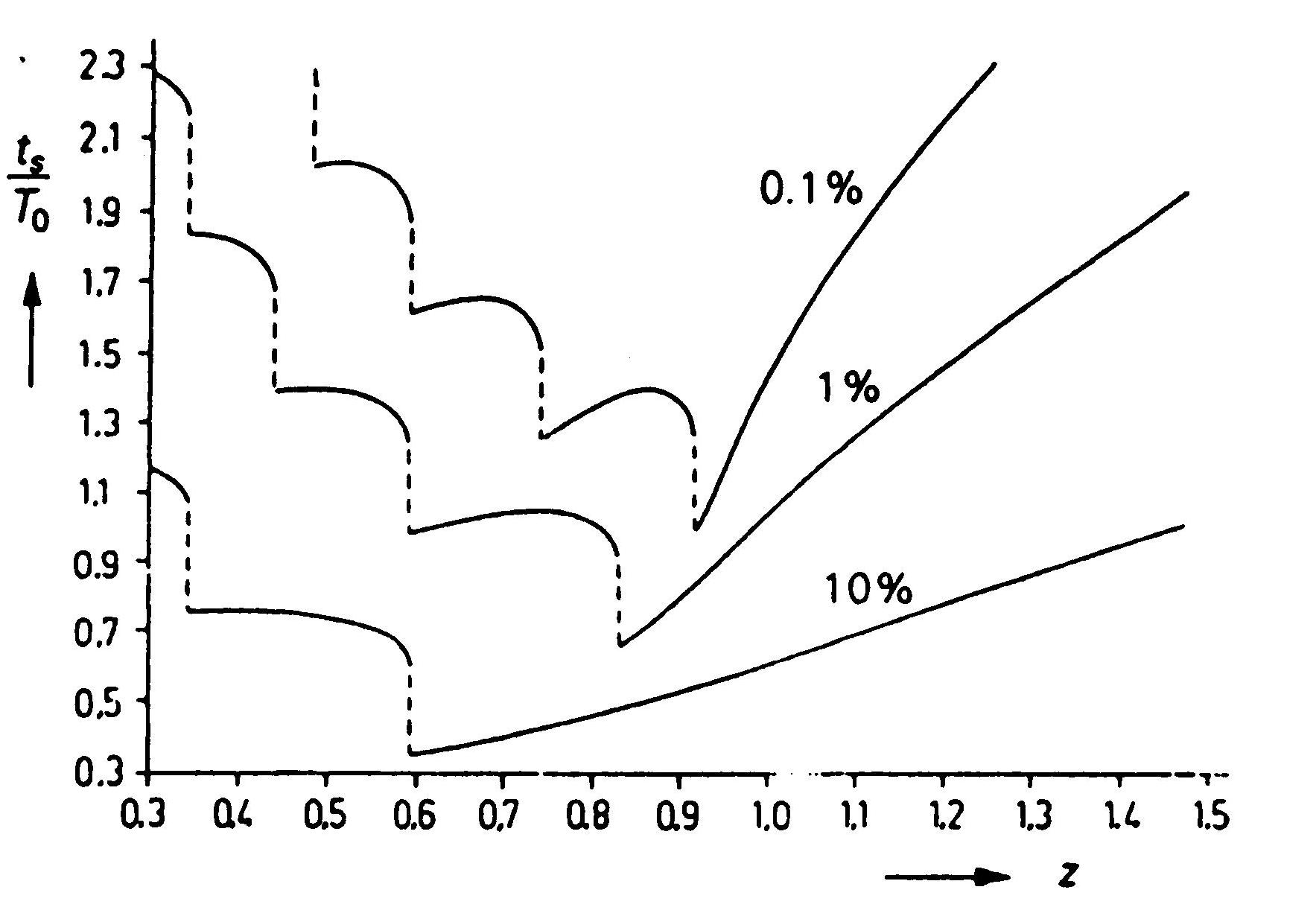
Рис.2.44. Время установления (готовности) t_s системы второго порядка при различных значениях допустимой относительной ошибки у₀ / у₀ в конечном результате y_Q. . T_Q — период свободных колебаний,,a z — относительный коэф­фициент затухания системы.

| |= ,

а для фазовой характеристики справедливо соотношение:

Arg = -arctg .

Подставляя z² = L/4R²C и =1 / LC , можно написать эти выражения в общей форме. Дифференцируя | | по , находим, что максимум | | достигается при

_тгх = и значение | | в максимуме равно

| |=

(при z ).

Частотная характеристика оказывается плоской в возможно более широ-ком диапазоне частот, если | | = | |=1, то есть в случае, когда z = /2. При этом ширина полосы системы равна f₀ = / 2 -, где t — частота свободных колебаний. В точке = фазовый сдвиг равен —90°. На очень высоких частотах сдвиг по фазе стремится к —180°, но никогда не превышает этого значения, а величина сигнала на выходе системы при этом почти равна нулю. Если z = /2, то амплитудно-частотная характеристика имеет пик на частоте затухающих колебаний (см. рис.2.45 (а) и (b)).

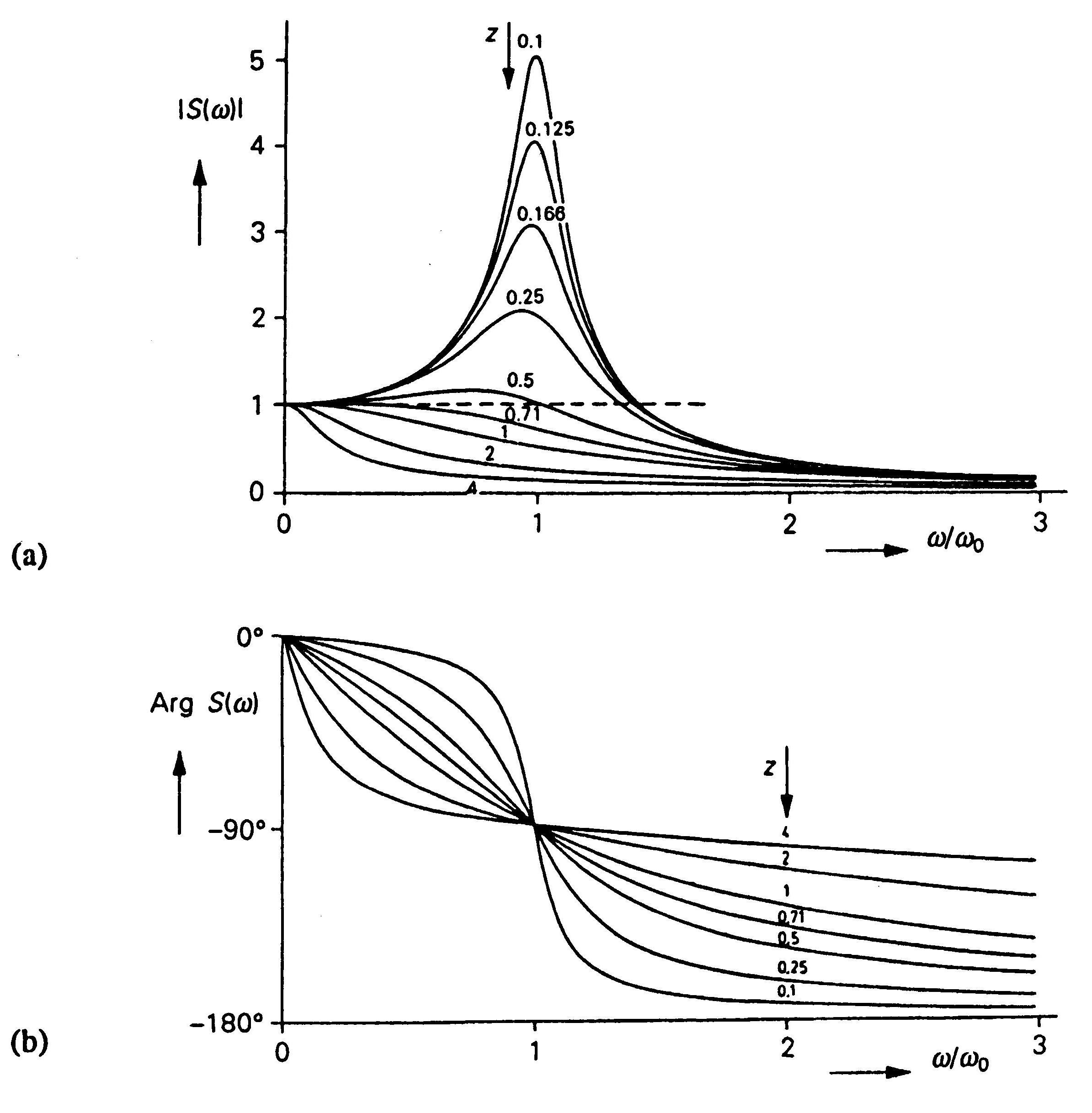
Рис. 2.45. (а) Амплитудно-частотная и (b) фазо-частотная характеристики си­стемы второго порядка при различных значениях коэффициента затухания z.