Тема 2: «Табличный процессор ms Excel. Работа с массивами».

Решить систему линейных уравнений:

Решение данного уравнения произведём методом обратной матрицы.

С помощью обратной матрицы решаются системы n линейных уравнений с n неизвестными, определитель которых отличен от 0 (нуля).

Для этого систему линейных уравнений , где запишем в виде матричного уравнения: , где – квадратная матрица, составленная из коэффициентов неизвестных.

Решение матричного уравнения имеет вид .

Решение:

1. представим систему уравнений в виде матричного уравнения:

;

2. левая часть этого уравнения в виде матрицы А записывается в виде массива $A$4:$D$7 (рис. 23);

3. в расчетах применяются аргументы функции МОБР и МУМНОЖ;

4. Для ускорения процессов расчета матриц используется комбинация клавиш Ctrl+Shift+Enter.

Рис. 23. Исходная матрица А

Для вычисления обратной матрицы на пустом месте выделяем такую же квадратную матрицу: это пустой массив $F$4:$I$7.

Курсором выделяем ячейки массива $F$4:$I$7.

Выбираем функцию МОБР и в окно Массив вводим массив $A$4:$D$7 (см. рис. 24) и набираем комбинацию клавиш Ctrl+Shift+Enter.

Рис. 24. Ввод массива данных для вычисления обратной матрицы

На рис. 25 показаны уравнения, введенные в соответствующие ячейки, а на рис. 26 – вычисленная обратная матрица .

Рис. 25. Уравнения, введенные в ячейки для вычисления МОБР

Рис. 26. Обратная матрица

Вычисление переменных производится с на основании решения матричного уравнения вида .

На пустом месте выделяем массив $K$4:$K$7.

В ячейки $K$4:$K$7 вводятся значение переменных .

Курсором выделяем ячейки массива $N$4:$N$7.

Выбираем функцию МУМНОЖ и в окно Массив 1 вводим массив $F$4:$I$7 – это массив обратной матрицы, а в окно Массив 2 вводим массив $К$4:$К$7 (рис. 27) и набираем комбинацию клавиш Ctrl+Shift+Enter.

Рис. 27. Ввод массива данных для вычисления переменных

На рис. 28 показаны уравнения, введенные в соответствующие ячейки, а на рис. 29 – рассчитанные значения переменных .

Рис. 28. Уравнения, введенные в ячейки для вычисления МУМНОЖ

Рис. 29. Рассчитанные значения переменных

Результаты расчётов:

Проверим результаты расчётов путем решения уравнения .

Подставим в уравнение переменные , введём уравнение в ячейку H10 . В результате имеем . В ячейке H10 получили правильный результат.

Тема 3: «Табличный процессор ms Excel. Анализ данных».

При выполнении данного задания таблицу развернуть по вертикали и отсортировать по месяцам. Графики прогнозов строить отдельно. Сделать соответствующие выводы относительно прогнозной стоимости товаров.

Известна величина дохода ($), полученная от реализации одного изделия за последние 7 месяцев (рис. 30):

Рис. 30. Исходная таблица данных

Построить графики изменения стоимости каждого вида продукции и спрогнозировать их стоимости на 9-й месяц.

Этапы расчётов.

1. Чтобы развернуть таблицу по вертикали и отсортировать по месяцам, вначале необходимо выделить всю таблицу.

2. Скопировать таблицу в буфер.

3. Курсор устанавливаем в любую пустую ячейку.

4. В меню Правка выделить команду Специальная вставка (рис. 31). Подобные действия могут быть выполнены нажатием левой кнопкой мыши.

Рис. 31. Команда Специальная вставка в контекстном меню

5. Нажимаем левую кнопку мыши, вызываем диалоговое окно Специальная вставка (рис. 32). В диалоговом окне Специальная вставка выделяем команду транспонировать (рис. 32) и ОК.

Рис. 32. Диалоговое окно Специальная вставка

6. В выделенной ячейке появляется вертикальная матрица (рис. 33). Теперь её необходимо отсортировать по месяцам.

Рис. 33. Транспонированная вертикальная матрица

7. Курсор устанавливаем в ячейке В8 и в строке меню выбираем команду .

8. Получаем таблицу, в которой результаты расположены по вертикали и отсортированы по месяцам (рис. 34).

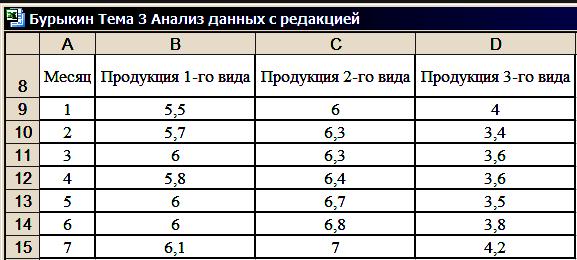
Рис. 34. Результаты в таблице отсортированы по вертикали

9. Дальнейшие действия связаны с построением графиков прогноза по каждому виду продукции. Используется подбор кривой по точкам.

Выполняются следующие действия:

1. Мастер диаграмм  Точечная (рис. 35). Выполняем 4 шага Мастера диаграмм (рис. 36-38).

Рис. 35. Мастер диаграмм: (шаг 1 из 4): вид диаграммы Точечная

Рис. 36. Мастер диаграмм: (шаг 2 из 4): источник данных диаграммы

Рис. 37. Мастер диаграмм: (шаг 3 из 4): параметры диаграммы

2. Разместить на отдельном листе Готово (рис. 33).

Рис. 38. Мастер диаграмм: (шаг 1 из 4): размещение диаграммы

3. На диаграмме щелкнуть на любой точке ряда данных (выделится весь ряд данных). В меню Диаграмма выбираем команду Добавить линию тренда. В расчетах выбрана Степенная линия тренда (рис. 39).

Рис. 39. Выбор степенной линии тренда

3. В меню Параметры выбираем команду Прогноз вперёд на: 2 единиц, и команды: показать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации ( ) – это коэффициент детерминации (рис. 40). Нажимаем ОК и получаем график (рис. 41).

Рис. 40. Выбор периодов прогноза, вида уравнения и коэффициента

Рис. 41. Прогноз стоимости продукции 1-го вида

Уравнение степенной линии тренда имеет вид:

.

Коэффициент детерминации имеет довольно высокое значение и показывает, что в расчётах учтены 84,38% значимых факторов. На долю неучтенных факторов приходится 15,62%. Это свидетельствует о высокой точности расчётов.

Результаты расчётов прогноза стоимости продукции 1-го вида.

1. Прогноз на два периода планирования вперёд показал, что на 8-м периоде стоимость продукции 1-го вида увеличится до величины 6,12.

2. На 9-м периоде стоимость продукции 1-го вида увеличится до величины 6,16.

3. В целом вид кривой характеризует о тенденции постепенного роста стоимости продукции 1-го вида.

Прогноз стоимости продукции 2-го и 3-го вида производится аналогично, поэтому по каждому виду продукции 2-го и 3-го вида приведём графики прогнозов и соответствующие выводы относительно прогнозной стоимости товара каждого вида.

Прогноз стоимости продукции 2-го вида на основании степенной линии тренда показан на рис. 42.

Рис. 42. Прогноз стоимости продукции 2-го вида

Уравнение степенной линии тренда имеет вид:

.

Коэффициент детерминации имеет довольно высокое значение и показывает, что в расчётах учтены 90,27% значимых факторов. На долю неучтенных факторов приходится 9,73%. Это свидетельствует о высокой точности расчётов.

Результаты расчётов прогноза стоимости продукции 2-го вида.

1. Прогноз на два периода планирования вперёд показал, что на 8-м периоде стоимость продукции 2-го вида увеличится до величины 6,86.

2. На 9-м периоде стоимость продукции 2-го вида увеличится до величины 6,95.

4. В целом вид кривой характеризует о тенденции постепенного роста стоимости продукции 2-го вида.

Рассмотрим прогноз стоимости продукции 3-го вида.

Предварительные расчёты показали, что все рассчитанные коэффициенты детерминации, кроме полиномиальной линии тренда имеют очень низкое значение:

• линейная линия тренда ;

• логарифмическая линия тренда ;

• экспоненциальная линия тренда ;

• степенная линия тренда .

В расчётах для прогноза стоимости 3-го вида продукции принята полиномиальная линия тренда.

Прогноз стоимости продукции 3-го вида показан на рис. 43.

Рис. 43. Прогноз стоимости продукции 3-го вида

Уравнение полиномиальной линии тренда имеет вид:

.

Коэффициент детерминации имеет высокое значение и показывает, что в расчётах учтены 79,87% значимых факторов. На долю неучтенных факторов приходится 20,13%. Это свидетельствует о достаточной точности расчётов.

Результаты расчётов прогноза стоимости продукции 3-го вида.

3. Прогноз на два периода планирования вперёд показал, что на 8-м периоде стоимость продукции 3-го вида увеличится до величины 4,64.

4. На 9-м периоде стоимость продукции 3-го вида увеличится до величины 5,24.

5. В целом вид кривой характеризует о тенденции постепенного роста стоимости продукции 3-го вида.