8

ЛАБОРАТОРНАЯ РАБОТА № 4

Сферический параллактический треугольник восход и заход светил

ЦЕЛЬ РАБОТЫ: Ознакомление с основными формулами сферического и параллактического треугольников. Решение задач на преобразование астрономических координат. Решение задач на определение места (А) и времени (s) восхода и захода светил.

НЕОБХОДИМОЕ ОБОРУДОВАНИЕ:

1. Таблицы тригонометрических функций.

2. Электронная клавишная вычислительная машинка (ЭКВМ) или персональный компьютер (ПК).

3. Задание (получить у преподавателя).

ВОПРОСЫ К ДОПУСКУ:

1. Сферический треугольник.

2. Основные формулы сферического треугольника: формулы синусов, косинусов, пяти элементов.

3. Параллактический треугольник, его углы и стороны.

4. Формулы перехода от горизонтальной системы астрономических координат к экваториальным координатам и обратно.

5. Формулы для нахождения азимута А и времени s восхода и захода светил.

ЛИТЕРАТУРА:

1. Кононович Э.В., Мороз В.И. Общий курс астрономии: Учебное пособие. -М.: Едиториал УРСС, 2001, Гл.1, §§ 1.20-1.21, с.45-49.

2. Дагаев М.М. Лабораторный практикум по курсу общей астрономии. -М.: Высшая школа, 1972, с.81-93.

Методические указания к выполнению работы

I. Краткий теоретический материал

1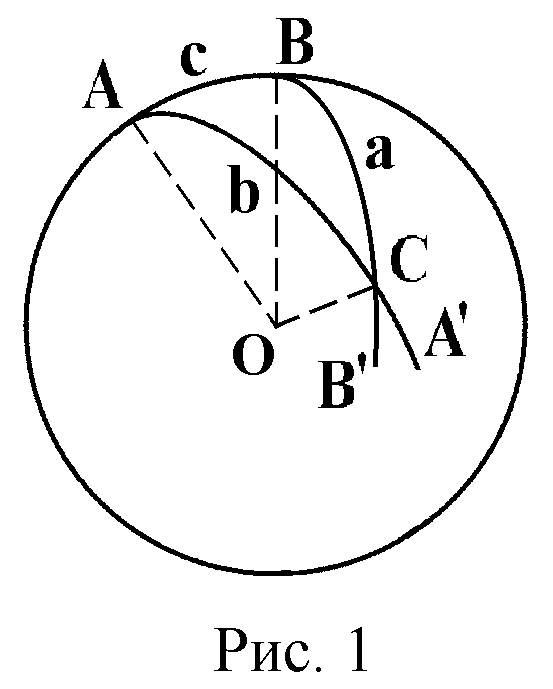 . Для решения многих астрономических задач, таких, в частности, как переход от одной системы астрономических координат к другой системе астрономических координат, определение времени и азимута восхода и захода светил и т.п., рассматривается сферический треугольник и применяются его основные формулы.

Сферическим треугольником называется фигура на сфере, образованная дугами трех больших кругов.

Пусть точка O – центр сферы (рис. 1). AB, AA' и BB' – дуги больших кругов. ABC – сферический треугольник. Углы треугольника: сф. угол BAC = A, сф. угол ABC = B, сф. угол ACB = C. Стороны сферического треугольника: BC = a, AC = b, AB = c (мера угловая). OABC – трехгранный угол.

2. Основные формулы сферического треугольника.

а) Формула косинусов.

Пусть в сферическом треугольнике ABC известны стороны b и c и угол A, образованный этими сторонами. Искомое значение стороны a получим через известные элементы треугольника:

cosa = cosbcosc + sinbsinccosA. (1)

Формула (1) – формула косинусов. Аналогично записываются формулы для косинусов сторон b и c:

б) Формула синусов.

Стороны и углы сферического треугольника связаны соотношением: отношение синуса угла к синусу противоположной стороны есть величина постоянная для всех углов и сторон сферического треугольника.

sinA/sina = sinB/sinb = sinC/sinc = M. (2)

Здесь M – модуль сферического треугольника. Формула (2) –формула синусов.

Формулу синусов можно (и удобно) записать в следующем виде:

sinAsinb = sinBsina,

sinAsinc = sinCsina, (2)

sinBsinc = sinCsinb.

в) Формула пяти элементов.

Пусть в сферическом треугольнике (рис. 1) известны две стороны и угол, образованный этими сторонами. Тогда

sinacosB = cosbsinc - sinbcosccosA. (3)

Выражение (3) – формула пяти элементов. Аналогичные соотношения можно записать для всех других комбинаций стороны и угла сферического треугольника.

Формулы косинусов, синусов и пяти элементов являются основными в сферической астрономии и будут использованы нами далее при решении задач преобразования координат и определения азимутов A и времени s восходов и заходов светил.

3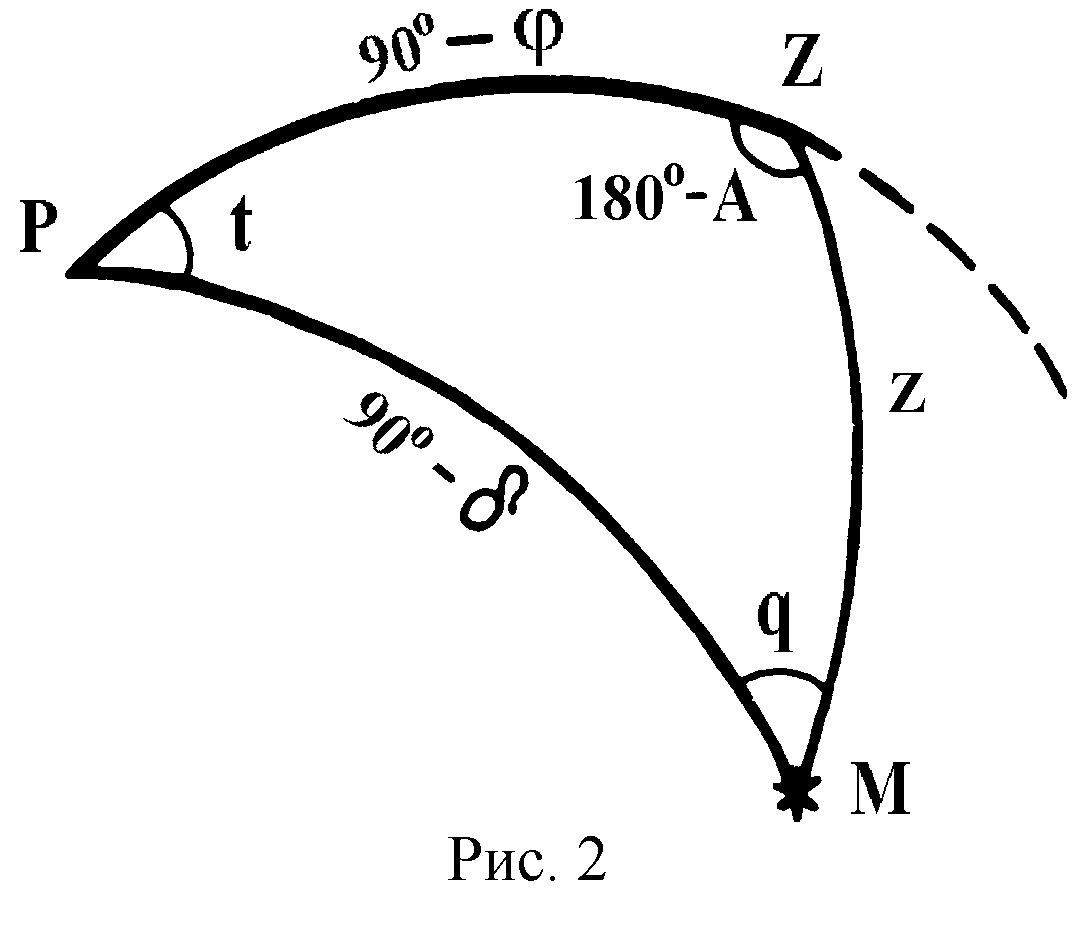 . На рис. 2: O – центр небесной сферы, M – светило, P – северный полюс мира, Z – зенит, PM = 90 -  – полярное расстояние светила M, ZM = z – зенитное расстояние светила M, ZP = 90 -  – зенитное расстояние северного полюса мира. Сферический треугольник ZMP – параллактический треугольник. В этом треугольнике:  – географическая широта места наблюдения,  – склонение светила М, сф. угол PZM =180 - A, где A – азимут светила М, сф. угол ZPM = t – часовой угол светила М, сф. угол ZMP= q – параллактический угол.

Рассматриваемый сферический треугольник является одним из вариантов параллактического треугольника. Поскольку параллактический треугольник есть треугольник сферический, для него справедливы все формулы сферического треугольника. Вид параллактического треугольника при наблюдении одного и того же светила зависит от момента наблюдения s и географической широты места наблюдения .

4. Формулы перехода от горизонтальной системы астрономических координат к экваториальным системам астрономических координат.

В параллактическом треугольнике ZMP (рис.2) известны: широта места наблюдения , азимут А светила М, высота h светила М (следовательно, известно и зенитное расстояние z, так как z = 90 - h). Известно и звездное время s момента наблюдения светила М. Из треугольника следует найти: склонение  и часовой угол t светила М.

Применим к стороне PM формулу косинусов (1):

cos(90 - ) = cos(90 - )cosz + sin(90 - )sinzcos (180 - A),

или

sin  = sincosz - cossinzcosA. (4)

Применим к стороне PM и углу ZPM формулу синусов (2):

sin(90 - )sint = sinzsin(180 - A),

или

cossint = sinzsinA (5)

Применим к стороне PM и углу ZPM формулу пяти элементов (3):

sin(90 - )cost = sin(90 - )cosz - cos(90 - )sinzcos(180 - A),

или

coscost = coscosz + sinsinzcos A. (6)

Разделим соотношение (5) на соотношение (6):

tgt = sinzsinA/(coscosz + sinsin zcosA). (7)

Значение часового угла t определяется значением азимута A: если значение А лежит в пределах <0  180>, то значение t находится в пределах <0^h  12^h>; если значение А лежит в пределах <180  360>, то значение t находится в пределах <12^h  24^h>.

Связь между часовым углом t светила, прямым восхождением этого светила и моментом наблюдения s по звездному времени выражается соотношением

 = s - t. (8)

Формулы (4), (7) и (8) – основные формулы перехода от горизонтальной системы астрономических координат (h и A) к первой и второй экваториальным системам координат (t,  и ).

5. Формулы перехода от экваториальных систем астрономических координат к горизонтальной системе координат.

В параллактическом треугольнике ZMP известны: широта места наблюдения , склонение  и прямое восхождение  светила М, звездное время s момента наблюдения светила М. Из треугольника следует найти зенитное расстояние z и азимут А светила М.

Применим к стороне ZM формулу косинусов (1):

cosz = cos(90 - )cos(90 - ) + sin(90 - )sin(90 - )cost,

или

cosz = sinsin + coscoscost. (9)

h = 90 - z.

Часовой угол t можно получить, используя формулу (8):

Применим к стороне ZM формулу синусов (2):

sinzsin(180 - A) = sin(90 - )sint,

или

sinzsinA = cossint. (10)

Применим к стороне ZM и углу PZM формулу пяти элементов (3):

sinzcos(180 - A) = sin(90 - )cos(90 -) - cos(90 - )sin(90 - )cost,

или

sinzcosA = - cossin + sincoscost. (11)

Разделим соотношение (10) на соотношение (11):

tgA = cossint/(-cossin + sincoscost). (12)

Значение азимута A определяется значением часового угла t: если значение t находится в пределах <0^h  12^h>, то значение А лежит в пределах <0  180>; если значение t находится в пределах <12^h  24^h>, то значение А лежит в пределах <180  360>.

Формулы (9) и (12) – основные формулы перехода от экваториальных систем астрономических координат (t,  и ) к горизонтальной системе астрономических координат (h и A).

6. Определение места и времени восхода и захода светил.

П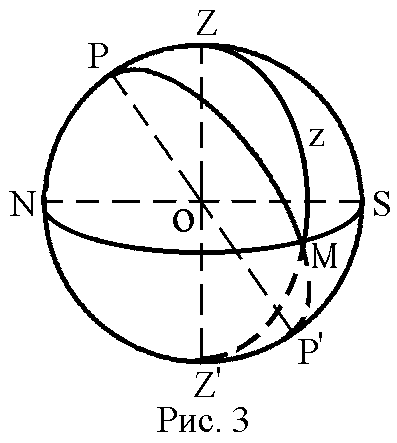 усть на какой-либо широте  в момент наблюдения s светило M находится на истинном горизонте, то есть наблюдается либо истинный восход, либо истинный заход этого светила (рис. 3). Будем считать светило точечным объектом и пренебрежем рефракцией и понижением видимого горизонта. Тогда z = 90 и параллактический треугольник ZPM – прямосторонний: cosz = 0, sinz = 1. Из (4):

sin = - coscosA,

cosA = - sin/cos. (13)

Формула (13) дает два значения азимута A: A_зах = A – азимут точки захода, A_восх = 360 - A – азимут точки восхода.

Так как светило M находится на истинном горизонте, то из (9):

cost = - sinsin /coscos

cost = - tgtg. (14)

Формула (14) дает два значения часового угла t: t_зах = t – часовой угол точки захода, t_восх = 24^h - t – часовой угол точки восхода.

Для моментов восхода и захода по звездному времени получаем:

s_зах =  + t_зах, s_восх =  + t_восх. (15)

7. При определении часовых углов и азимутов восхода и захода Солнца и Луны следует учитывать экваториальные горизонтальные параллаксы этих светил (p_⊙  8,8 и p_  57), их угловые радиусы (_⊙  16 и _  16) и значение атмосферной рефракции  при z = 90 (_90° = 35).

Из соотношения (9) получаем формулу для вычисления часового угла t:

cost = [cos(90 + _90 - p + ) - sinsin]/coscos. (16)

Из соотношения (4) получаем формулу для вычисления азимута A:

cosA = [-sin+ cos(90 + _90 - p + )sin]/cossin(90 +

+ _90 - p + ). (17)