1.6. Закон джоуля – ленца

Если ток в цепи постоянен, а проводники, входящие в цепь, неподвижны, работа сторонних сил полностью расходуется на нагревание проводников. Тепловую энергию обозначим W.

Объемной плотностью тепловой мощности тока называется энергия, выделяющаяся в единице объема проводника за единицу времени. Закон Джоуля -Ленца в дифференцированной форме имеет вид:

– объемная плотность тепловой мощности тока равна скалярному произведению векторов плотности тока и напряженности электрического поля.

Объемная плотность тепловой мощности тока прямо пропорциональна квадрату напряженности электрического поля, создающего ток, и удельной проводимости проводника.

Интегрируя это выражение по объему проводника, получим закон Джоуля – Ленца в интегральной форме: количество теплоты, выделяемой в проводнике, пропорционально силе тока, времени его прохождения и падению напряжения:

.

Классическая электронная теория дает следующее объяснение рассматриваемому выше закону. Кинетическая энергия электрона в конце пробега

.

При столкновении с ионом кристаллической решетки электрон отдает свою энергию, поэтому внутренняя энергия металла возрастает (металл нагревается), число соударений одного электрона , поэтому в единицу времени в единице объема выделяется тепло:

.

Для энергии dW имеем: , причем объем .

Проинтегрировав это выражение, получаем: , причем , , тогда .

Таким образом, количество теплоты, выделяемой в проводнике, равно

.

Рассмотрим электрическую цепь, состоящую из источника тока с ЭДС и внутренним сопротивлением r и нагрузки сопротивлением R (рисунок 7).

Рисунок 7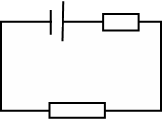

По закону Ома ток в цепи равен:

.

Напряжения на нагрузке U совпадает с напряжением на зажимах источника и равно:

.

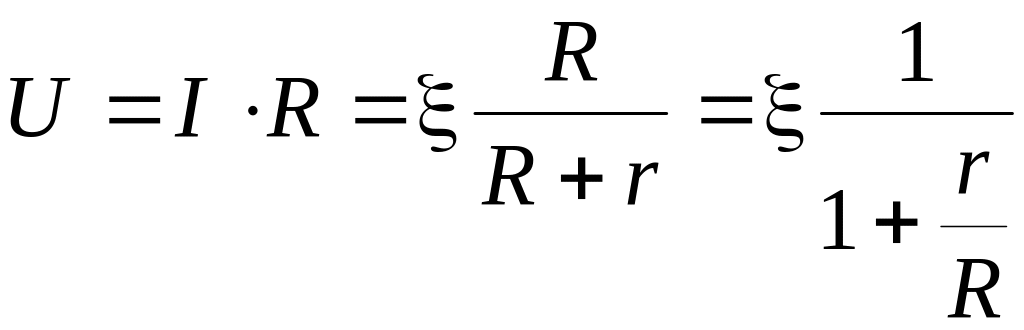Напряжение U всегда меньше , если цепь разомкнута, R→∞ и U =  .

Полная мощность, развиваемая в цепи источником тока равна

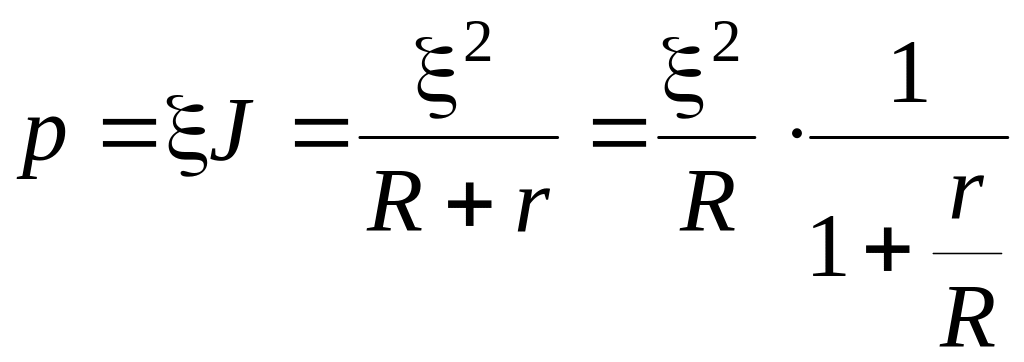. (4)

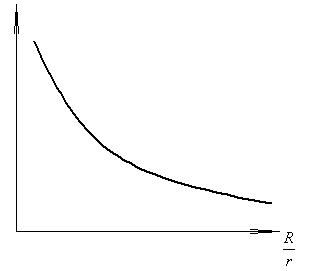
Зависимость полной мощности по отношению представлена на рисунок 8.

Рисунок 8.

На нагрузке выделяется не вся мощность р, а часть её, называемая полезной:

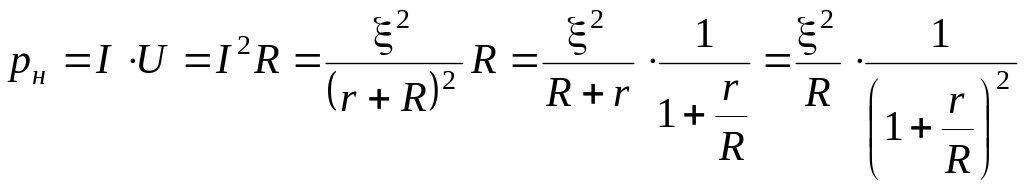. (5)

Полезная мощность имеет максимальные значения, когда производная функции по переменной R равна нулю: . Это имеет место при R = r.

Рисунок 9.

Зависимость полезной мощности от отношения представлена на рисунке 9.

КПД будет тем больше, чем меньше отношение , т.е. чем больше сопротивление нагрузки R. При размыкании цепи R→∞ и η = 1. Однако при этом мощность, выделяемая во внешней цепи, стремиться к нулю, поэтому условие максимума КПД с практической точки зрения не интересно. Наиболее притягательная область R~r₀ , в которой полезная мощность наибольшая и η~0,5.

2.Описание установки и методики измерений

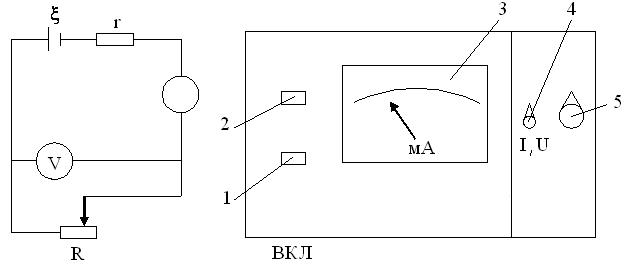
Для исследования мощности используется лабораторная установка (рисунок 10), выполненная в виде прибора настольного типа и содержащая смонтированные в одном корпусе специализированный источник питания, который по своим характеристикам является аналогом аккумулятора; стрелочный вольтмиллиамперметр с пределами измерений напряжения от 0 до 25В; нагрузка-реостат с сопротивлением несколько сот Ом. Питание установки осуществляется от сети напряжением 220 В. На лицевой панели прибора (рисунок 10) расположены клавиша 1 включения источника питания «ВКЛ», под которой помещена сигнальная лампочка 2, шкала вольтмиллиамперметра 3, переключатель 4 измерений I/U, ручки потенциометра 5. В положении «I» переключателя 4 стрелочный прибор показывает силу тока, в положении «U» - напряжение на нагрузке. Потенциометр R меняет сопротивление нагрузки от нуля до максимального значения.

Схема установки представлена на рисунок 10.

Рисунок 10.

Установка включается в сеть напряжением 220В.

В работе предусматривается определение внутреннего сопротивления r и ЭДС источника двумя способами – графическим и расчетным.

Графический метод определения внутреннего сопротивления и ЭДС источника состоит в следующем. Меняя сопротивление реостата R потенциометром, фиксируют соответствующие значения тока J и напряжения на нагрузке. По формуле

p_Н = IU (6)

вычисляют полезную мощность, а по формуле

(7)

сопротивление нагрузки, и строят зависимость p_Н(R) . По графику определяют сопротивление R, при котором p_Н достигает максимума. В этом случае R = r.

По закону Ома

(8)

– по этой формуле вычисляют ЭДС источника.

Зная R и r, строят зависимости , , . При этом должно выполняться соотношение (1) = 0,5.

Более точный метод определения r и основан на применении метода наименьших квадратов (МНК) и включает в себя обработку результатов эксперимента на ЭВМ (см. Приложение 1). По данным эксперимента строят зависимость и апроксимируют ее прямой, уравнение которой имеет вид:

.

Напряжение U откладывают по оси ординат, ток I – по оси абсцисс. Точка пересечения этой прямой с осью ординат соответствует значению , тангенс угла наклона к оси абсцисс – сопротивлению r.