
- •Утверждено
- •Рыбинск 2009 правила техники безопасности
- •Приборы и оборудование: Источник питания, амперметр, вольтметр (смонтированы в одном корпусе), реостат.
- •1. Теоретические сведения
- •1. 1.Электрический ток. Сила и плотность тока
- •1.2. Электродвижущая сила
- •1.3. Закон ома. Сопротивление
- •1.4. Закон ома для неоднородного участка цепи
- •1.5. Мощность тока
- •1.6. Закон джоуля – ленца
- •2.Описание установки и методики измерений
- •3. Порядок выполнения работы
- •4. Обработка результатов
- •5. Обработка результатов эксперимента на эвм
- •6. Содержание отчета
- •7. Контрольные вопросы
- •8. Список литературы
- •Применение метода наименьших квадратов
- •Применение метода наименьших квадратов для
1.4. Закон ома для неоднородного участка цепи
На
носители тока на неоднородном участке
цепи действуют, кроме электростатических
сил
![]() ,
еще и сторонние силы
,
еще и сторонние силы
![]() .
Сторонние силы способны вызывать
упорядоченное движение носителей тока
так же, как и силы электростатические.
На неоднородном участке цепи средняя
скорость упорядоченного движения
носителей пропорциональна суммарной
силе
.
Сторонние силы способны вызывать
упорядоченное движение носителей тока
так же, как и силы электростатические.
На неоднородном участке цепи средняя
скорость упорядоченного движения
носителей пропорциональна суммарной
силе
![]() ,
тогда плотность тока
,
тогда плотность тока
![]() ,
(2)
,
(2)
это закон Ома для неоднородного участка цепи в дифференциальной форме.
Перейдем к интегральной форме этого закона. Рассмотрим неоднородный участок цепи. Допустим, что внутри этого участка существует линия (контур тока) удовлетворяющая следующим условиям:
в каждом сечении, перпендикулярном к контуру, величины ,
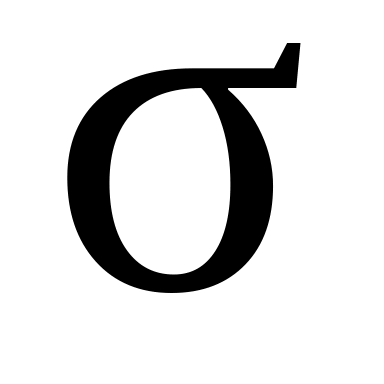 ,
,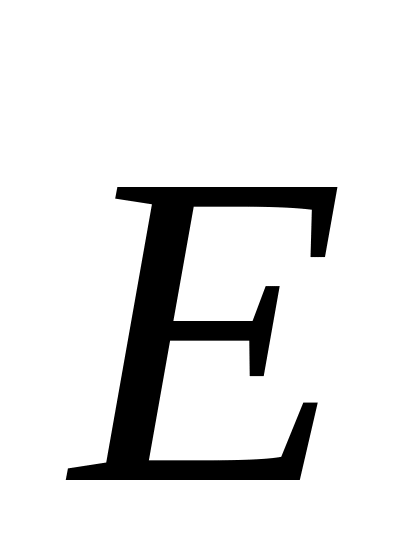 и
и
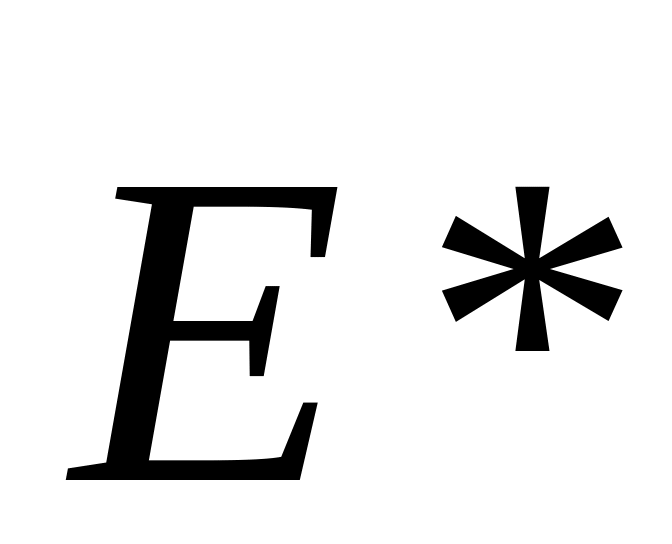 имеют с достаточной точностью одинаковые
значения;
имеют с достаточной точностью одинаковые
значения;векторы
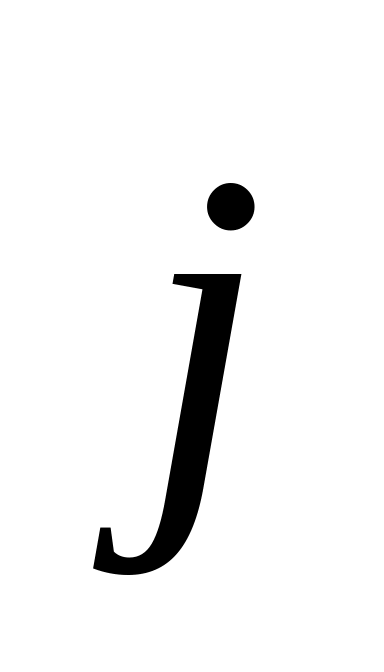 ,
,
,
, в каждой точке направлены по касательной
к контуру. Поперечное сечение проводника
может быть непостоянным.
в каждой точке направлены по касательной
к контуру. Поперечное сечение проводника
может быть непостоянным.
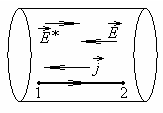
Рисунок
6.
![]() ,
(3)
,
(3)
причем
![]() ;
;
![]() ;
;
![]() .
Знак «+» берем в том случае, если ток
течет от 1 к 2, «-»если ток течет в
направлении 2 к 1. Вследствие сохранения
заряда сила постоянного тока в каждом
сечении должна быть одинаковой. Поэтому
вдоль контура
.
Знак «+» берем в том случае, если ток
течет от 1 к 2, «-»если ток течет в
направлении 2 к 1. Вследствие сохранения
заряда сила постоянного тока в каждом
сечении должна быть одинаковой. Поэтому
вдоль контура
![]() .
Силу тока в данном случае нужно
рассматривать как алгебраическую
величину. Направление 1-2 выбрано
произвольно, поэтому, если ток течет в
выбранном направлении, его считают
положительным, если в направлении 2-1 –
отрицательным. Заменим
.
Силу тока в данном случае нужно
рассматривать как алгебраическую
величину. Направление 1-2 выбрано
произвольно, поэтому, если ток течет в
выбранном направлении, его считают
положительным, если в направлении 2-1 –
отрицательным. Заменим
![]() ;
;
![]() ,
тогда из (3):
,
тогда из (3):
![]() .
.
Умножим
это выражение на
![]() и проинтегрируем вдоль контура:
и проинтегрируем вдоль контура:
![]() .
.
Здесь
![]() – сопротивление всей цепи,
– сопротивление всей цепи,
![]() – разность потенциалов на сопротивление
R,
– разность потенциалов на сопротивление
R,
![]() – ЭДС, действующая на участки 1,2. Тогда
– ЭДС, действующая на участки 1,2. Тогда
![]() ,
а ток
,
а ток
![]()
– это закон Ома для неоднородного участка цепи.
Если
цепь замкнутая, то
![]() ;
и
;
и
![]() .Тогда
.Тогда
![]() – закон Ома для замкнутой цепи. Если в
цепи действует несколько ЭДС, то
– закон Ома для замкнутой цепи. Если в
цепи действует несколько ЭДС, то
![]() равна их алгебраической сумме.
равна их алгебраической сумме.
1.5. Мощность тока
Рассмотрим
произвольный участок цепи постоянного
тока, к концам которого приложено
напряжение U.
За
время t
через каждое сечение проводника проходит
заряд
q = It,что
равносильно переносу заряда q
из одного конца проводника на другой.
При этом силы электростатического поля
и сторонние силы совершают работу
![]() ,
тогда мощность
,
тогда мощность
![]() .
.
Эта мощность может расходоваться на совершение работы участком цепи над внешними телами (для этого участок должен перемещаться в пространстве), на протекание химической реакции и на перемещение данного участка цепи.
Отношения мощности dp, развиваемой в объеме dV, к величине этого объема, называется удельной мощностью тока
![]() .
.
Найдем
выражение для удельной мощности тока.
Сила
![]() развивает при движении носителя тока
мощность:
развивает при движении носителя тока
мощность:
![]() ,
,
где
– скорость хаотического движения,
![]() – скорость упорядоченного движения
носителей.
– скорость упорядоченного движения
носителей.
Усредним
это выражение по носителям, заключенным
в объеме dV,
в пределах которого
и
![]() можно считать постоянными:
можно считать постоянными:
![]() .
.
Мощность
![]() ,
развиваемую в объеме
,
развиваемую в объеме
![]() ,
найдем, умножив
,
найдем, умножив
![]() на число носителей тока в этом объеме.
на число носителей тока в этом объеме.
![]() .
.
Подставив
![]() ,
имеем:
,
имеем:
![]()
