1.4. Hеpавновесное состояние полупpоводника

Неравновесное состояние полупроводника возникает при каком-либо внешнем энергетическом воздействии, в результате которого концентрации подвижных носителей заряда становяться отличными от равновесных. Таким воздействием может быть облучение полуроводника светом, в результате чего появляются дополнительные (избыточные) носители заряда. В полупроводниковых приборах неравновесное состояние полупроводника возникает обычно при введении в него (или выведении из него) неосновных носителей заряда из внешней електрической цепи через электронно-дырочный переход. Процесс введения неосновных носителей заряда называется инжекцией, а процесс выведения - экстракцией.

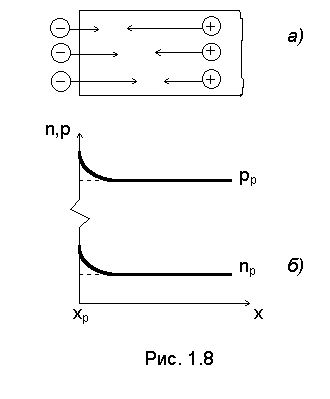
 Hа рис. 1.8,а представлен дырочный полупроводник, в который через сечение x_p инжектируются электроны. Пpи этом в полупpоводнике одновpеменно происходят два очень важных процесса. Во-пеpвых, возрастание концентpации электpонов на поверхности полупpоводника неизбежно ведет к возникновению их диффузии в глубинные области; диффундируя они встречаются с дырками и pекомбиниpуют. Во-втоpых, введение избыточных электpонов нарушает электpонейтpальность области, примыкающей к поверхности полупpоводника, что ведет к образованию внутреннего электрического поля, смещающего дырки из глубинных областей к поверхности полупpоводника, в pезультате чего происходит частичная компенсация инжектированного отрицательного заpяда. Вpемя, в течение котоpого происходит этот процесс, называется временем диэлектрической релаксации. Оно составляет около 10^-12с. Полной компенсации инжектированного заpяда произойти не может, так как в этом случае исчезнет внутреннее поле.

Таким образом в результате инжекции возрастает концентрация как неосновных, так и основных носителей заряда. На рис.1.8,б показано распределение концентрации электронов и дырок:

, (1.17)

. (1.18)

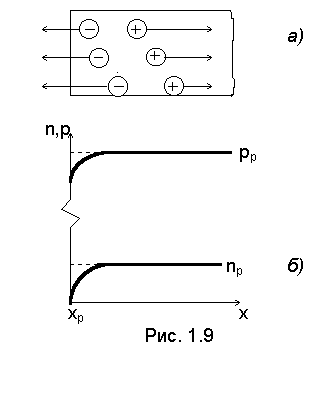
 Поскольку концентрации n_p и p_p отличаются на несколько порядков, то для совмещения графиков n(x) и p(x) средняя часть вертикальной оси удалена. При этом выполняется условие)  n(x)   p(x). В случае экстракции электронов из дырочного полупроводника (рис. 1.9,а) происходит уменьшение концентрации электронов в приповерхностной области и возникает диффузия электронов в направлении справа налево. При этом также возникает внутреннее электрическое поле, сдвигающее дырки вглубь полупроводника. Распределение концентрации электронов и дырок:

, (1.19)

. (1.20)

принимает вид, показанный на рис. 1.9,б.

Время жизни неосновных носителей заряда

Неравновесное состояние существует до тех пор пока не прекращается внешнее воздействие на полупроводник. После прекращения внешнего воздействия полупроводник возвращается в равновесное состояние. Длительность этого переходного процесса определяется временем жизни неравновесных носителей заряда. Поскольку концентрация основных носителей заряда при внешнем воздействии изменяется незначительно, то можно ограничиться только рассмотрением времени жизни неосновных носителей заряда. Для дырочного полупроводника после прекращения инжекции в него электронов изменение неравновесной концентрации электронов обусловлено разностью скоростей рекомбинации и генерации, то есть :

, (1.21)

где:

- скорость рекомбинации электронов, определяемая полной концентрацией: n(t) =n_p+ n(t); - скорость генерации электронов, определяемая равновесной концентрацией n_p.

Следовательно :

. (1.22)

Разделяя переменные и интегрируя в пределах от t₀ до t и от  n(t₀) до  n(t), получаем:

, (1.23)

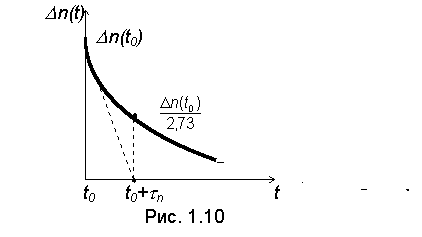
то есть избыточная концентрация с течением времени уменьшается по экспоненциальному закону (рис. 1.10). Время, в течение которого избыточная концентрация уменьшается в e раз ( e  2,7) называется временем жизни неравновесных носителей. В электронном полупроводнике аналогичным образом изменяется избыточная концентрация дырок.

Время жизни электронов является величиной, обратной вероятности встречи электрона с дыркой, которая равна  · p, где  - коэффициент рекомбинации, определяемый структурой кристаллической решетки полупроводника, а время жизни дырки - величина, обратная вероятности встречи с электроном. Вероятность такой встречи практически незначительна. В реальных структурах рекомбинация происходит по схеме “зона - ловушка - зона”.

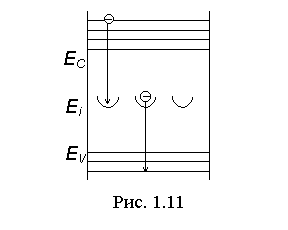
Ловушками называются разрешенные энергетические уровни, возникающие посередине запрещенной зоны за счет дефектов кристаллической структуры. При таком механизме рекомбинации электроны сначала захватываются ловушкой ( при этом рекомбинации дырки не происходит), а затем переходят в валентную зону (происходит рекомбинация дырки). (Рис. 1.11). В этом случае время жизни электронов является величиной , обратной вероятности захвата электрона ловушкой. При этом захват может быть осуществлен свободной ловушкой. Если M - концентрация ловушек, то M[1-P(E_i)] - концентрация свободных ловушек, где P(E_i) - вероятность нахождения электрона посередине запрещенной зоны, то есть в ловушке. Вероятность P(E_i) зависит то положения уровня Ферми. Следовательно:

, (1.24)

соответственно рекомбинация дырок происходит через занятые ловушки, следовательно:

. (1.25)

Уравнения (1.24) и (1.25 ) позволяют сделать вывод о причинах, влияющих на время жизни неравновесных носителей заряда.

Во-первых, время жизни зависит от концентрации ловушек M. Чем больше дефектов в кристаллической структуре полупроводника, тем меньше время жизни.

Во-вторых, время жизни зависит от концентрации примесей. Чем больше содержится примесей, тем дальше от середины запрещенной зоны расположен уровень Ферми. Поэтому в электронном полупроводнике возрастает P(E_i) и соответственно уменьшается  _p, а дырочном полупроводнике возрастает [1- P(E_i)] и соответственно уменьшается  _n.

В-третьих, время жизни зависит от температуры. С повышением температуры уровни Ферми в электронном и дырочном полупроводниках сдвигаются к середине запрещенной зоны. Кроме того, графики P(E) приобретают более плавный изгиб. Поэтому уменьшается P(E_i) в электронном полупроводнике и уменьшается [1-P(E_i)] в дырочном полупроводнике. В результате чего с ростом температуры возрастает время жизни неравновесных носителей заряда.

2.2. P-n-переход при подаче внешнего напряжения

Рассчитаем прямой и обратный токи p-n-перехода, исходя из основных процессов в базе диода. Будем по-прежнему считать, что концентрация донорной примеси в эмиттере N_D = n_n значительно превышает концентрацию акцепторной примеси в базе N_A = p_p. В этом случае и при прямом и при обратном напряжении можно учитывать только электронную  составляющую тока  i = i_n + i_p  i_n .

В самом деле, при прямом напряжении прямой ток определяется потоком основных носителей заряда, а т.к.  n_n  » p_p   , то дырочной составляющей прямого тока можно пренебречь. При обратном напряжении обратный ток определяется потоком неосновных носителей заряда;  поскольку

,

то и в этом случае дырочной составляющей обратного тока можно пренебречь.

Рассматривая процессы в p-n-переходе при подаче внешнего напряжения будем так же полагать, что сопротивление обедненной области, где подвижных носителей заряда практически нет, значительно больше, чем сопротивление областей n- и p-типа вне перехода. Это допущение позволит считать, что все внешнее напряжение падает на p-n-переходе и контактная разность потенциалов соответственно изменяется до величины  _K0±U, где знак “-” соответствует падению потенциального барьера вследствие подачи прямого напряжения на p-n-переход, а знак “+”  - при подаче обратного напряжения(см. рис.2.2,а).

Распределение потенциала вдоль структуры p-n-перехода показано на рис.2.2,б.

 

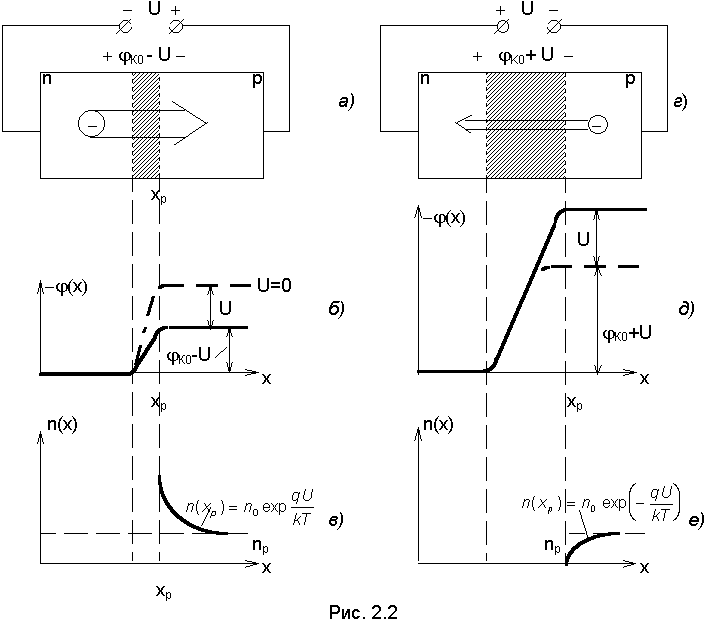
При прямом напряжении (U >0)  уменьшение потенциального барьера приводит к преобладанию потока электронов из  эмиттера в базу (ПОНЗ) над потоком электронов из базы в эмиттер (ПННЗ). При этом электроны инжектируются в базу и концентрация электронов на границе x_p возрастает до величины

,

которая уже при U=0,26 В  ( =0,026В)

значительно превышает равновесную концентрацию в базе. Таким образом, инжекция   электронов  в   базу   приводит  к   появлению  неравновесных  носителей  в базе n(x_p) = n (x_p) - n_p .  Вследствие возникшего градиента концентрации в базе начинается процесс диффузии электронов от границы перехода x_p в глубину p-базы. По мере движения неравновесная концентрация уменьшается за счет рекомбинации.

Таким образом, три процесса определяют распределение неравновесной концентрации в базе p-n-перехода при прямом напряжении:

- инжекция - вызывает увеличение граничной концентрации n(x_p), то есть приводит к появлению неравновесных носителей заряда в базе;

 - диффузия - является причиной движения электронов (ННЗ) через базу;

- рекомбинация - приводит к уменьшению неравновесной концентрации в базе вдали от p-n-перехода.

Распределение концентрации электронов в базе показано на рис. 2.2,в, оно описывается уравнением (1.34)

,

где - граничная концентрация  ,

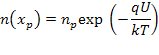
L_n -диффузионная длина электронов в базе.

Прямой электронный ток через p-n-переход может быть определен в любом сечении двухэлектродной структуры, однако удобнее это сделать в сечении x_p, где задана граничная концентрация .электронов

По своей природе электронный ток в сечении x_p является диффузионным и может быть рассчитан по формуле (1.44)

,

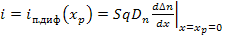где S - площадь p-n-перехода, q - заряд электрона, D_n - коэффициент диффузии электронов.

С учетом

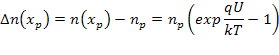
прямой ток p-n- перехода определяется выражением:

.      (2.5)

Обозначим , эта величина имеет размерность тока, определяется концентрацией неосновных носителей заряда в базе n_p и называется тепловым током i₀.

Проведя аналогичные рассуждения для обратного смещения, отметим следующее: p-n-переход при обратном смещении экстрагирует (выводит) электроны из базы. Граничная концентрация уменьшается по сравнению с равновесной и определяется выражением:  

,

которое отличается от соответствующего выражения при прямом напряжении полярностью напряжения U в экспоненте.

Три процесса определяют обратный ток p-n-перехода:

- экстракция электронов из базы;

- диффузия  их из глубины базы к границе перехода x_p;

- генерация  пар  электрон - дырка в областях, где n(x)<n_p.

Распределение потенциала (x) и концентрации n(x) для обратного напряжения приведены на рис. 2.2 г,д,е  - правый столбец.

Вывод выражения для электронной составляющей обратного тока через p-n-переход полностью аналогичен выводу прямого тока.

 Выражение для электронной составляющей обратного тока отличается от (2.5) только знаком внешнего напряжения и имеет вид :

.

Таким образом, ВАХ  p-n-перехода описывается выражением

,

где i₀ - тепловой ток p-n-перехода, с учетом дырочной составляющей тепловой ток может быть записан в виде:

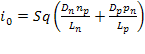 .      (2.6)

Тепловой ток p-n-перехода определяется потоками  ННЗ и зависит от концентрации примеси  ( так как n_p = n_i²/N_A; p_n = n_i²/N_D )  и температуры (так как:   n_i²~ exp T² ).

Увеличение температуры p-n- перехода приводит к увеличению теплового тока, а, следовательно,  к возрастанию прямого и обратного токов.

 Увеличение концентрации легирующей примеси приводит к уменьшению теплового тока, а, следовательно,  к уменьшению прямого и обратного токов p-n-перехода.

На рис. 2.3 построена ВАХ идеального p-n-перехода, полученного при принятых нами допущениях. При построении ВАХ  примем T= 300К, тогда kT/q = 0,026В. Оценим прямой и обратный токи p-n перехода при подаче внешнего напряжения U=±0,26 В. При         U=+0,26 В (прямое напряжение) (2.5) приводится к виду:

i = i₀• (exp 10 – 1)  i₀·exp 10 >> i₀

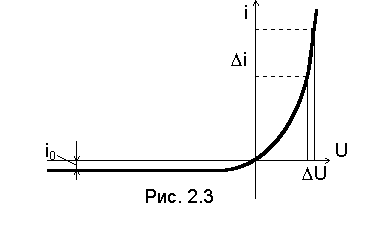
Таким образом, уже при U = 0,26 В величина прямого тока значительно превышает тепловой ток p-n перехода.

При U = - 0,26 В  (обратное напряжение)

i = i₀ · (exp–10 – 1)  - i₀.

Таким образом, при обратном напряжении через p-n переход протекает тепловой ток i₀ , значение которого не зависит от величины приложенного обратного напряжения.

ВАХ p-n-перехода представляет собой нелинейную зависимость между током и напряжением. В общем случае к p-n-переходу может быть приложено как постоянное напряжение, определяющее рабочую точку на характеристике, так и переменное напряжение, амплитуда которого определяет перемещение рабочей точки по характеристике. Если амплитуда переменного напряжения мала, перемещение рабочей точки не выходит за пределы малого участка характеристики и его можно заменить прямой линией. Тогда между малыми амплитудами тока и напряжения (или между малыми приращениями тока и напряжения i и u) существует линейная связь. В этом случае p-n-переход на переменном токе характеризуют дифференциальным сопротивлением r_pn:

.

Аналитическое выражение r_pn получим, дифференцируя (2.5)

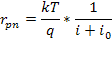
При прямом напряжении r_pn мало и составляет единицы - сотни ом, а при обратном напряжении - велико и составляет сотни и тысячи килоом.

Дифференциальное сопротивление можно определить графически по характеристике. (См. рис. 2.3, где указаны  u и i).