1.2.1. Расчетные соотношения для выпрямителей с активно- емкостной нагрузкой

Для получения удобных для применения на практике соотношений при анализе выпрямителей с активно-емкостной нагрузкой приняты следующие допущения и упрощения:

-диод будем считать идеальным (Е₀ = 0; I_обр = 0);

-конденсатор С имеет достаточно большую ёмкость, так что напряжение на нем постоянно и равно U₀;

-напряжение на вторичной обмотке трансформатора изменяется по закону косинуса:

.

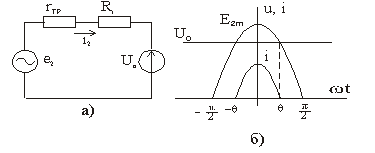
С учетом этого эквивалентная схема для проводящего состояния диода имеет вид, показанный на рис.1.7а (заряженный конденсатор по теореме компенсации заменен источником напряжения U₀).

График тока в цепи показан на рис.1.7б.

Согласно закону Ома:

.

Это выражение справедливо при , что имеет место при

, где .

Рис. 1.7.Схема замещения выпрямителя для проводящего состояния диода (а) и график тока диода (б)

Среднее значение тока диода для однополупериодной схемы является током нагрузки, для двухполупериодной – половиной тока нагрузки. Для получения общей формулы введём коэффициент р - число зарядных импульсов конденсатора С за период напряжения сети. Для однополупериодной схемы р = 1, для двухполупериодной р = 2.

.

Согласно рис.1.7б .

Обозначим - сопротивление, ограничивающее заряд конденсатора С. С учетом этих обозначений:

Выражение определяется через параметры выпрямителя и называется первым расчетным параметром выпрямителя А:

.

Так как уравнение не решается, то определение угла отсечки производится по графической зависимости .

Из выражения можно определить действующее значение напряжения на вторичной обмотке трансформатора Е₂ (в режиме холостого хода):

, где .

Для определения мощности силового трансформатора необходимо определить действующее значение тока вторичной обмотки трансформатора. Вначале определим действующее значение тока диода или действующее значение тока за половину периода:

.

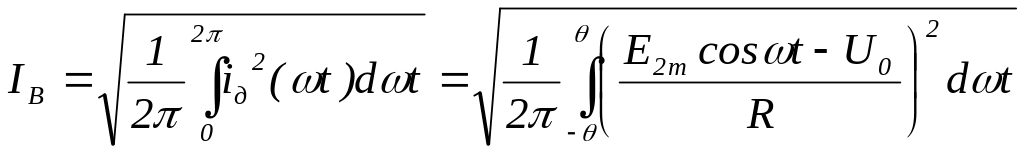После подстановок и и выполнения интегрирования получим:

, где D является функцией угла отсечки .

Для однополупериодной схемы и схемы со средней точкой ток вторичной обмотки трансформатора и ток диода совпадают по форме, поэтому для этих схем I₂ = I_В. Для мостовой схемы выпрямителя через вторичную обмотку протекают токи обеих пар диодов, поэтому:

.

Ток первичной обмотки трансформатора для однополупериодной схемы определяется с учетом того, что постоянная составляющая тока вторичной обмотки не трансформируется в первичную:

.

Для двухполупериодных схем ток первичной обмотки равен:

.

В выпрямителях с активно-емкостной нагрузкой ток диода имеет импульсный характер. Вследствие достаточно большой длительности импульса амплитудное значение тока диода не должно превышать допустимое прямое значение тока более чем в 4-5 раз. Поэтому в выпрямителях с активно-емкостной нагрузкой необходимо проверять выполнение этого условия.

,

и с учетом аналогичных подстановок получим:

,

где F является функцией угла отсечки .

В реальных условиях конденсатор С имеет конечную ёмкость, т.е. конкретное значение сопротивления конденсатора основной гармонике напряжения на конденсаторе. Падение напряжения на этом сопротивлении определяет пульсации выходного напряжения выпрямителя.

.

После подстановок и интегрирования получаем выражение:

.

Расчетный параметр Н является функцией не только угла отсечки , но и числа зарядных импульсов конденсатора р , и частоты сети .

Коэффициент пульсаций напряжения на нагрузке:

.

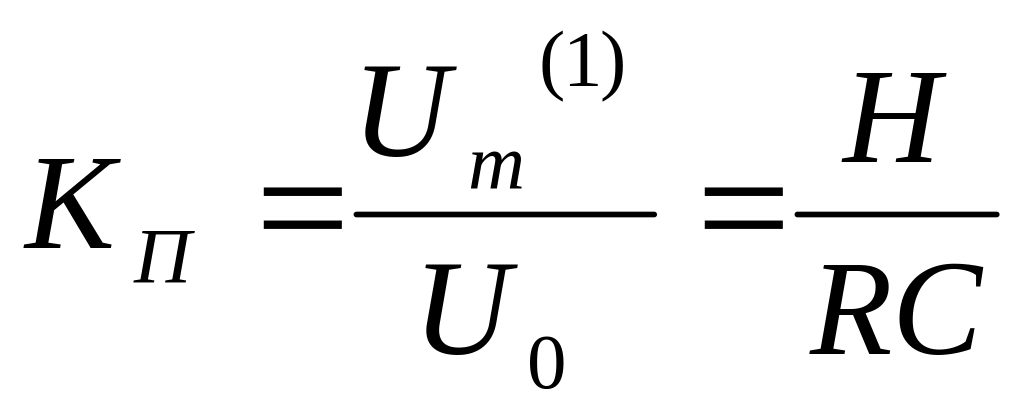Все полученные расчетные параметры A, B, D, F, H являются функциями угла отсечки , поэтому на практике приводятся зависимости параметров B, D, F, H от А: B(A), D(A), F(A), H(A;p;w) (рис.1.8).

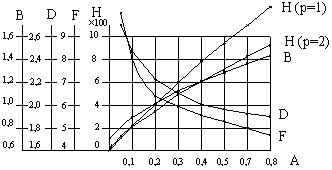
Рис. 1.8. Зависимости расчетных параметров выпрямителя от параметра А

0	30	38	45	50	54	57	60	62
A	0.05	0.1	0.2	0.3	0.4	0.5	0.6	0.7
B	0.82	0.91	1.03	1.12	1.21	1.28	1.36	1.43
D	2.7	2.46	2.22	2.1	2.02	1.97	1.93	1.9
F	10	8	6.4	5.9	5.6	5.3	5.0	4.7
H (1)	130	220	410	600	790	940	1100	1280
H (2)	125	210	350	490	600	710	820	920

Вследствие зависимости параметров выпрямленного напряжения от угла отсечки нагрузочная характеристика выпрямителя с активно-емкостной нагрузкой не является линейной. Общий вид нагрузочной характеристики определяется углом отсечки, поэтому целесообразно пользоваться нагрузочной характеристикой в координатах, являющихся функциями угла отсечки . Эти координаты получаются из ранее полученных соотношений для выпрямителя с активно-емкостной нагрузкой. Напряжение на нагрузке U₀ равно:

.

Ток нагрузки I0 равен:

или:

,

отсюда

.

Зависимость от выражения является обобщенной нагрузочной характеристикой (рис.1.9). Для получения реальной нагрузочной характеристики значение ординаты умножается на E_2m, а значение абсциссы умножается на сомножитель .