4.3Основной расчет тихоходного вала на прочность.

На практике установлено, что для валов основным видом разрушения яв­ляется усталостное, поэтому расчет на сопротивление усталости является ос­новным. Расчет выполним для сечения II. При совместном действии напряже­ний и изгиба запас сопротивления усталости определяют по формуле:

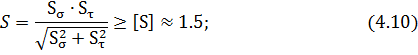
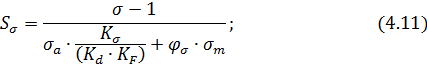
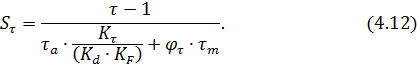
В этих формулах – амплитуды переменных составляющих циклов напряжения.

Путь напряжения изгиба, вращающегося вала, изменяются по симмет­ричному циклу (рисунок 4.2 а), а для напряжений кручения используем отнулевой цикл (рисунок 4.2 б).

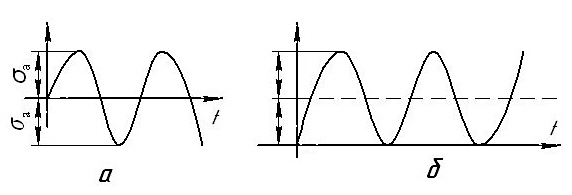
Рисунок 4.2

Согласно принятому условию:

где

– диаметр вала под зубчатое колесо

– диаметр вала под подшипник

Для нашего случая:

Значения – зависят, от механических характеристик материала и выбираются из таблицы 10.2 (ист. 1). Их значения принимаем: Пределы выносливости для нашего случая: . Эффективные коэффициенты концентрации напряжений выбираются по таблице 10.6 (ист. 1) и равны: .

Масштабный фактор и фак­тор шероховатости вырабатывают по графику (рисунок 4.3).

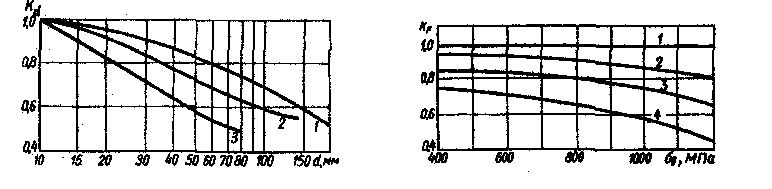
Рисунок 4.3

На рисунке 4.3 а, кривая 1 – относится к углеродистой стали, при отсутствии концентра­ции напряжений; 2 – легированная сталь при отсутствии концентрации напряжений и угле­родистая сталь при умеренной концентрации напряжений; 3 – легированная сталь при нали­чии концентрации напряжений. Для нашего случая следует использовать кривую 3. По гра­фику определяем

На рисунке 4.3 б, представлены четыре кривые: 1 – шлифование тонкое; 2 – обточка час­тая; 3 – обдирка; 4 – необработанная поверхность окалиной.

Для нашего случая следует принять тонкое шлифование. По графику определяем .

С учетом выбранных коэффициентов определяем:

Общий коэффициент запаса усталости определяется:

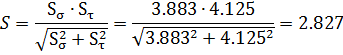
Результирующий коэффициент запаса прочности больше допустимого, что удовлетворяет условию прочности.

4.4 Расчет тихоходного вала на жесткость.

Упругие деформации вала отрицательно сказываются на работе связанных с ним деталей, подшипников, зубчатых колес, фрикционных передач и т.п. От прогиба вала в зубчатом зацеплении возникает концентрация напряжений по длине зуба. При больших углах поворота вала в подшипниках может произой­ти зацепление вала.

Перемещения при изгибе в общем случае целесообразно определять, ис­пользуя метод начальных параметров или интеграл Мора. В простых случаях можно использовать готовые решения. При этом вал рассматривают как имею­щий постоянное сечение некоторого приведенного диаметра. Определим, прогиб под силой используя формулу:

где F – радиальная сила. В нашем случае ;

a и b – расстояния между зубчатым колесом и подшипниками. В нашем случае a=0.092; b=0.025;

l – расстояние между подшипниками;

l=0.117;

E – модуль упругости первого рода. Находится по справочнику. ;

J – осевой момент инерции. Находится по формуле сопромата:

C учетом установленных параметров имеем:

Для зубчатых передач стрела прогиба под колесом - передачи ци­линдрические; - червячные. Для нашего случая мм. Делаем вывод. Вал удовлетворяет расчету на жесткость, сравнивая прогибы.