Вопрос 2. Математические модели индивидуального и коллективного риска. Биномиальная модель
В имущественном
страховании используется два основных
типа моделей: модель индивидуального
и коллективного
риска. В
модели индивидуального риска
рассматривается
полисов с независимыми выплатами
.
Ее характерными чертами являются
сравнительно короткий промежуток
времени для адекватного применения
модели, а также фиксированное и неслучайное
количество договоров
.
В модели коллективного риска по одному
полису допускается более одной выплаты,
количество подаваемых исков заранее
неизвестно, а рассматриваемая модель
носит динамический характер, когда
процесс подачи исков "растянут"
во времени.
Зададим некоторое
вероятностное пространство
и введем следующие понятия:
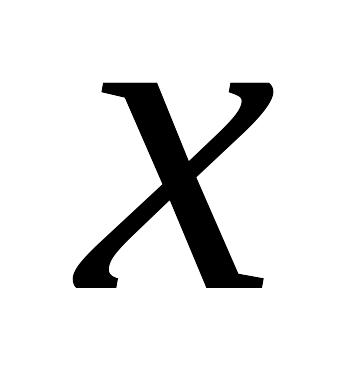– начальный
капитал
страховой компании.Неубывающая последовательность случайных величин
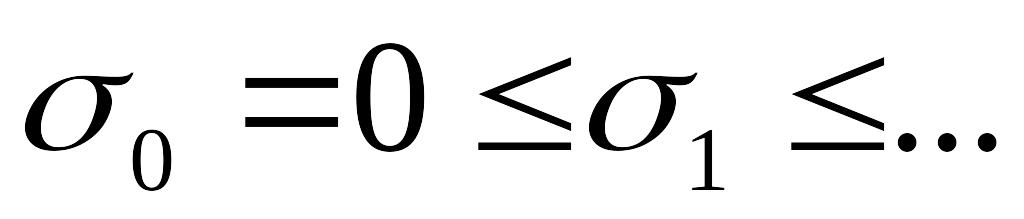– моменты наступления отдельных исков
от клиентов,
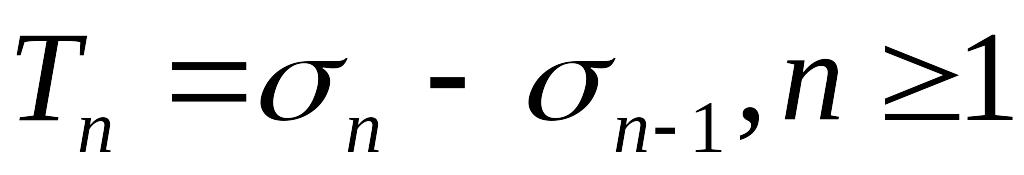– время между наступлениями исков.Общее количество поданных исков к моменту времени
:
,
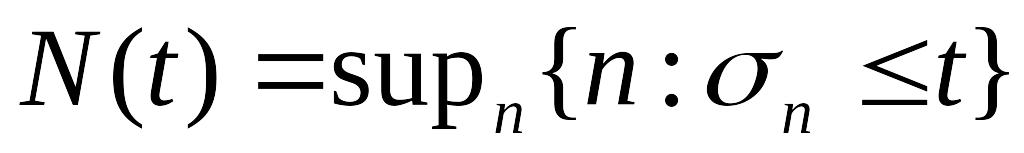при этом
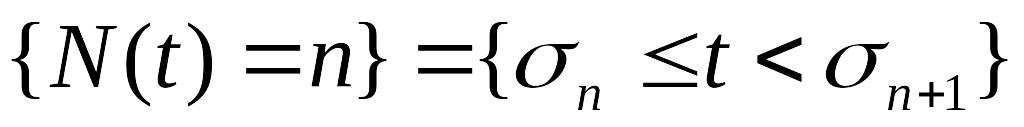.Последовательность независимых одинаково распределенных случайных величин
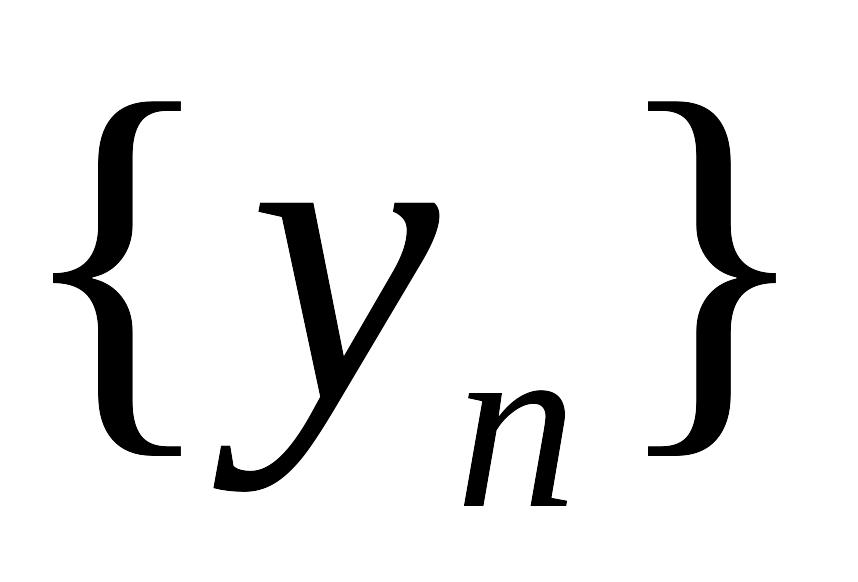определяет возможный размер исков
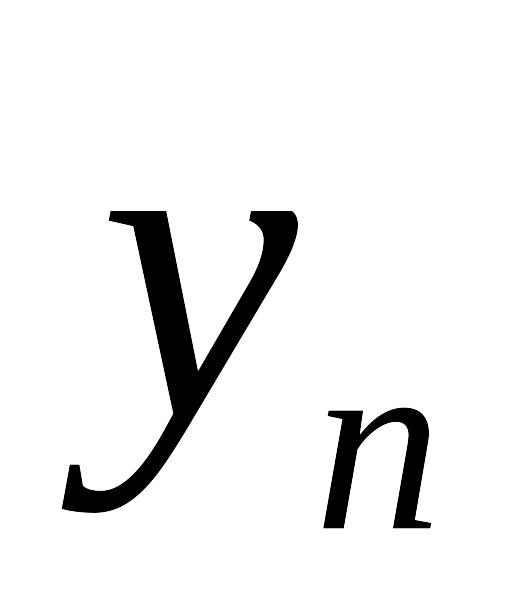в момент
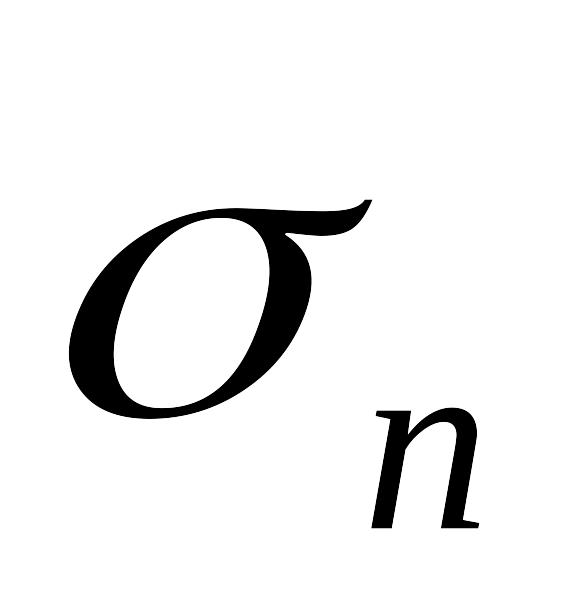с функцией распределения
,
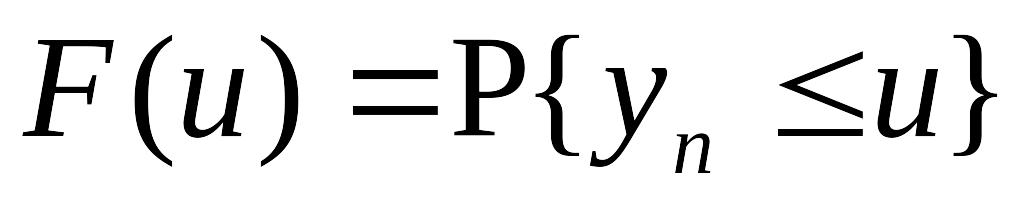.Процесс риска
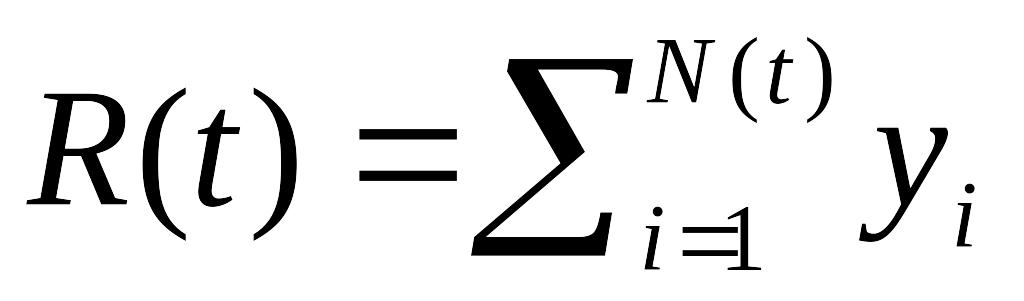определяет суммарные выплаты по искам
к моменту
,
,
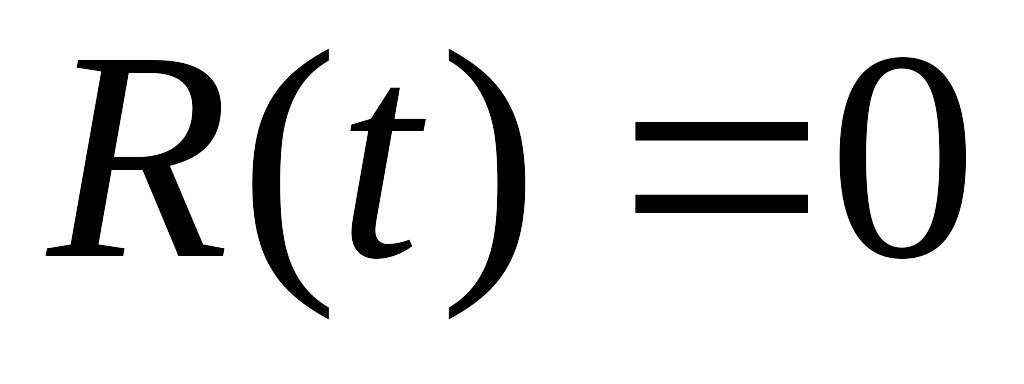если
.
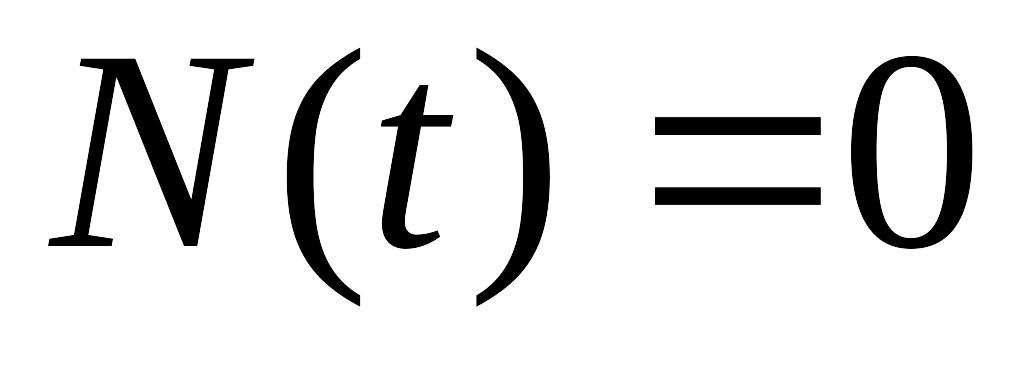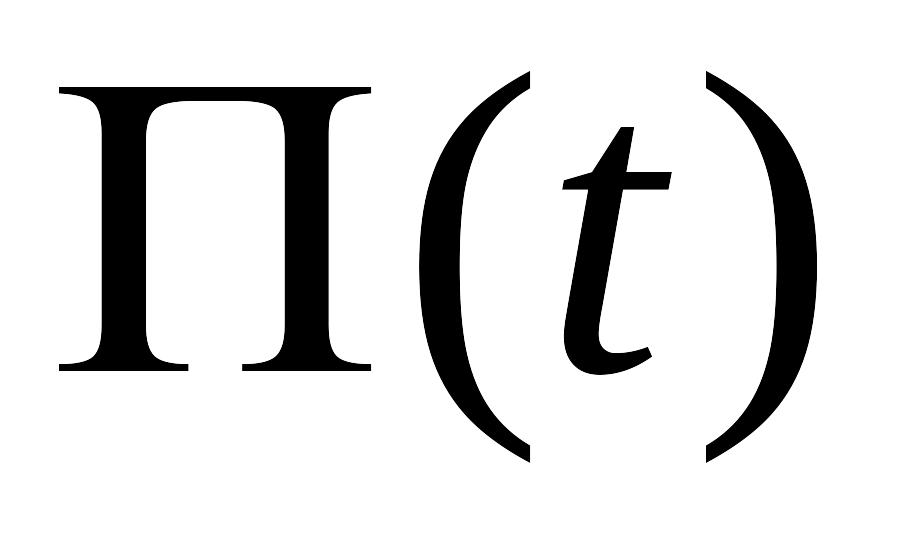– величина всех
премий,
полученных к моменту времени
.
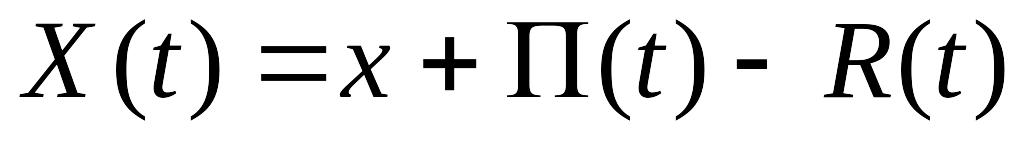определяет капитал
компании к моменту
.
Процессы
и
считаются независимыми. Если
,
то говорят о страховых моделях дискретного
времени,
если
– о моделях непрерывного
времени.
Согласно актуарной
традиции мерой платежеспособности,
или финансовой состоятельности компании,
выбирается
вероятность
неразорения
(соответственно, на бесконечном
и конечном
промежутке времени):
для всех
Поскольку договор страхования предполагает передачу того или иного риска от клиента к компании, то гарантировать исполнение своих обязательств компания может лишь в случае, когда в среднем поступающие премии больше средних выплат по искам:
M(П(t))= M(R(t))
Данное
соотношение предполагается выполненным
для всех рассматриваемых ниже моделей.
Распространенным принципом начисления
премий является принцип математического
ожидания,
когда выбирается некоторое число
,
называемое коэффициентом
нагрузки,
и полагается
.
Введенные
выше вероятности зависят не только от
временного промежутка функционирования
страховой компании и начального капитала,
но и от "внутренних" параметров
процессов
и
.
Тем не менее, ключевой является
зависимость именно от времени
и начального капитала
.
По этим параметрам удается получать
уравнения интегрального (разностного)
и интегро-дифференциального типа для
нахождения вероятностей неразорения,
что позволяет производить количественный
финансовый анализ
экономической деятельности страховой
фирмы.
Часто поиск явного аналитического выражения для решения представляет существенные технические трудности, а получаемые при этом формулы неудобны для дальнейшего анализа. В такой ситуации оказывается полезным иметь адекватные апроксимации для вероятности неразорения.
Рассмотрим биномиальную модель:
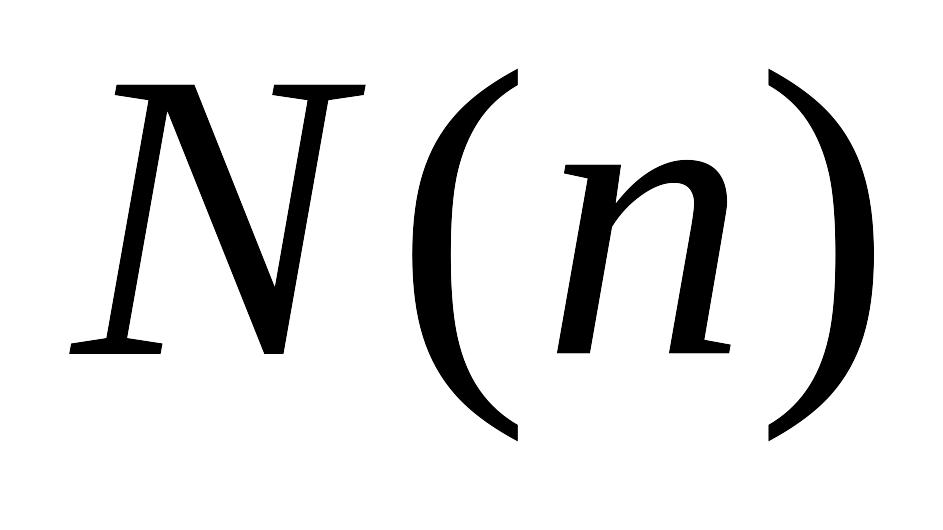– биномиальный
процесс, т. е. представим как сумма
бернуллиевских случайных величин с
некоторой вероятностью успеха
;
(детерминированные
премии);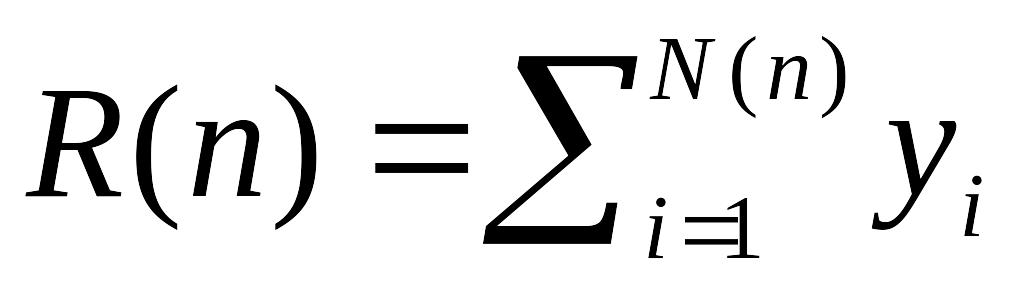
– сложный
биномиальный процесс.
В качестве процесса
премий может рассматриваться независимый
от
другой сложный биномиальный процесс
.
Тогда капитал компании имеет вид
Это означает, что
в каждый момент времени независимым от
прошлого образом с некоторой вероятностью
компания получает, вообще говоря,
случайную премию
,
и с некоторой вероятностью
вынуждена выплачивать величину
.
В случае целочисленных
процессов
для вероятностей неразорения могут
быть получены разностные уравнения,
которые удается разрешить аналитически
для некоторых типов распределений
премий и исков. В
общем случае оценивание вероятности
неразорения может проводиться с помощью
техники мартингалов дискретного времени:
если
– положительное решение характеристического
уравнения
(в
терминах функций распределения
и
случайных величин
и
это уравнение переписывается в виде
то
– мартингал и
.