
Лабораторная работа № 4 Определение длины световой волны с помощью бипризмы
Цель работы: определить длину световой волны из наблюдений интерференционной картины, получаемой с помощью бипризмы.
Краткая теория
 Источники
света называются когерентными, если
они испускают волны одинаковой
частоты и разность фаз колебаний этих
волн не зависит от времени. Лучи света,
испускаемые когерентными источниками,
при наложении будут интерферировать,
что приведет к возникновению светлых
и темных участков во всей области
наложения световых пучков - интерференционной
картине. Результирующая интенсивность
двух интерферирующих волн с интенсивностями
I1
и
I2
равна
Источники
света называются когерентными, если
они испускают волны одинаковой
частоты и разность фаз колебаний этих
волн не зависит от времени. Лучи света,
испускаемые когерентными источниками,
при наложении будут интерферировать,
что приведет к возникновению светлых
и темных участков во всей области
наложения световых пучков - интерференционной
картине. Результирующая интенсивность
двух интерферирующих волн с интенсивностями
I1
и
I2
равна
![]()
г
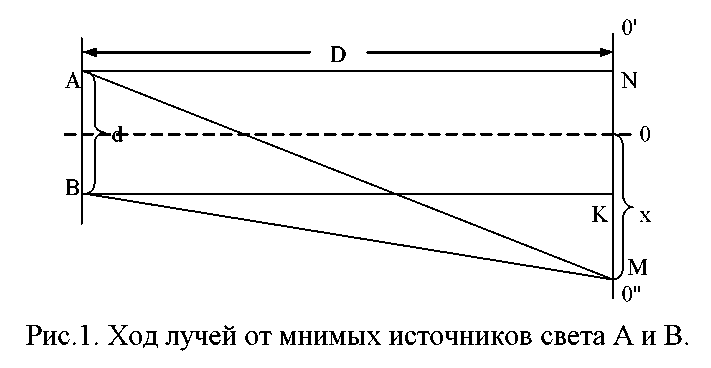
Рис.
1 Ход лучей от мнимых источников
света
А и В![]() - разность
фаз, которую имеют волны в точке
наблюдения. Если разность
фаз
- разность
фаз, которую имеют волны в точке
наблюдения. Если разность
фаз
![]() ,
где m
- любое
целое число, то результирующая
интенсивность
равна нулю (темные участки на
интерференционной картине). При разности
фаз
,
где m
- любое
целое число, то результирующая
интенсивность
равна нулю (темные участки на
интерференционной картине). При разности
фаз
![]() результирующая
интенсивность максимальна (светлые
участки
на интерференционной картине).
результирующая
интенсивность максимальна (светлые
участки
на интерференционной картине).
Разность
фаз двух волн связана с их оптической
разностью хода
![]() соотношением:
соотношением:
![]()
где
![]() -
длина волны интерферирующих лучей. В
точке M
(рис.1)
будет минимум освещенности, если волны
от источников A
и
В
придут
в нее с разностью хода:
-
длина волны интерферирующих лучей. В
точке M
(рис.1)
будет минимум освещенности, если волны
от источников A
и
В
придут
в нее с разностью хода:
![]() (1)
(1)
где n - показатель преломления среды, в которой распространяются волны. При разности хода:
![]() (2)
(2)
в точке М будет наблюдаться максимум освещенности.
Один из методов получения когерентных волн в оптике состоит в делении излучения, испускаемого точечным источником света, тем или иным способом на два потока, которые затем сводятся вместе в некоторой области пространства. В данной работе для разделения волн на два когерентных световых пучка используется бипризма.
Бипризма
состоит из двух призм с малыми преломляющими
углами (около 30’), сложенных одна с
другой короткими сторонами (рис.2). Угол
бипризмы (СОЕ),
обращенный к источнику света близок к
1800.
Источником света служит ярко освещенная
узкая щель, установленная строго
параллельно преломляющему ребру
бипризмы. Вследствие преломления лучей
верхняя половина бипризмы отклоняет
падающий на нее пучок света вниз, а
нижняя половина бипризмы – вверх. Таким
образом, падающий пучок света разделяется
бипризмой на два перекрывающихся пучка,
как бы исходящих из двух мнимых изображений
щели А
и
В.
И
Рис.
2 Разделение бипризмой падающего пучка
света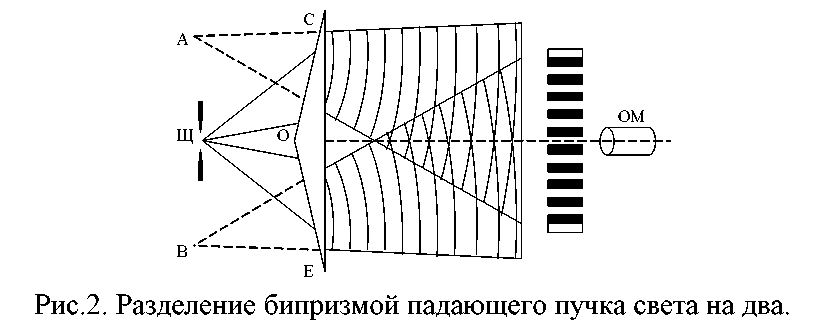 области
наложения световых пучков, испускаемых
этими источниками. Так как все точки
щели эквивалентны, то при монохроматическом
свете источников А
и
В
интерференционная;
картина состоит из ряда светлых
(максимумы) и темных (минимумы) полос,
параллельных щели; ширина a
светлых
и темных полос одинакова. Светлая полоса,
соответствующая разности фаз
интерферирующих лучей
области
наложения световых пучков, испускаемых
этими источниками. Так как все точки
щели эквивалентны, то при монохроматическом
свете источников А
и
В
интерференционная;
картина состоит из ряда светлых
(максимумы) и темных (минимумы) полос,
параллельных щели; ширина a
светлых
и темных полос одинакова. Светлая полоса,
соответствующая разности фаз
интерферирующих лучей
![]() ,
расположена в точке О
(рис.1)
и находится в центре интерференционной
картины. Если источники А
и
В
излучают
белый свет, для каждой длины волны
спектра получается своя система
максимумов и минимумов.
,
расположена в точке О
(рис.1)
и находится в центре интерференционной
картины. Если источники А
и
В
излучают
белый свет, для каждой длины волны
спектра получается своя система
максимумов и минимумов.
Интерференционная картина при этом представляет собой чередующиеся цветные полосы, причем темных полос не будет нигде, т.к. места минимумов для одних длин волн совпадают с местами максимумов для других. Зная расстояние d между мнимыми источниками А и В, расстояние a между интерференционными полосами и расстояние D от щели до плоскости, в которой наблюдают интерференционную картину, можно определить длину волны света, испускаемого источниками.
Для вывода формулы, позволяющей определить длину волны с помощью бипризмы, рассмотрим два когерентных источника света, расположенных в точках А и В (рис.1). Расстояние d между источниками мало по сравнению с расстоянием D до плоскости, в которой наблюдают интерференционную картину. Определим разность хода волн, приходящих в точку М, расположенную на линии O’O’’ (O’O’’ ||АВ) на расстоянии x от точки О.
Из прямоугольных треугольников ANM и BKM имеем:
![]()
![]()
![]()
![]()
![]() ,
поскольку
,
поскольку
![]() и
и
![]() .
Тогда
.
Тогда
![]()
![]()
Расстояние
светлой полосы с номером m
от
центральной, равное xm,
найдем, используя условие максимума
(2)
![]() ,
откуда
,
откуда
![]() .
Положение темных полос
из условия минимума (1)
.
Положение темных полос
из условия минимума (1)
![]() .
Поскольку
ширина светлых и темных
полос одинакова, то расстояние между
соседними светлыми или темными полосами
равно:
.
Поскольку
ширина светлых и темных
полос одинакова, то расстояние между
соседними светлыми или темными полосами
равно:
![]()
Тогда
длина
волны:
![]() (4)
(4)
