3. Градиент функции

Снова рассмотрим формулу производной по направлению:

.

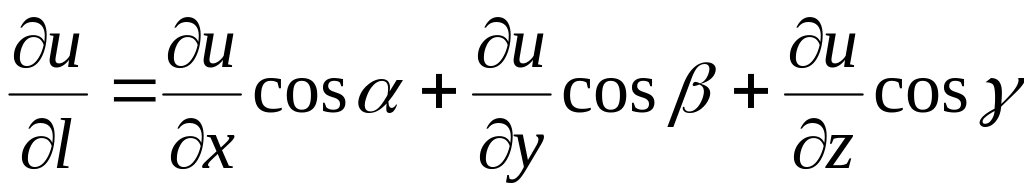Вторые множители в каждом из этих слагаемых являются, как мы уже отмечали, проекциями единичного вектора , направленного по вектору : .

Возьмем теперь вектор, проекциями которого на координатные оси будут служить значения частных производных в выбранной точке . Назовем его градиентом функции и будем обозначать символами:

или .

1. Пусть — однозначная непрерывная функция, имеющая непрерывные частные производные Градиентом скалярной функции называется вектор, проекции которого на координатные оси Ох, Оу и Oz соответственно равны значениям частных производных этой функции , т. е.

.

На основании этого определения проекции вектора на координатные оси запишутся так:

; ; .

Модуль вектора вычисляется по формуле:

.

Подчеркнем, что проекции градиента зависят от выбора точки и изменяются с изменением координат этой точки. Таким образом, каждой точке скалярного поля, задаваемого функцией поля , соответствует определенный вектор – градиент этой функции.

Связь градиента с производной по направлению

Из определения градиента следует, что производная функции по данному направлению равна скалярному произведению градиента функции на единичный вектор этого направления:

.

Из определения скалярного произведения:

,

где  - угол между и . Отсюда видно, что производная по направлению достигает наибольшего значения, когда , т.е. при =0. Причем это наибольшее значение .

Итак, направление градиента есть направление наискорейшего возрастания функции.

Свойства градиента

1) Из всех производных функции, взятых по различным направлениям, наибольшее значение всегда имеет производная по направлению градиента функции. Поэтому есть вектор скорости наибыстрейшего возрастания функции. При этом равен числовому значению наибольшей скорости изменения скалярного поля.

2) Скалярное поле убывает быстрее всего в направлении, противоположном вектору , со скоростью, равной .

3) Вектор в каждой точке направлен по нормали к поверхности (или линии) уровня поля, проходящей через эту точку, в сторону возрастания функции.

Скорость изменения скалярной функции по некоторому направлению равна проекции вектора на это направление , т. е.

.

В этом состоит основное свойство градиента функции.

Из последнего свойства вытекает, что производная по любому направлению, касательному к поверхности уровня, проходящей через данную точку, равна нулю.

Геометрический смысл градиента. С точки зрения геометрического представления градиент перпендикулярен поверхности уровня функции.

Физический смысл градиента. Градиент – вектор, показывающий направление наискорейшего изменения некоторого скалярного поля u в какой-либо точке (градиент температуры, градиент давления и т.п.).

При вычислениях применяют следующие свойства градиента:

.

Примеры.

1. С какой наибольшей скоростью может возрастать функция при переходе точки через точку ? В каком направлении должна двигаться точка М при переходе через точку , чтобы функция убывала с наибольшей скоростью?

Наибольшая, по абсолютной величине, скорость изменения функции при переходе точки М через точку Р численно равна модулю градиента функции в точке Р. При этом функция будет возрастать или убывать с наибольшей скоростью, смотря по тому, будет ли точка М при переходе через точку Р двигаться по направлению градиента функции в точке Р или по прямо противоположному направлению. Руководствуясь этими положениями, находим частные производные функции и ее градиент в любой точке:

(2)

Далее находим градиент в указанных точках, подставив их координаты в выражение (2):

1) ,

его модуль, численно равный искомой наибольшей скорости возрастания данной функции при переходе М через точку М₀, равен:

.

2) ,

Искомый вектор, имеющий прямо противоположное направление, будет

.

Чтобы функция убывала с наибольшей скоростью, при переходе через точку М₁ точка М должна двигаться в направлении вектора .

1 Предполагается, что функция — однозначная непрерывная функция , имеющая непрерывные частные производные первого порядка , , .