
Преобразование Лапласа. Оригинал и изображение
Преобразование Лапласа функции
![]() которая может принимать комплексные
значения, называется функция
которая может принимать комплексные
значения, называется функция![]() комплексного переменногор,
определяемая следующим равенством:
комплексного переменногор,
определяемая следующим равенством:![]() (2.1). Функция
(2.1). Функция![]() называется оригиналом, если она
удовлетворяет условиям: 1)
называется оригиналом, если она
удовлетворяет условиям: 1)![]() ;
2) существуют также постоянные М иS,
что
;
2) существуют также постоянные М иS,
что![]() (infS=S0называется показателем роста функции
(infS=S0называется показателем роста функции![]() ;
3) на любом конечном отрезке [0,T]
функция
;
3) на любом конечном отрезке [0,T]
функция![]() имеет не более чем конечное число точек
разрыва первого рода, причем считаем,
что
имеет не более чем конечное число точек
разрыва первого рода, причем считаем,
что![]() .
.
Функцию
![]() называют
изображением для
называют
изображением для![]() и при этом записывается
и при этом записывается![]() или
или![]() .
.![]() является функцией, заданной в полуплоскостиRep>S0.
Простейшей функцией оригиналом является
единичная функция Хевисойде (рис 2.1)
является функцией, заданной в полуплоскостиRep>S0.
Простейшей функцией оригиналом является
единичная функция Хевисойде (рис 2.1)
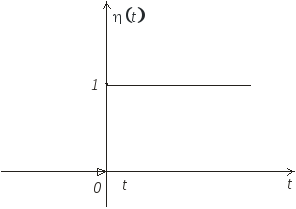
рис. 2.1
![]()
В дальнейшем для сокращения записи
будем, как правило, писать
![]() ,
считая, что
,
считая, что![]() .
Ниже приводятся основные теоремы
операционного исчисления.
.
Ниже приводятся основные теоремы
операционного исчисления.
1) Свойство линейности.
Для постоянной![]()
![]() (2.2) (Здесь и всюду в дальнейшем считаем,
что
(2.2) (Здесь и всюду в дальнейшем считаем,
что![]() );
);
2) теорема подобия.
Для любой постоянной
![]()
3)Теорема смещения.Умножение
оригинала на![]() соответствует запаздыванию изображения
на
соответствует запаздыванию изображения
на![]() ,
т.е.
,
т.е.
![]() (2.4)
(2.4)
![]() - некоторая постоянная (действительная
или комплексная величина).
- некоторая постоянная (действительная
или комплексная величина).
4)Теорема запаздывания.Запаздыванию включения оригинала на![]() соответствует умножению изображения
на
соответствует умножению изображения
на![]() ,
т.е.
,
т.е.
![]() (2.5)
(2.5)
(при
![]() в силу первого условия, налагаемого на
оригинал,
в силу первого условия, налагаемого на
оригинал,![]() ).
).
5)Теорема о дифференцировании оригинала.
Если
![]() и ее производные
и ее производные![]() являются оригиналами, то для любого
являются оригиналами, то для любого![]()
![]() (2.6)
(2.6)
В частности
![]() (2.7)
(2.7)
6)Интегрирование
оригинала.Интегрирование оригинала
сводится к делению изображения на![]() ,
т.е.
,
т.е.
![]() .
(2.8)
.
(2.8)
7)Дифференцирование изображения.
Если
![]() ,
то
,
то![]() ,
в общем случае
,
в общем случае![]() (2.9)
(2.9)
Задача 1.
Выяснить, какие из данных функций являются оригиналами:
а)
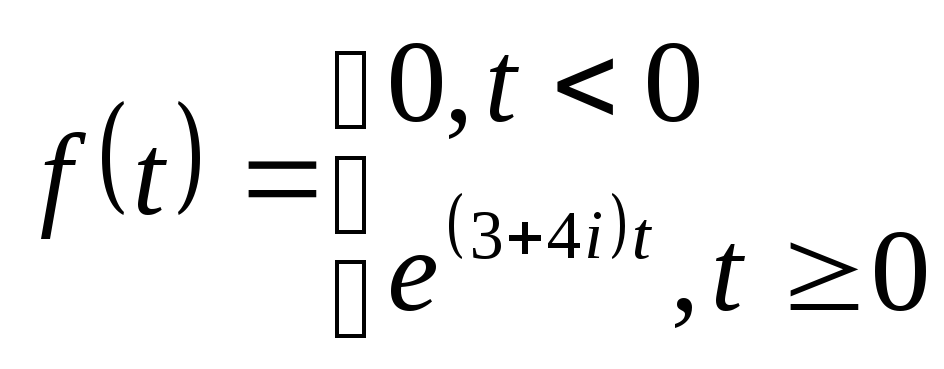 б)
б)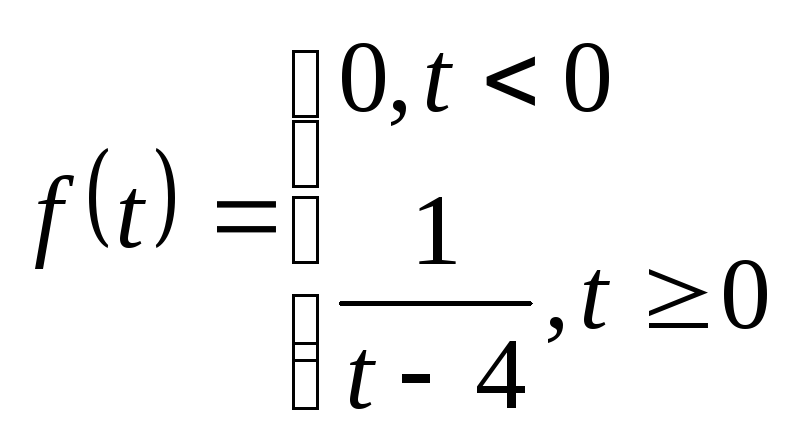
Решение.а) функция![]() является оригиналом, т.к. удовлетворяет
всем требования, предъявляемым к
оригиналу: при
является оригиналом, т.к. удовлетворяет
всем требования, предъявляемым к
оригиналу: при![]() обращается в нуль, непрерывна, а для
обращается в нуль, непрерывна, а для![]()
![]() при
при![]() ;
;
б) функция
![]() не является оригиналом, т.к. в точке
не является оригиналом, т.к. в точке![]() ,
принадлежащей промежутку
,
принадлежащей промежутку![]() ,
она имеет разрыв второго рода.
,
она имеет разрыв второго рода.
Задача 2.Найти изображение функций-оригиналов, используя определение:
а)
![]() ;
б)
;
б)![]() .
.
Решение.Для функции![]() имеем
имеем
![]() ,
,
так как
![]()
![]() при
при![]() .
.
Для функции
![]() имеем
имеем
![]() при
при![]() .
.
Задача 3.Найти изображения следующих функций-оригиналов, используя теоремы операционного исчисления.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
д)
;
д)![]() .
.
Решение.а) Имеем![]() .
Используя теорему смещения для
.
Используя теорему смещения для![]()
и окончательно, учитывая свойство линейности (2.2), запишем
![]() ;
;
б) для функции
![]() используем теорему о дифференцировании
изображения;
используем теорему о дифференцировании
изображения;
если
![]() ,
то
,
то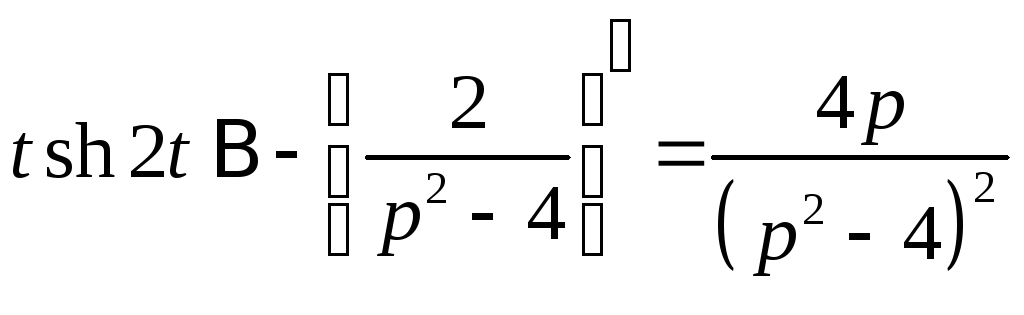 ;
;
в) имеем
![]() .
.
Применяя теорему смещения к
![]() и
и![]() и используя свойство линейности (2.2),
получаем
и используя свойство линейности (2.2),
получаем
![]() ;
;
г) для функции
![]() воспользуемся результатом предыдущего
примера и теоремой смещений (2.4):
воспользуемся результатом предыдущего
примера и теоремой смещений (2.4):
если
![]() ,
то
,
то![]() ;
;
д)
![]() .
Найти
.
Найти![]() .
.
Если
![]() ,
то
,
то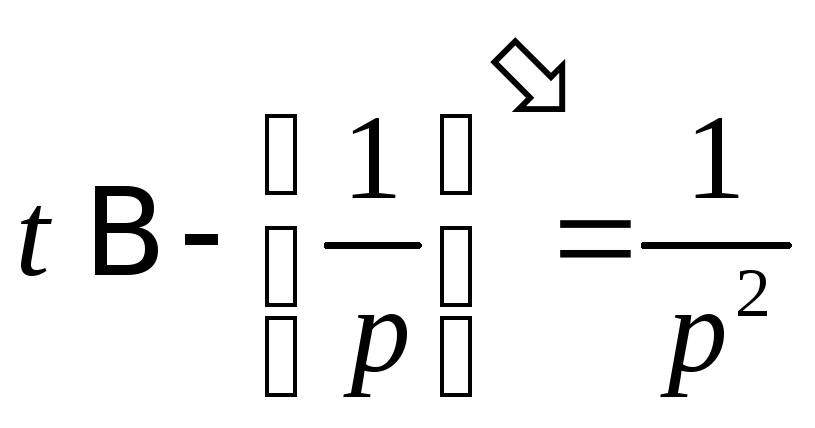 ;
далее для
;
далее для![]() .
.
Ниже приводится таблица основных операционных соотношений.
Таблица.
|
№ п/п |
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
Задача 4.Найти изображение следующих функций-оригиналов, используя теоремы операционного исчисления и таблицу.
а)
![]() ;
;
б)
![]() ;
в)
;
в)![]() .
.
Решение.а) используя свойство линейности и таблицу, получи
![]() ;
;
б) применив формулу, получим
![]()
и используя свойство линейности, можем записать
![]() ;
;
в) учитывая соотношение
![]() и теорему смещения
и теорему смещения
![]()
![]() ,
получим
,
получим![]() .
.
Задача 5.Найти изображение для функции-оригинала, представленного графически (рис. 2.2).


Решение. Имеем
![]() .
.
Это эквивалентно записи
![]()
И теперь, используя теорему запаздывания, таблицу и свойство линейности, получим
![]() .
.
