
Решение.
Воспользуемся признаком сравнения.
Общий
член исходного ряда
![]() :
:
![]() .
.
Учитывая,
что для больших значений
![]() :
:
![]() ,
то сравним исходный ряд с рядом
,
то сравним исходный ряд с рядом
![]() ,
общий член которого равен
,
общий член которого равен
![]() .
.
Вычислим предел:
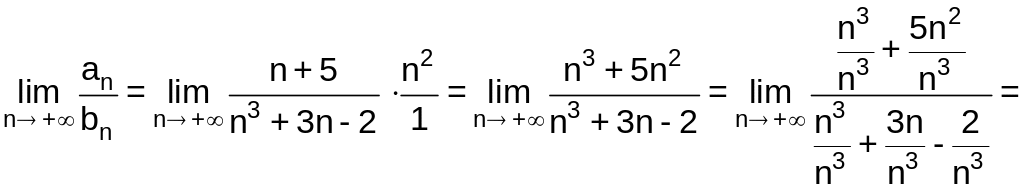
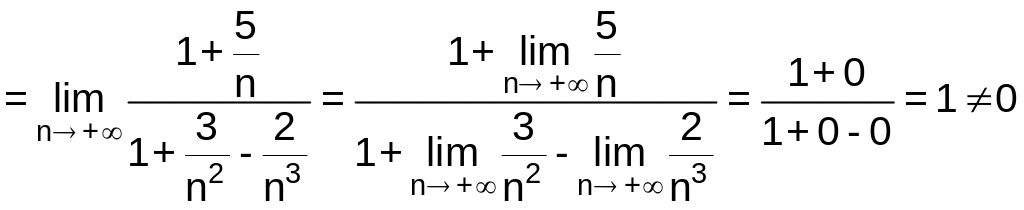 .
.
Так как значение предела не равно 0, то оба ряда являются сходящимися или расходящимися.
Заметим,
что обобщенный
гармонический ряд
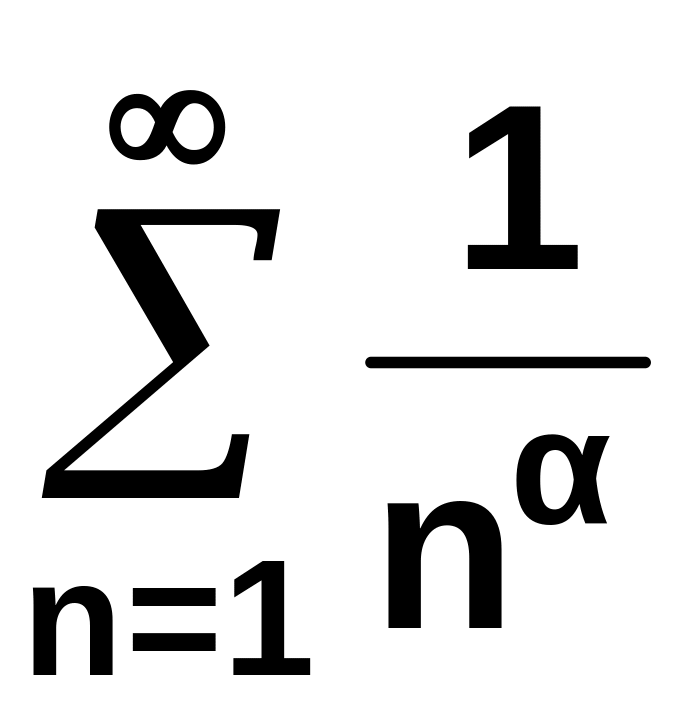 является
сходящимся, если
является
сходящимся, если
![]() и расходится, если
и расходится, если
![]() .
.
Так
как ряд
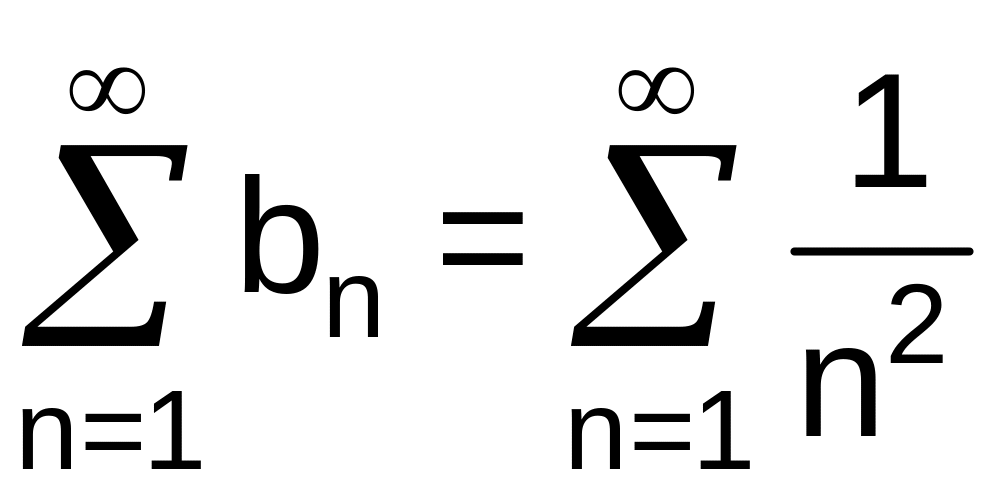 сходится
сходится
![]() ,
то и исходный ряд сходится.
,
то и исходный ряд сходится.
Ответ: ряд сходится.
б)
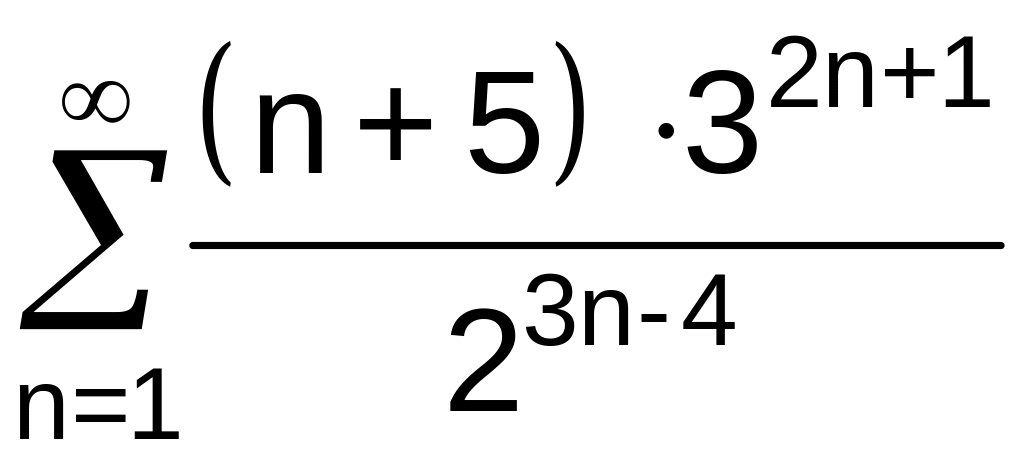 .
.
Решение.
Воспользуемся признаком Д’Аламбера.
Определим
![]() и
и
![]() члены ряда:
члены ряда:
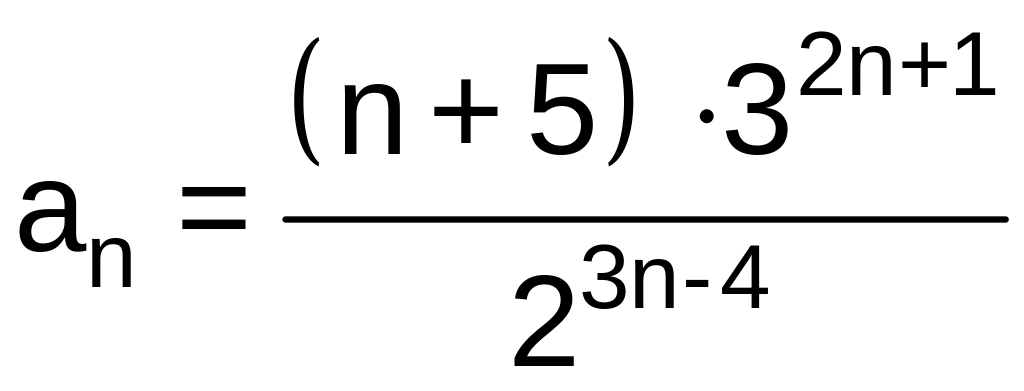 и
и
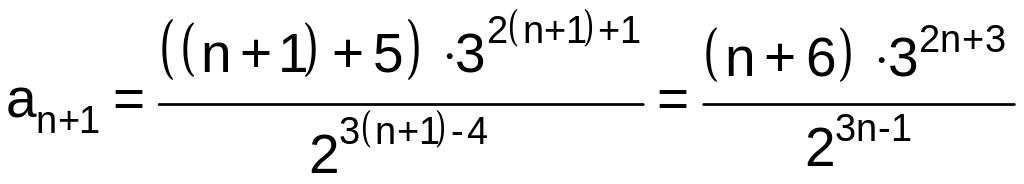 .
.
Вычислим предел:
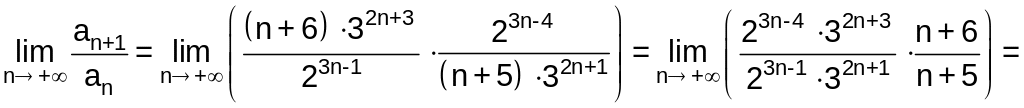
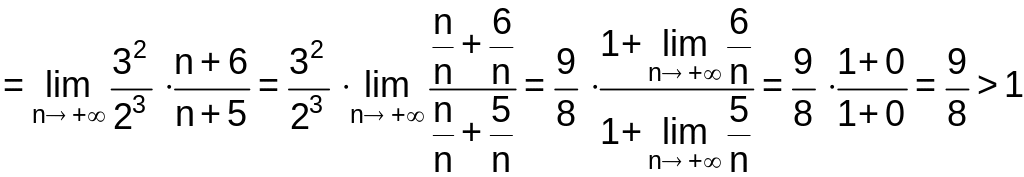
Ряд расходится, так как значение предела больше 1.
Заметим, что если значение предела меньше 1, то ряд сходится.
Ответ: ряд расходится.
№12.
Исследовать
сходимость ряда:а)
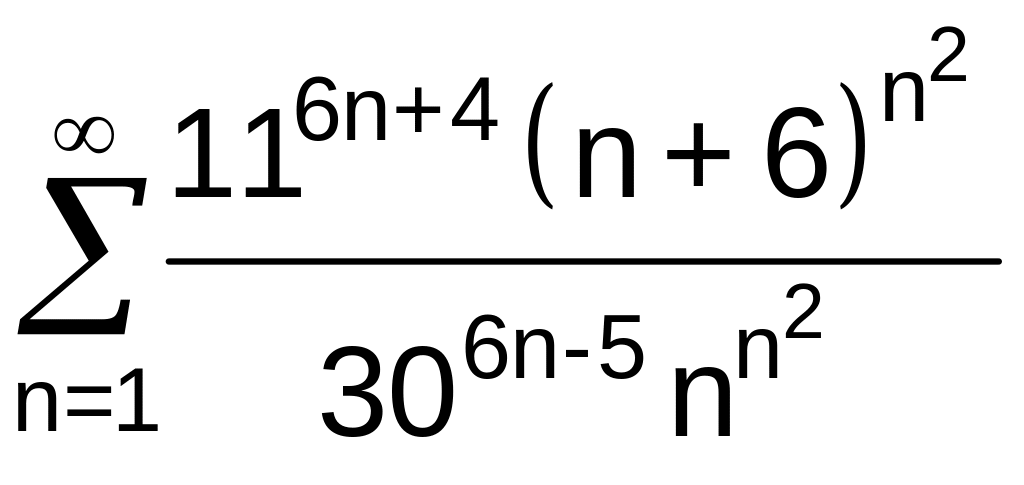 .
.
Решение.
Воспользуемся признаком Коши.
Общий
член ряда
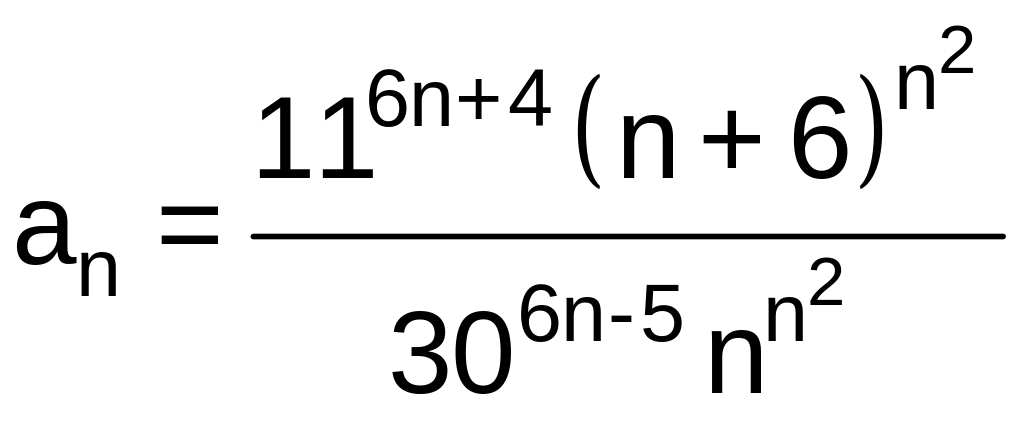 .
.
Вычислим предел:
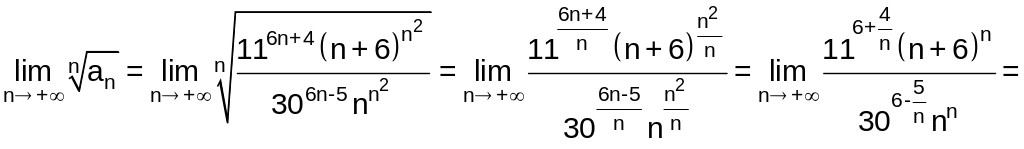
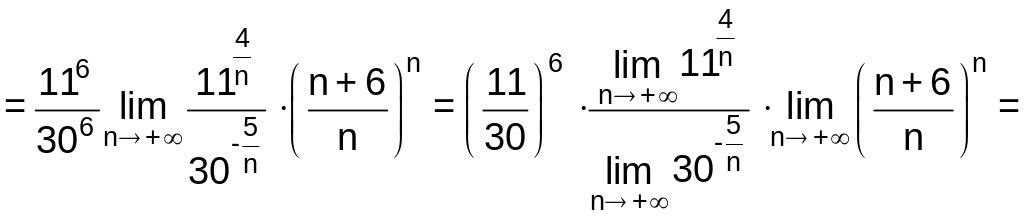
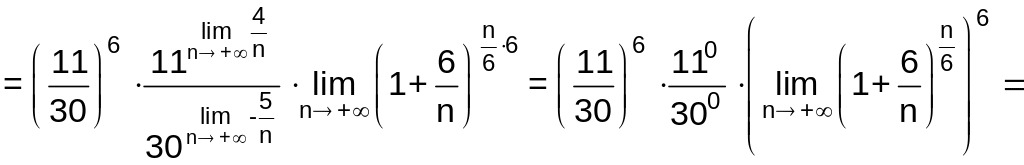
 ,
так
как
,
так
как
![]() .
.
Ряд сходится, так как значение предела меньше 1.
Заметим, что если значение предела больше 1, то ряд расходится.
Ответ: ряд сходится.
б) .
Решение.
Исходный
ряд является
знакочередующимся рядом
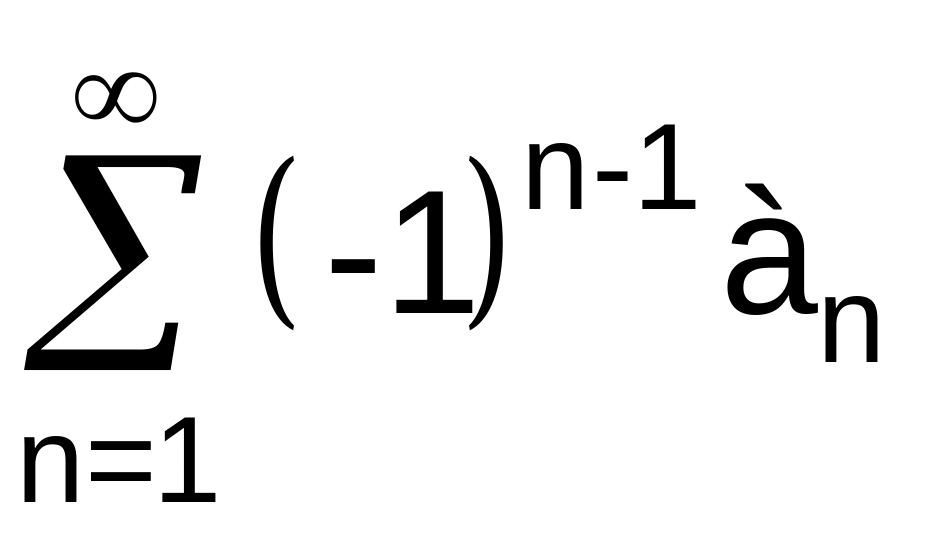 ,
где
,
где
![]() .
Воспользуемся следствием признака
Лейбница о сходимости таких рядов: если
члены знакочередующегося ряда
.
Воспользуемся следствием признака
Лейбница о сходимости таких рядов: если
члены знакочередующегося ряда
 ,
,
![]() ,
монотонно убывают
,
монотонно убывают
![]() ,
начиная с некоторого номера
,
начиная с некоторого номера
![]() ,
и стремятся к нулю
,
и стремятся к нулю
![]() ,
то ряд сходится.
,
то ряд сходится.
Очевидно,
что
![]() .
.
Вычислим предел:
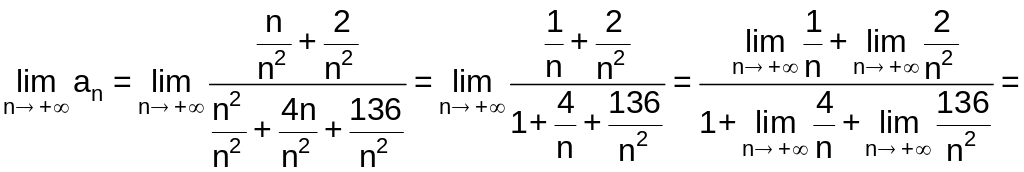
![]() .
.
Так как , то
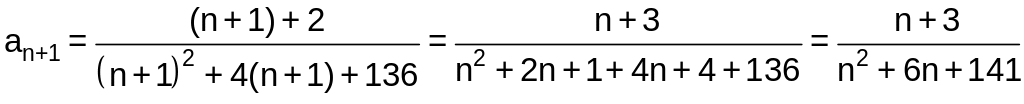 .
.
Решим
неравенство:
![]() ,
т.е.
,
т.е.
![]()
Тогда
![]() и
и
![]()
![]()
![]() .
.
Следовательно,
![]() и
и
![]() .
.
Разложим
левую часть неравенства на множители.
Для этого решим уравнение
![]() ,
дискриминант которого равен
,
дискриминант которого равен
![]() .
.
Откуда
![]() и
и
![]() .
.
Таким
образом
![]() или
или
![]() и неравенство
выполняется для любого натурального
и неравенство
выполняется для любого натурального
![]() .
.
Следовательно, исходный ряд является сходящимся.
Ответ: ряд сходится.
№13.
Найти область сходимости степенного
ряда:
 .
.
Решение.
Исходный
ряд является степенным рядом вида
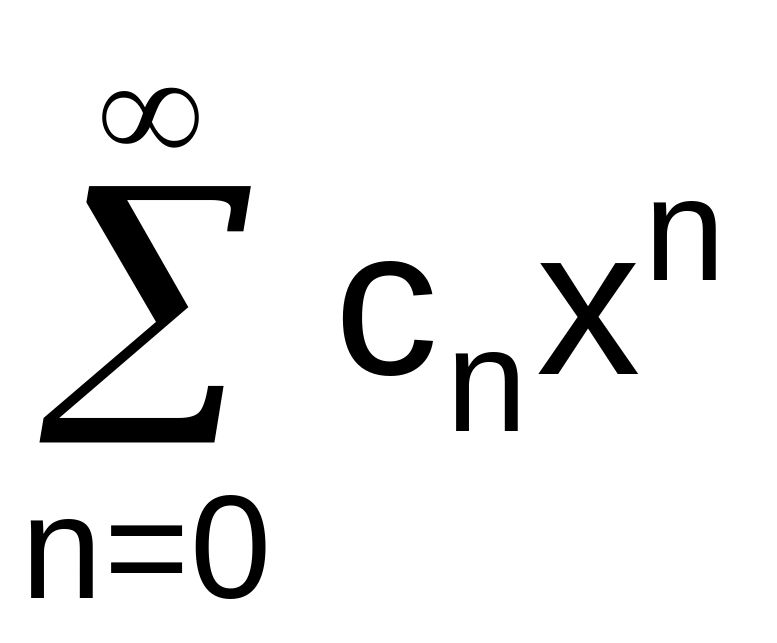 ,
где
,
где
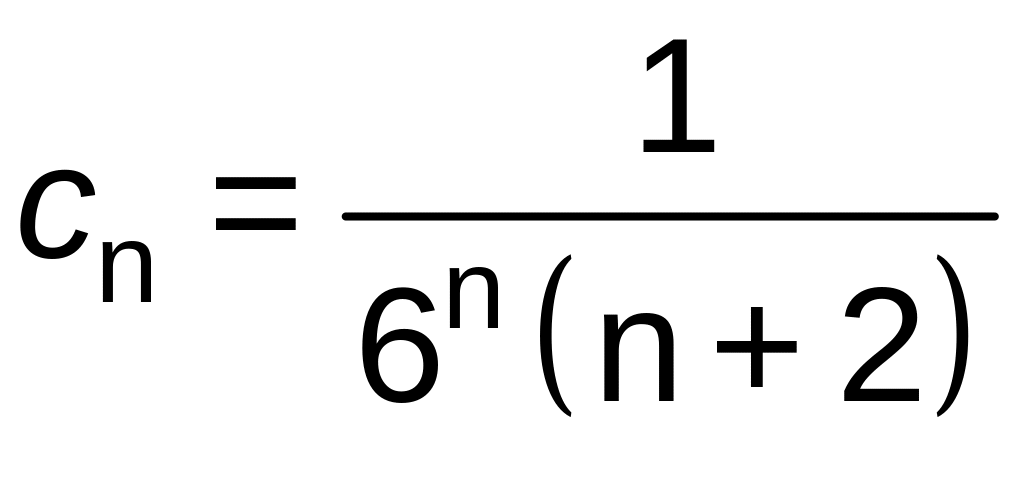 .
.
Тогда
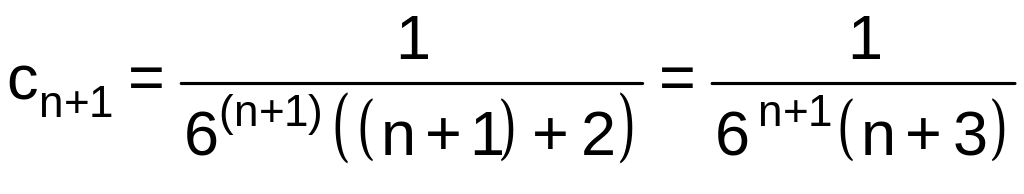 .
.
Вычислим радиус сходимости степенного ряда:
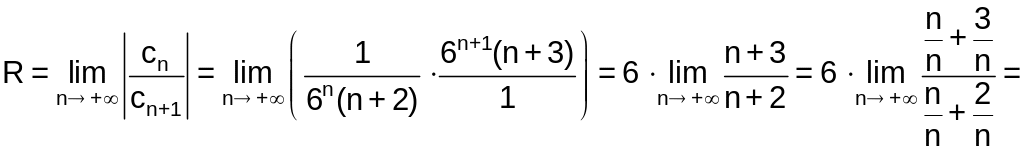
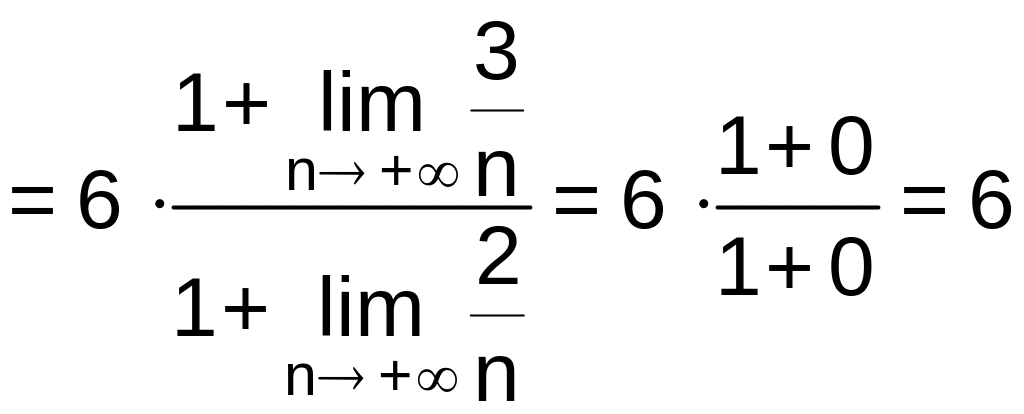 .
.
Следовательно,
![]() ,
т.е.
,
т.е.
![]() интервал
сходимости ряда.
интервал
сходимости ряда.
Если,
![]() ,
то получим ряд
,
то получим ряд
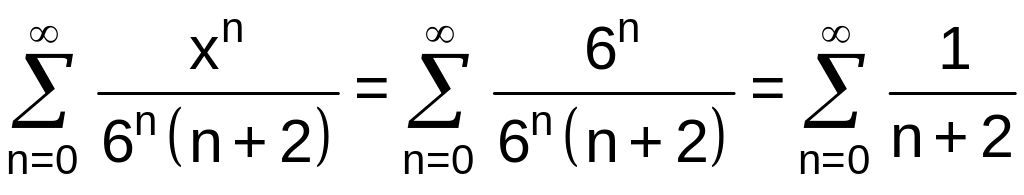 ,
,
который
расходится, как и гармонический ряд
![]() .
.
Если,
![]() ,
то получим ряд
,
то получим ряд
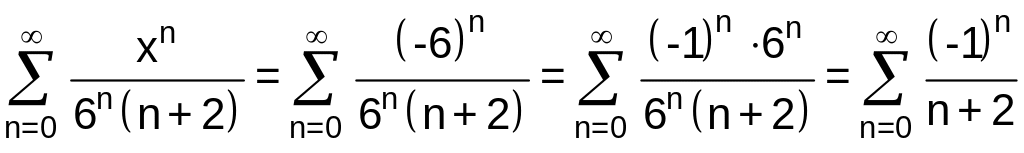 .
.
Полученный
ряд сходится, как знакочередующийся
ряд
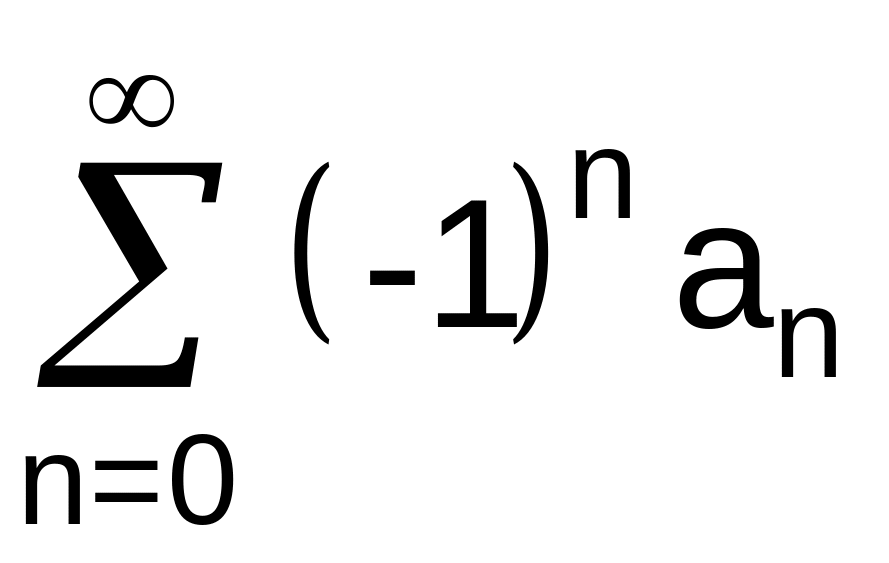 ,
где
,
где
![]() ,
так как
,
так как
![]() ,
то
,
то
![]() ,
,
и
![]()
- монотонно убывающая последовательность.
Таким
образом,
![]()
область
сходимости
степенного ряда.
область
сходимости
степенного ряда.
Ответ: .
