Определите план перевозок железной руды на обогатительные фабрики, который обеспечивает минимальные совокупные транспортные издержки, предварительно построив модель.

40. Три пекарни осуществляют ежедневные поставки хлеба для 4 магазинов. Найдите распределение поставок из каждой пекарни, минимизирующее транспортные затраты.

Пекарня	Транспортные затраты на единицу продукции				Предло- жение
	Магазин 1	Магазин 2	Магазин 3	Магазин 4
А	1,5	2,5	1	2	700
В	2	3	2	1	650
С	1	1,5	2,5	3	800
Спрос	400	500	350	10000

41. Фирма по прокату автомобилей «Золотое кольцо России» собирает заявки на аренду во всех городах центра России. Клиент имеет возможность получить автомобиль в любом удобном для него населенном пункте и оставить его в любом месте, где он заканчивает путешествие, в том числе и в своем родном городе. Работники фирмы забирают оставленные автомобили и перегоняют их для передачи новым клиентам.

Сейчас 4 автомобиля компании оставлены в Клину, 3 – в Ростове Великом, 6 – в Ярославле и 1 – в Серпухове. Имеются заказы на 5 автомобилей во Владимире, на 3 автомобиля в Санкт-Петербурге и на 6 автомобилей в Москве. Расстояния между городами (в км) приведены в следующей таблице:

Составьте план, по которому надо перегонять автомобили новым клиентам, ориентируясь на минимальное расстояние, которое пройдут все перегоняемые автомобили. Сколько автомобилей следует перегнать в Москву из Ярославля?

42. Предприятие розничной торговли имеет четыре крупных универмага, расположен­ных в различных городах — Р, Q, R, S. Поставки продукции в эти универмаги осуществляются с двух торговых складов А и В, площади которых вмещают по 40 единиц продукции ежедневно.

В будущем планируется расширить площади универмагов, поэтому их потреб­ности в продукции с торговых складов составят 27, 25, 30 и 35 единиц в день соответственно. Чтобы удовлетворить текущий и будущий спрос, планируется построить третий склад, площади которого позволят хранить в нем 60 единиц продукции ежедневно. Рассматриваются два варианта его размещения. Ниже приведены транспортные издержки, соответствующие перевозке продукции с двух существующих складов, и два варианта размещения нового склада.

Торговый склад	Транспортные издержки, ден. ед./ед
	Р	Q	R	S
А	70	85	55	120
В	110	90	75	110
Вариант 1	115	115	70	90
Вариант 2	135	95	80	75

Требуется оценить транспортную модель и принять решение о том, какой вариант размещения нового склада лучше.

43. Уголь добывается на 5 шахтах, показатели объемов выпуска и издержек производства которых приведены в таблице 1.

Таблица 1 Таблица2

Шахта	Объем добычи, т/день	Издержки производства, ден. ед./т	Завод	Выпуск продукции, т/день	Эксплуатац. Расходы, ден. ед./т
1 2 3 4 5	120 150 80 160 140	25 29 34 26 28	А В С	300 200 200	2 3 3

До того, как уголь будет готов к продаже, его надо «очистить» и отсортировать на одном из трех углеперерабатывающих заводов. В табл. 2 приведены значения производственных возможностей и эксплуатационных расходов по каждому заводу.

Перевозка угля осуществляется по железной дороге, ее стоимость равна 0,5 ден. ед. за 1 т-км. Расстояние от каждой шахты до каждого углеперерабатывающего завода – в табл. 3.

Таблица 3

Углеперерабатывающий завод	Шахта
	1	2	3	4	5
А	22	44	26	52	24
В	18	16	24	42	48
С	44	32	16	16	22

1) Построив транспортную модель, определите, как следует распределить перевозки добытого угля с шахт на каждый из трех перерабатывающих заводов.

2) Ввиду установки нового оборудования на шахте 3 ее издержки производства, как ожидается, снизятся до 30 ден. ед. за 1 т. Окажет ли это изменение воздействие, и если да, то какое, на распределение перевозок угля на перерабатывающие заводы?

3) Планируется увеличение объема добычи на шахте 5 до 180 т в день, причем его можно достичь, не увеличивая издержки производства 1 т угля. Как это повлияет на распределение перевозок угля к перерабатывающим заводам?

НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

44. Примером классической задачи математического программирования является задача об определении опти­мального размера партии товара в теории управления запасами. Имеющийся у фирмы запас некоторого одно­родного товара I(t) уменьшается с постоянной скоростью dI/dt, т. е. в каждую единицу времени используется одно и то же количество товара. Фирма производит заказы на некоторое количество этого товара х, которое поставляется ей немедленно всякий раз, когда уровень запасов стано­вится равным нулю. Ежегодная потребность в товаре рав­на А, и фирма производит заказы на поставку ей новых партий товара п раз в течение года, так что А = пх.

При хранении товара фирма несет убытки, связанные с расходами на хранение товара и оформление заказов. Средняя величина запаса товара равна , а расходы на хранение одной единицы товара равны С_h, так что общие расходы на хранение составляют C_h . Как сказано выше, фирма производит заказы на поставку новых пар­тий товара п раз в течение года. Расходы на оформление одного отдельного заказа равны С_о, поэтому общие рас­ходы на оформление заказов равны С₀п. Таким образом, общие расходы составляют С = C_h + С₀п.

1. Минимизировать общие расходы на хранение товара С, выбирая х и п при условии, что А = пх. (Указание: воспользоваться методом множителей Лагранжа.)

2. Найдите оптимальную величину поставки (оптимальное значение х) как функцию параметров С_о, С_h и А. Объясните, какой смысл имеет множитель Лагранжа в данной задаче.

3. Третий вид расходов фирмы составляют штрафные платежи за невыполненные ею заказы. Этот вид расходов ранее не упоминался, поскольку предполагалось, что у фирмы всегда имеется нужный запас товаров. Предположим теперь, что фирма производит заказы даже не при нулевом уровне запасов, а только тогда, когда уровень не выполненных ею заказов дос­тигает определенного значения U, и что в этот момент она производит все необходимые поставки своим заказчикам. Стоимость одного невыполнен­ного заказа равна С_р. Найти оптимальные уровни х и U.

45. Клиент поручил брокерской конторе купить для него на 1 млн. руб. акции трех известных компаний. Сделка заключалась на год. Клиент заинтересован, с одной стороны, в максимизации средней прибыли на вложенный капитал, а с другой – в минимизации риска, поскольку прибыль, получаемая в конце года от акций каждой компании, является случайной величиной. Известно, что чем прибыльнее акции, тем выше связанный с ней риск, поэтому названные критерии являются противоречивыми. Клиенту это обстоятельство разъяснили и попросили его указать относительную значимость («вес») критериев. Клиент, будучи человеком осторожным, высказал пожелание, чтобы риск учитывался с весом втрое большим, чем прибыль. Получив такие указания, сотрудники брокерской конторы сформулировали следующую модель нелинейного программирования:

;

Первая сумма в критерии – ожидаемое значение прибыли, обеспечиваемой пакетом акций, вторая – дисперсия прибыли (мера риска) пакета акций, взятая с «весом» 3. Пусть средняя норма прибыли акций составляет соответственно 8, 10 и 13 %. Дисперсии и ковариации доходностей акций равны: σ₁₁ ═ 0,1, σ₂₂ ═ 0,15, σ₃₃ ═ 0,19, σ₁₂ ═ 0,01, σ₁₃ ═ 0,02, σ₂₃ ═ 0,03.

Найдите оптимальную структуру портфеля ценных бумаг.

46. По плану производства продукции предприятию необходимо изготовить 200 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве Х₁ изделий первым способом затраты равны 8Х₁² + Х₁ грн., а при изготовлении Х₂ изделий II способом они составляют Х₂² + 4Х₂ грн. Определите, сколько изделий каждым способом следует изготовить, чтобы общие затраты на производство продукции были минимальными.

47. Владелец небольшого предприятия располагает на ближайший месяц 100 тыс. руб., которые он может потратить на увеличение основных фондов К (закупку оборудования) по цене 1000 руб. за единицу либо на покупку дополнительной рабочей силы L по цене 50 руб./ч. Увеличение объема готовой продукции, которая может быть продана по 10 тыс. руб. за единицу, определяется производственной функцией . Сколько средств следует потратить на увеличение основных фондов?

48. Определите, в каком количестве необходимо добывать сырье видов А и В, чтобы получаемая прибыль была максимальной. Трудоемкость и прибыль выражены нелинейными функциями количества добываемого сырья. Аналитические зависимости для этих функций в интервале 0  х _j  2 (j = 1, 2) сведены в таблицу.

Сырье	А	В	Ресурс
Добыто	х 1	х 2
Трудоемкость	2х21	3х22	6
Прибыль, тыс. грн.	2х1 – х21	х2

49. Распределить заказ на изготовление однородного продукта в количестве 100 единиц между тремя предприятиями так, чтобы получит максимальную прибыль, если известно, что прибыль, получаемая j-м предприятием от реализации х_j единиц произведенного продукта, представляется в виде следующей функции:

где а₁ = 2; а₂ = 2,5; а₃ = 3; b₁ = 0,8; b₂ = 0,7; b₃ = 0,6.

50. Банк имеет возможность выделить 10 ден. ед. на фор­мирование портфеля акций. Ценные бумаги можно приобрести у компа­ний К_х, К_г и К₃. Номинальная стоимость акции компании К_г составляет 3 ден. ед., компании К₂ - 2 ден. ед., компании К₃ - 5 ден. ед. На конец года рынок ценных бумаг может оказаться в одном из двух состояний С_: и С₂. Эксперты установили, что дивиденды компании К_х для состояния С₁ на конец года составят 10% от номинальной стоимости акции, а для со­стояния С - 15%; для компании К соответственно 8 и 12%; для компа­нии К₃ - 14 и 8%.

Сформировать портфель акций банка, обеспечив ему возможно боль­шую прибыль.

ТЕОРИЯ ИГР И ПРИНЯТИЕ РЕШЕНИЙ

51. Вы можете вложить деньги в три инвестиционных фонда открытого типа: простой, специальный (обеспечивающий максимальную долгосрочную прибыль от акций мелких компаний) и глобальный. Прибыль от инвестиции может меняться в зависимости от условий рынка. Существует 10%-я вероятность, что ситуация на рынке ценных бумаг ухудшится, 50%-я – что рынок останется умеренным и 40%-я – рынок будет возрастать. Следующая таблица содержит значения процентов прибыли от суммы инвестиций при трех возможностях развития рынка.

Альтернатива (фонды)	Процент прибыли от инвестиций
	Ухудшающийся рынок	Умеренный рынок	Растущий рынок
Простой	+5	+7	+8
Специальный	-10	+5	+30
Глобальный	+2	+7	+20

1. Представьте задачу в виде дерева решений.

2. Какой фонд открытого типа следует выбрать?

52. Вы имеете возможность вложить деньги либо в 7,5%-е облигации, которые продаются по номинальной цене, либо в специальный фонд, который выплачивает лишь 1% дивидендов. Если существует вероятность инфляции, процентная ставка возрастет до 8% , и в этом случае номинальная стоимость облигаций увеличится на 10%, а цена акций фонда – на 20%. Если прогнозируется спад, то процентная ставка понизится до 6%. При этих условиях ожидается, что номинальная стоимость облигаций поднимется на 5%, а цена акций фонда увеличится на 20%. Если состояние экономики останется неизменным, цена акций фонда увеличится на 8%, а номинальная стоимость облигаций не изменится. Экономисты оценивают в 20% шансы наступления инфляции и в 15% - наступление спада. Ваше решение относительно инвестиций принимается с учетом экономических условий следующего года.

1. Представьте задачу в виде дерева решений.

2. Что вы будете покупать: акции фонда или облигации?

53. Фирма планирует производство новой продукции быстрого питания в национальном масштабе. Исследовательский отдел убежден в большом успехе новой продукции и хочет внедрить ее немедленно, без рекламной кампании на рынках сбыта фирмы. Отдел маркетинга положение вещей оценивает иначе и предлагает провести интенсивную рекламную кампанию. Такая кампания обойдется в 100 тыс. долларов, а в случае успеха принесет 950 тыс. долларов годового дохода. В случае неудачи рекламной кампании (вероятность этого составляет 30%) годовой доход оценивается лишь в 200 тыс. долларов. Если рекламная кампания не проводится вовсе, то годовой доход оценивается в 400 тыс. долларов при условии, что покупателям понравится новая продукция (вероятность этого равна 0,8) и в 200 тыс. долларов с вероятностью 0,2, если покупатели останутся равнодушными к новой продукции.

1. Представьте задачу в виде дерева решений.

2. Как должна поступить фирма?

3. Пусть дирекция компании решила провести пробную продажу своей продукции в выбранных населенных пунктах. Результатом пробной продажи являются оценки «хорошо» (а₁) или «плохо» (а₂). Тест дает следующие условные вероятности с проведением рекламной кампании и без нее.

С рекламной кампанией Без рекламной кампании

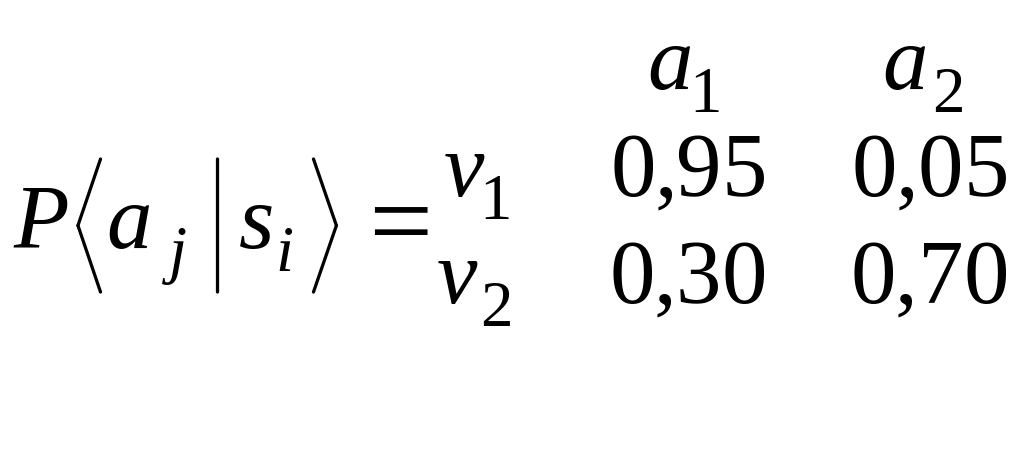
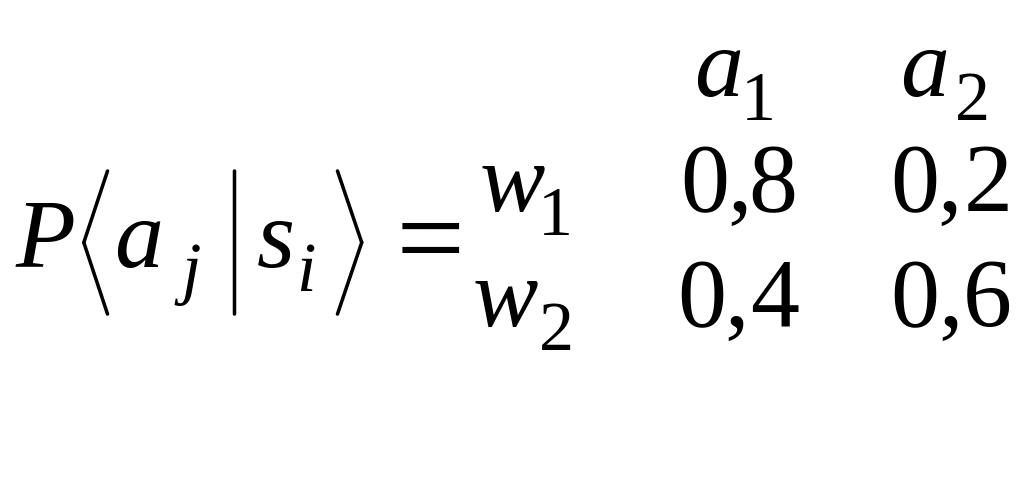
Здесь v₁, v₂ обозначают соответственно «успех» и «неудача», а w₁ и w₂ - «восприимчивый» и «невосприимчивый» покупатель.

Постройте новое дерево решений и определите оптимальный план действий фирмы.

54. Фирма планирует открыть новое предприятие в Арканзасе. В настоящее время имеется возможность построить либо крупное предприятие, либо небольшое, которое через 2 года можно будет расширить при условии высокого спроса на выпускаемую им продукцию. Рассматривается задача принятия решений на десятилетний период. Фирма оценивает вероятность сохранения высокого спроса на продукцию в течение 10 лет в 0,75. Стоимость немедленного строительства крупного предприятия составит 5 миллионов долларов, а небольшого – 1 миллион долларов. Расширение малого предприятия через 2 года обойдется фирме в 4,2 миллиона долларов. Прибыль, получаемая от функционирования производства на протяжении 10 лет – в следующей таблице.

Альтернативы	Ожидаемый доход (тысячи долларов)
	Высокий спрос	Низкий спрос
Крупное предприятие сейчас	1000	300
Небольшое предприятие сейчас	250	200
Расширенное предприятие через 2 года	900	200

1. Постройте соответствующее дерево решений, принимая во внимание, что через два года фирма может либо расширить небольшое предприятие, либо не расширять его.

2. Сформулируйте стратегию строительства для фирмы на планируемый 10-летний период (для простоты не принимайте во внимание возможную инфляцию).

55. Допустим, вы являетесь автором романа, который обещает быть популярным. У вас имеется возможность либо самостоятельно напечатать роман, либо через издательство. Издательство предлагает вам 20000 долларов за подписание контракта. Если роман будет пользоваться спросом, будет продано 200000 экземпляров, в противном случае – лишь 10000 экземпляров. Издательство выплачивает авторский гонорар в сумме один доллар за экземпляр. Исследование рынка, проведенное издательством, свидетельствует о том, что роман будет популярным. Если же вы сами напечатаете роман, то понесете потери в сумме 90000 долларов, связанные с печатанием и маркетингом, но в этом случае каждый проданный экземпляр принесет вам прибыль в два доллара.

1. Принимая во внимание имеющуюся информацию, примете ли вы предложение издательства или будете печатать роман самостоятельно?

2. Предположим, что вы заключили договор с литературным агентом на исследование, связанное с потенциальным успехом романа. Исходя из предыдущего опыта, компания извещает вас, что, если роман будет пользоваться спросом, исследование предскажет неверный результат в 20% случаев. Если же роман будет не популярен, то исследование предскажет верный результат в 85% случаев. Как эта информация повлияет на ваше решение?

56. Фермер Мак-Кой может выращивать либо кукурузу, либо соевые бобы. Вероятность того, что цены на будущий урожай этих культур повысятся, останутся на том же уровне или понизятся, равны соответственно 0,25, 0,30 и 0,45. Если цены возрастут, урожай кукурузы даст 30000 долларов чистого дохода, а урожай соевых бобов – 10000 долларов. Если цены останутся неизменными, Мак-Кой лишь покроет расходы. Но если цены станут ниже, урожай кукурузы и соевых бобов приведет к потерям в 35000 и 5000 долларов соответственно.

1. Представьте данную задачу в виде дерева решений.

2. Какую культуру следует выращивать Мак-Кою?

3. Ф ермер имеет дополнительный выбор, связанный с использованием земли как пастбища, что гарантированно принесет ему прибыль в 7500 долларов. Он получил также дополнительную информацию от брокера, касающуюся степени стабильности будущих цен на продукцию. Оценки брокера «благоприятный – неблагоприятный» затем выражаются количественно в виде следующих условных вероятностей:

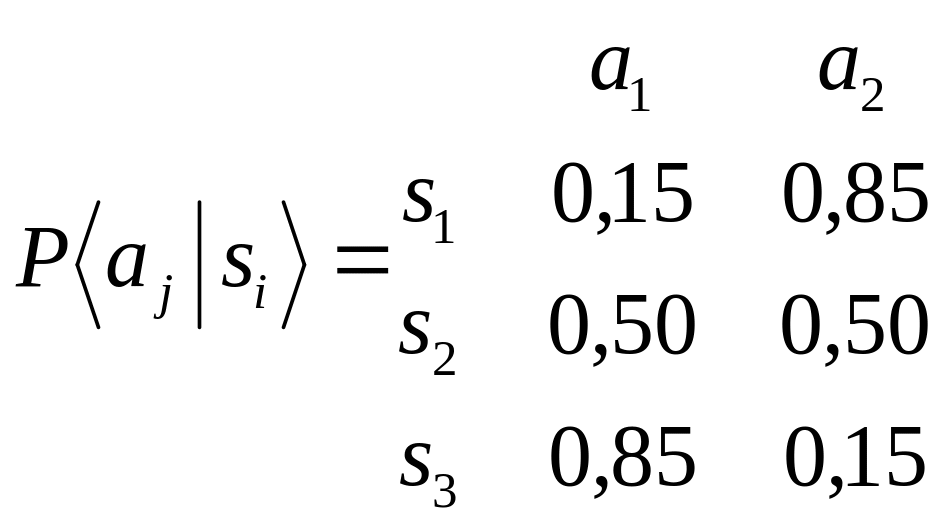
В данном случае а₁ и а₂ – оценки брокера «благоприятный» и «неблагоприятный», а s₁, s₂, s₃ представляют изменения в будущих ценах: соответственно «понижение», «такие же», «повышение». Постройте новое дерево решений и найдите оптимальное решение задачи.

57. Руководство некоторой компании решает, создавать ли для выпуска новой продукции крупное производство, малое предприятие или продать патент другой фирме. Размер выигрыша, который компания может получить, зависит от благоприятного или неблагоприятного состояния рынка (см. табл.).

Страте-гии	Действия компании	Выигрыш, долл., при состоянии экономической среды*
		благоприятном	неблагоприятном
1	Строительство крупного предприятия (А1)	200000	-180000
2	Строительство малого предприятия (А2)	100000	-20000
3	Продажа патента (А3)	10000	10000
* Вероятность благоприятного и неблагоприятного состояний экономической среды равна 0,5

1. Постройте дерево решений и найдите оптимальное решение.

2. Перед тем, как принимать решение о строительстве, руководство компании должно

определить, заказывать ли дополнительное исследование состояния рынка или нет, причем предоставляемая услуга обойдется компании в 10000 дол. Руководство понимает, что дополнительное исследование по-прежнему не способно дать точной информации, но оно поможет уточнить ожидаемые оценки конъюнктуры рынка, изменив тем самым значение вероятностей.

Предположим, что фирма, которой заказали прогноз, утверждает:

• ситуация будет благоприятной с вероятностью 0,45;

• ситуация будет неблагоприятной с вероятностью 0,55.

Известно, что когда фирма, исследующая состояние рынка, утверждает, что рынок благоприятный, то с вероятностью 0,78 этот прогноз оправдывается (с вероятностью 0,22 могут возникнуть неблагоприятные условия), прогноз о неблагоприятности рынка оправдывается с вероятностью 0,73. Постройте новое дерево решений и определите, как следует поступить руководству компании.

58. Директор лицея, обучение в котором осуществляется на платной основе, решает, следует ли расширять здание лицея на 250 мест, на 50 мест или не проводить строительных работ вообще. Если население небольшого города, в котором организован платный лицей, будет расти, то большая реконструкция могла бы принести прибыль в 250 тыс. руб. в год, незначительное расширение учебных помещений могло бы приносить 90 тыс. руб. прибыли. Если населе­ние города увеличиваться не будет, то крупное расширение обой­дется лицею в 120 тыс. руб. убытка, а малое - 45 тыс. руб. Однако информация о том, как будет изменяться население города, отсутст­вует. Постройте дерево решений и определите лучшую альтернати­ву, используя критерий Вальда. Чему равно значение ожидаемой денежной оценки) ОДО для наи­лучшей альтернативы при отсутствии необходимой информации?

Пусть при тех же исходных данных государственная статистиче­ская служба предоставила информацию об изменении численности населения: вероятность роста численности населения составляет 0,7; вероятность того, что численность населения останется неизменной или будет уменьшаться, равна 0,3. Определите наилучшее решение, используя критерий максимизации ожидаемой денежной оценки. Чему равно значение ОДО для наилучшей альтернативы при полу­чении дополнительной информации? Какова ожидаемая ценность дополнительной информации?

59. При крупном автомобильном магазине планируется открыть мастерскую по предпродажному обслуживанию и гарантий­ному ремонту автомобилей. Консультационная фирма готова пре­доставить дополнительную информацию о том, будет ли рынок благо­приятным или нет. Эти сведения обойдутся магазину в 13 тыс. руб. Администрация магазина считает, что эта информация гарантирует благоприятный рынок с вероятностью 0,5. Если рынок будет благо­приятным, то большая мастерская принесет прибыль в 60 тыс. руб., а маленькая – в 30 тыс. руб. При неблагоприятном рынке магазин потеряет 65 тыс. руб., если будет открыта большая мастерская, и 30 тыс. руб. если откроется маленькая. Не имея дополнительной информации, директор оценивает вероятность благоприятного рынка как 0,6. Положительный результат обследования гарантирует благоприятный рынок с вероятностью 0,8. При отрицательном результате рынок может оказаться благоприятным с вероятностью 0,3. Постройте дерево решений и определите:

• Следует ли заказать консультационной фирме дополнительную информацию, уточняющую конъюнктуру рынка?

• Какую мастерскую следует открыть при магазине: большую или маленькую?

• Какова ожидаемая денежная оценка наилучшего решения?

• Какова ожидаемая ценность дополнительной информации?

60. Фирма, производящая вычислительную технику, провела анализ рынка нового высокопроизводительного персональ­ного компьютера. Если будет выпущена крупная партия компьютеров, то при благоприятном рынке прибыль составит 250 тыс. руб., а при неблагоприятных условиях фирма понесет убытки в 185 тыс. руб. Небольшая партия техники в случае ее успешной реализации при­несет фирме 50 тыс. руб. прибыли и 10 тыс. руб. убытков при неблагоприятных внешних условиях. Возможность благоприят­ного и неблагоприятного исходов фирма оценивает одинаково. Исследование рынка, которое провел эксперт, обошлось фирме в 15 тыс. руб. Эксперт считает, что с вероятностью 0,6 рынок окажет­ся благоприятным. В то же время при положительном заключении благоприятные условия ожидаются лишь с вероятностью 0,8. При отрицательном заключении с вероятностью 0,15 рынок также может оказаться благоприятным. Используйте дерево решений, для того чтобы помочь фирме выбрать правильную технико-экономическую стратегию. Ответьте на следующие вопросы:

• Следует ли заказывать эксперту дополнительное обследование рынка?

• Какую максимальную сумму фирма может выплатить эксперту за проделанную работу?

• Какова ожидаемая денежная оценка наилучшего решения?

61. Павел Спицын провел анализ, связанный с откры­тием магазина велосипедов. Если он откроет большой магазин, то при благоприятном рынке получит 60 млн руб., при неблагопри­ятном — понесет убытки 40 млн руб. Маленький магазин принесет ему 30 млн руб. прибыли при благоприятном рынке и 10 млн руб. убытков — при неблагоприятном. Возможность бла­гоприятного и неблагоприятного рынка он оценивает одинаково. Исследование рынка, которое может провести профессор, обой­дется Спицыну в 5 млн руб. Профессор считает, что с вероятнос­тью 0,6 результат исследования рынка окажется благоприятным. В то же время при положительном заключении рынок окажется благоприятным с вероятностью 0,9. При отрицательном заключе­нии рынок может оказаться благоприятным с вероятностью 0,12,

Используйте дерево решений для того, чтобы помочь Павлу сделать правильный выбор. Следует ли заказать проведение обследования рынка? Следует ли открыть большой магазин? Какова ожидаемая стоимостная оценка наилучшего ре­шения?

62. Ивану Хлоркину, главному инженеру компании «Бе­лый каучук», надо решить, монтировать или нет новую производ­ственную линию с использованием последних технологий. Если новая линия будет работать безотказно, компания получит при­быль 200 млн. руб. Если линия откажет, компания может потерять 150 млн. руб. По оценкам Хлоркина, в 60% случаев новая линия откажет. Можно создать экспериментальную установку, а затем уже решать, монтировать или нет новую линию. Эксперимент обойдется в 10 млн руб. Иван считает, что в 50% случаев экспе­риментальная установка будет работать. Если она будет работать, то в 90% случаев производственная линия (если ее смонтировать) также будет работать. Если установка не будет работать, то есть только 20% шансов, что линия будет работать.

Следует ли строить экспериментальную установку?

Следует ли монтировать производственную линию?

Какова ожидаемая стоимостная оценка наилучшего решения?

63. Небольшая частная фирма производит косметиче­скую продукцию для подростков. В течение месяца реализуется 15, 16 или 17 упаковок товара. От продажи каждой упаковки фирма по­лучает 75 руб. прибыли. Косметика имеет малый срок годности, по­этому, если упаковка не продана в месячный срок, она должна быть уничтожена. Поскольку производство одной упаковки обходится в 115 руб., потери фирмы составляют 115 руб., если упаковка не про­дана к концу месяца. Вероятности продать 15, 16 или 17 упаковок за месяц составляют соответственно 0,55; 0,1 и 0,35. Сколько упаковок косметики следует производить фирме ежемесячно? Какова ожи­даемая стоимостная ценность этого решения? Сколько упаковок можно было бы производить при значительном продлении срока хранения косметической продукции?

64. Магазин «Молоко» продает в розницу молочные продукты. Директор магазина должен определить, сколько бидонов сметаны следует закупить у производителя для торговли в течение недели. Вероятности того, что спрос на сметану в течение недели будет 7, 8, 9 или 10 бидонов, равны соответственно 0,2; 0,2; 0,5 и 0,1. Покупка одного бидона сметаны обходится магазину в 70 руб., а продается сметана по цене 110 руб. за бидон. Если сметана не про­дается в течение недели, она портится и магазин несет убытки. Сколько бидонов сметаны желательно приобретать для продажи? Какова ожидаемая стоимостная ценность этого решения?

65. Найти наилучшие стратегии по критериям: макси-макса, Вальда, Сэвиджа, Гурвица (коэффициент пессимизма равен 0,2), Гурвица применительно к матрице рисков (коэффициент пессимиз­ма равен 0,4) для следующей платежной матрицы игры с природой (элементы матрицы - выигрыши):

66. Лукерья Скальпель — администратор больницы в Почаеве. Она решает, следует ли сделать к больнице большую при­стройку, маленькую пристройку или не делать пристройки вооб­ще. Если население Почаева будет продолжать расти, то большая пристройка могла бы приносить ежегодно прибыль в 150 тыс. руб. Если будет сделана маленькая пристройка, то она может прино­сить больнице 60 тыс. руб. прибыли ежегодно при условии, что население будет увеличиваться. Если население Почаева не будет увеличиваться, то сооружение большой пристройки принесет больнице убыток в 85 тыс. руб., а маленькой — в 45 тыс. руб. К со­жалению, у Лукерьи нет информации о том, как будет изменять­ся численность населения Почаева. Постройте таблицу решений. Определите наилучшую альтер­нативу, используя критерий безразличия.

1. Чему равно значение ЕМV для наилучшей альтернативы?

2. Получена дополнительная информация: вероятность роста населения равна 0,6, вероятность того, что его численность останется неизменной, — 0,4. Определите наилучшее реше­ние, используя критерий максимизации ожидаемой стоимост­ной оценки. Чему равно значение ЕМV для наилучшей альтернативы при наличии дополнительной информации?

3. Какова ожидаемая ценность дополнительной информации?

67. Тамара Пончик предполагает построить ресторан не­далеко от университетского общежития. Один из возможных ва­риантов — предусмотреть в нем пивной бар. Другой вариант не связан с продажей пива. В обоих случаях Тамара оценивает свои шансы на успех как 0,6 и на неудачу как 0,4. Предварительные обсуждения показывают, что план, связанный с продажей пива, может принести 325 тыс. руб. прибыли. Без продажи пива можно заработать 250 тыс. руб. Потери в случае открытия ресторана с ба­ром составят 70 тыс. руб., в случае ресторана без бара — 20 тыс. руб. Выберите альтернативу для Тамары Пончик на основе средней стоимостной оценки в качестве критерия.

1. Следует ли реализовать план, предусматривающий продажу пива?

2. Чему равно значение ЕМV наилучшей альтернативы?

68. «Фотоколор» — небольшой магазин, торгующий хи­мическими реактивами, которые используются некоторыми фо­тостудиями при обработке пленки. Один из продуктов, который предлагает «Фотоколор», — фиксаж ВС-6. Адам Полутонов, ди­ректор магазина, продает в течение месяца 11, 12 или 13 ящиков ВС-6. От продажи каждого ящика фирма получает 35 тыс. руб. прибыли. Фиксаж ВС-6, как и многие фотореактивы, имеет ма­лый срок годности. Поэтому, если ящик не продан к концу меся­ца, Адам должен его уничтожить. Так как каждый ящик обходит­ся магазину в 56 тыс. руб., он теряет их в случае, если ящик не продан к концу месяца. Вероятность продать 11, 12 или 13 ящи­ков в течение месяца равна соответственно 0,45; 0,35 и 0,2. 1.

Сколько ящиков закупать фирме для продажи ежемесячно? Какова ожидаемая стоимостная оценка этого решения? Сколько ящиков следовало бы закупать, если бы Адам мог достать фиксаж ВС-6 с добавкой, которая значительно про­длевает срок его годности?

69. Компания «Молодой сыр» — небольшой производи­тель различных продуктов из сыра. Один из продуктов — сырная паста — продается в розницу. Вадим Ароматов, менеджер компа­нии, должен решить, сколько ящиков сырной пасты следует про­изводить в течение месяца. Вероятность того, что спрос на сыр­ную пасту в течение месяца будет 6, 7, 8 или 9 ящиков, равна со­ответственно 0,1; 0,3; 0,5; 0,1. Затраты на производство одного ящика пасты составляют 45 тыс. руб. Ароматов продает каждый ящик по цене 95 тыс. руб. Если сырная паста не продается в те­чение месяца, то она портится и компания не получает дохода.

Сколько ящиков следует производить в течение месяца? Какова ожидаемая стоимостная оценка этого решения?

70. Дмитрий Мухин не знает, что ему предпринять. Он может открыть в своей аптеке или большую, или маленькую сек­цию проката видеокассет. Мухин может получить дополнитель­ную информацию о том, будет рынок видеопроката благоприят­ным или нет. Эта информация обойдется ему в 3 млн. руб. Дмит­рий считает, что эта информация окажется благоприятной с вероятностью 0,5. Если рынок будет благоприятным, то большая секция проката принесет прибыль 15 млн. руб., а маленькая — 5 млн. руб. При неблагоприятном рынке Мухин потеряет 20 млн. руб. в случае, если он откроет большую секцию, и 10 млн. руб. в случае, если маленькую. Не имея дополнительной информации, Дмитрий оценивает вероятность благоприятного рынка как 0,7. Положи­тельный результат обследования гарантирует благоприятный ры­нок с вероятностью 0,9. При отрицательном результате рынок может оказаться благоприятным с вероятностью 0,4.

Следует ли получить дополнительную информацию?

Следует ли открыть большую секцию?

Какова ожидаемая стоимостная оценка наилучшего решения?

71. Диспетчер автобусного парка (ЛПР) в летние месяцы в конце каждой недели должен принять решение о целесообразности выделения дополнительных автобусов на загородный маршрут. ЛПР имеет три варианта решений: увеличить количество автобусов на 10 (стратегия А1), увеличить это количество на 5 (стратегия А2) или оставить без изменения обычное число автобусов на линии (стратегия А3). Возможны два состояния погоды: В1 – плохая погода, В2 – хорошая погода, причем в момент принятия решения нет возможности определить ожидаемое состояние погоды. Если в выходные дни будет хорошая погода и много желающих выехать за город, а выделено мало автобусов, то парк понесет убытки, связанные с недополученной прибылью. Если же выделены дополнительные автобусы, а погода окажется плохой, то возникнут потери вследствие эксплуатации незаполненных автобусов.

Пусть на основе анализа статистических данных за определенный период установлена функция потерь для возможных комбинаций состояний природы и решений ЛПР в виде матрицы игры, в которой отрицательные значения показывают дополнительную прибыль, а положительные – потери:

Используя критерии Вальда, Сэвиджа, Гурвица, выберите оптимальную стратегию ЛПР.

72. Швейное предприятие, выпускающее детские платья и костюмы, реализует свою продукцию через фирменный магазин. Сбыт продукции зависти от состояния погоды. По данным прошлых наблюдений предприятие в течение апреля – мая в условиях теплой погоды может реализовать 600 костюмов и 1975 платьев, а при прохладной погоде – 1000 костюмов и 625 платьев. Известно, что затраты на единицу продукции в течение указанных месяцев составили для костюмов 27 руб., для платьев 8 руб., а цена реализации равна соответственно 48 руб. и 16 руб.

Определить оптимальную стратегию предприятия, обеспечивающую при любой погоде определенный средний доход. Решить задачу методами теории игр.

73. Пекарня печет хлеб на продажу магазинам. Стоимость 1 булки составляет 30 пенсов, ее продают за 40 пенсов. В таблице приведены данные за последние 50 дней.

Спрос в день, тыс. шт.	10	12	14	16	18
Число дней	5	10	15	15	5

Если булка испечена, но не продана, то убытки составят 20 пенсов за штуку. Используйте критерии Сэвиджа, Вальда Гурвица и Байеса для принятия решения о количестве выпекаемого хлеба.

74. Руководство фирмы пытается уладить с профсоюзом вопрос о забастовке, которая может принести фирме убытки в размере 6 млн.руб. в неделю. Профсоюз требует увеличения заработной платы на 20%, что приведет к потерям фирмы на фонде зарплаты в размере 20 млн.руб. Если увеличить зарплату на 10%, то потери фирмы на фонде зарплаты составят 10 млн.руб., но при этом возникнет 20%-ный риск возникновения забастовки продолжительностью в одну неделю. Если повысить зарплату всего на 5%, то потери фирмы на фонде зарплаты снизятся до 5 млн.руб., но вероятность возникновения забастовки повысится до 60% , а ее продолжительность в таком случае может составить 2 недели. Наконец, если полностью отказать профсоюзу в повышении зарплаты, то риск возникновения забастовки вырастет до 90%, а ее продолжительность может достигнуть 4 недель. Что из вышеперечисленного является для фирмы оптимальным решением ?

75. Информация о возможном заработке в четырех местах будущей работы (государственное учреждение, частная фирма, коммерческий банк и страховая компания) представлена в следующей таблице выплат.

Таблица. Ожидаемый месячный заработок ( в тыс.руб.)

___________________________________________________________

Состояния хозяйственной конъюнктуры

и их вероятности

_____________________________________

Выбор Хорошее ( 0.7 ) Плохое ( 0.3 )

___________________________________________________________

Госучреждение 500 500

Фирма 900 100

Банк 700 300

Страховая компания 200 900

Какой выбор будущего места работы здесь надо считать оптимальным? Как он изменится, если вероятность хорошего состояния конъюнктуры составит 0.3, а плохого - 0.7?

Сделайте выбор будущего места работы с помощью критерия Лапласа и Гурвица. Показатель степени оптимизма в последнем случае возьмите по своему усмотрению в соответствии со своей оценкой перспектив развития экономики страны.

76. Имеется 3 типа дробильного оборудования и 2 вида отходов. Удельные затраты на дробление 1 т отходов в зависимости от применяемого оборудования – в таблице. Применив игровой подход, определите состав оборудования.

Виды отходов	Типы оборудования
	Д1	Д2	Д3
1	23	22	26
2	35	42	17

77. В зависимости от изменений рыночной конъюнктуры фирма должна решить вопрос об изменении объема производства своей продукции: увеличить его при улучшении конъюнктуры и сократить при ухудшении. Непринятие мер и выбор неверного решения грозит убытками или в лучшем случае - упущенной прибылью. Информация о возможных последствиях (об изменении суммы прибыли) от принятия того или иного варианта решения в условиях той или иной конъюнктуры приведена ниже в таблице выплат. Выберите оптимальный вариант решения в предположении, что вероятность улучшения конъюнктуры равна 0.1, а ухудшения - 0.6.

Ожидаемые выплаты (млн.руб.)

+--------------------------------------------------+

¦Вариант решения ¦ Изменение конъюнктуры ¦

¦об изменении +---------------------------------¦

¦объема про -ва ¦улучшится ¦не изменится¦ухудшится¦

+----------------+----------+------------+---------¦

¦1.Увеличить ¦ + 100 ¦ - 20 ¦ - 50 ¦

+----------------+----------+------------+---------¦

¦2.Не менять ¦ + 20 ¦ 0 ¦ - 20 ¦

+----------------+----------+------------+---------¦

¦3.Сократить ¦ + 10 ¦ - 10 ¦ - 10 ¦

+--------------------------------------------------+

Как изменится выбор оптимального решения, если упомянутые вероятности станут равны соответственно 0.3 и 0.3 ?

78. В зависимости от изменений рыночной конъюнктуры фирма должна решить вопрос об изменении объема производства своей продукции: увеличить его при улучшении конъюнктуры и сократить при ухудшении. Непринятие мер и выбор неверного решения грозит убытками или в лучшем случае - упущенной прибылью. Информация о возможных последствиях (об изменении суммы прибыли) от принятия того или иного варианта решения в условиях той или иной конъюнктуры приведена ниже в таблице выплат. Выберите оптимальный вариант решения в предположении, что вероятность улучшения конъюнктуры равна 0.7, а ухудшения - 0.1. Используйте также для оптимального выбора критерии Лапласа и Гурвица. При использовании критерия Гурвица показатель степени оптимизма возьмите в соответствии с Вашей оценкой перспектив развития экономики страны на ближайшее будущее.

Ожидаемые выплаты (млн.руб.)

+--------------------------------------------------+

¦Вариант решения ¦ Изменение конъюнктуры ¦

¦об изменении +---------------------------------¦

¦объема про -ва улучшится не изменится ¦ухудшится¦

+----------------+----------+------------+---------¦

¦1.Увеличить ¦ + 200 ¦ - 50 ¦ - 150 ¦

+----------------+----------+------------+---------¦

¦2.Не менять ¦ 0 ¦ 0 ¦ - 20 ¦

+----------------+----------+------------+---------¦

¦3.Сократить ¦ - 5 ¦ - 5 ¦ - 5 ¦

+--------------------------------------------------+

79. Банк заинтересован в покупке акций некоего акционерного общества. Стремясь сделать покупку как можно более выгодной, банк снабжает продавца информацией о реальной стоимости акций, которая может быть как правдивой (А₁), так и заведомо ложной (А₂). Продавец может как поверить информации (В₁), так и не поверить (В₂).

Условия задачи можно представить в виде игровой ситуации, платежная матрица которой имеет вид:

Банк	Продавец акций
	В1	В2
А1	0,608	1
А2	1	0,44

Необходимо выбрать такую стратегию банка, при которой результат окажется максимально возможным.

СТОХАСТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

80. Предприятие производит продукцию двух видов в количестве х₁ и х₂. Исходные данные – в таблице 1.

Таблица 1.

Ресурсы	Расход ресурсов на единицу продукта вида		Производственная мощность
	1	2
I	а11	а12	120
II	а21	а22	2600
Прибыль	1,2	2,8

Величины а_ij случайные, их распределение представлено (возможные значения и вероятности) в табл. 2.

Таблица 2.

Значение	Вероятность	Значение	Вероятность

Определить оптимальный план производства продукции по критерию максимум прибыли.

81. Рассмотрите задачу о распределении двух видов ресурсов для выпуска двух типов продукции, используя данные табл. 1.

Таблица 1.

Величина		Ограничения	Случайные величины
х1	2	1	1	0,305	4	0,305	5	0,61
х2	3	2	2	0,305	1	0,305	10	0,61

Здесь с_j и являются случайными величинами и обозначают соответственно прибыль на единицу продукции, нормы расхода ресурсов и запас ресурсов; и – дисперсии и ; , , – математические ожидания величин с_j и соответственно.

Контрольная работа включает 3 расчетных задания.

1. Моделирование конкретной производственной ситуации, выбор метода, решение задачи, анализ результатов с использованием оптимальных оценок, постоптимальный анализ, выработка рекомендаций по повышению эффективности производства на основе выполненного анализа.

2. Решение экономических задач на основе использования методов нелинейного и стохастического программирования.

3. Использование игровых моделей и статистических критериев в принятии решений.

Разобравшись в сущности исследуемой проблемы, студент должен подготовить необходимую информацию для проведения расчетов, которые предполагается выполнить с помощью персонального компьютера.

После выполнения расчетов, необходимо сделать выводы и, оформив контрольную работу в соответствии с общими требованиями, сдать ее на проверку, подписав и указав использованные литературные источники.

Список литературы

1. М.Ю. Афанасьев, Б.П. Суворов. Исследование операций в экономике. – М.: Инфра – М, 2003. – 444 с.

2. В.А.Бункин, Б.Я.Курицкий, Ю.А.Сокуренко. Решение задач оптимизации в управлении машиностроительным производством. – Л.: Машиностроение, 1976. – 232 с.

3. Г. Вагнер. Основы исследования операций. В 3 т. – М.: Мир, 1972.

4. А.А.Горчаков, И.В.Орлова. Компьютерные экономико-математические модели. – М.: Компьютер, 1995. – 134 с.

5. О.О.Замков, А.В.Толстопятенко, Ю.Н.Черемных. Математические методы в экономике. – М.: МГУ: , 1997. - 364 с.

6. О.А. Косоруков, А.В, Мищенко. Исследование операций. – М.: «Экзамен», 2003. – 448 с.

7. А.В. Крушевский, К.И.Швецов. Математическое программирование и моделирование в экономике. – К., 1979. - 454 с.

8. А.В. Крушевский. Теория игр. – К.: Вища школа, 1977. – 214 с.

9. Б. Кузин, В. Юрьев, Г. Шахдинаров. Методы и модели управления фирмой. – СПб: Питер, 2001. – 432 с.

10. А.В. Кузнецов, В.А. Сакович, Н.И. Холод. Математическое программирование. – Мн.: Выш. школа, 1994. – 285 с.

11. Б.Я. Курицкий. Поиск оптимальных решений средствами Excel 7.0. - СПб: ВНV, 1997. – 384 с.

12. Б.Я. Курицкий. Оптимизация вокруг нас. – Л.: Машиностроение, 19897. – 145 с.

13. И.В. Орлов. Экономико-математическое моделирование. – М.: Вузовский учебник, 2005. – 144 с.

14. Х.А. Таха. Введение в исследование операций. – М., СПб., К.: «Вильямс», 2001. – 911 с.

15. С.Р. Хачатрян, М.В. Пинегина, В.ПБуянв. Методы и модели решения экономических задач. – М.: «Экзамен», 2005. – 384 с.

16. Т.Дж Уотшем, К. Паррамоу. Количественные методы в финансах. – М.: Финансы, 1999. – 527 с.

17. М. Эддоус, Р.Стэнфилд. Методы принятия решений. – М.: «Аудит», 1997. – 589 с.

18. Экономико-математические методы и модели / Н.И. Холод, А.В. Кузнецов и др. – Мн.: БГЭУ, 1999. – 413 с.

19. Ястремский А.И. Стохастические модели математической экономики. – К., 1983.

1 Учебно-методическое пособие по изучению «Математического программирования», с.92