4. Назначение целевой функции

Для вычисления значений целевой функции, соответствующей минимальным суммарным затратам на доставку песка, необходимо зарезервировать ячейку и ввести формулу для ее вычисления

.

Для этого

• поместим курсор в ячейку В19 (после решения задачи здесь будет находиться величина целевой функции);

• войти в Мастер функций, категория Математические, функция СУММАПРОИЗВ;

• в окне СУММАПРОИЗВ в поле Массив 1 указать адрес массива В12 : Е17 (удельные затраты на доставку груза) и в поле Массив 2 – В3 : Е8 (объемов поставок);

• нажать кнопку ОК – подтверждение окончания ввода адресов массивов.

В ячейке В19 появится числовое значение, равное произведению единичных поставок на удельные коэффициенты затрат (в данной задаче – это число 256) (рис 1.9).

5. Ввод зависимостей из математической модели

Для этого необходимо выполнить следующие действия:

• выбрать Сервис => Поиск решения;

• поместить курсор в поле Установить целевую (ячейку);

• ввести адрес $В$19 (тем самым мы резервируем ячейку, куда после решения задачи помещается значение целевой функции) или поместить курсор в В19, а затем выбрать Поиск решения. При этом в поле адреса целевой ячейки будет автоматически введен адрес $В$19;

• установить направление изменения целевой функции, равное Минимальному значению;

• ввести адреса изменяемых ячеек ВЗ : Е8. Для этого необходимо:

  • выбрать Изменяя ячейки;

  • ввести адреса $В$3:$Е$8 или щелкнуть на красной стрелке рядом с этим полем, выйти в таблицу с матрицей перевозок, выделить блок ячеек ВЗ : Е8, щелкнуть на красной стрелке и вернуться в блок Поиск решения. Такая последовательность действий приводит к тому, что будут введены нужные адреса.

6. Ввод ограничений задачи.

1) В матрицу перевозок, содержащую исходные данные по зада­че, введем условие реализации мощностей всех по­ставщиков (рис. 1.10). Для этого необходимо:

• выбрать Добавить ограничения;

• в поле Ссылка на ячейку ввести адреса $A$3 : $A$8;

• в среднем поле установить знак « ». Для этого щелкнуть спинер и выбрать необходимый знак « »;

• в поле Ограничение установить адреса $А$12 : $А$17;

• для подтверждения введенного условия нажать кнопку ОК.

2) введем ограничение, которое реализует условие удов­летворения мощностей всех потребителей (рис. 1.10). Для этого необходимо:

• выбрать Добавить ограничения;

• в поле Ссылка на ячейку ввести адреса $В$9 : $Е$9;

• в поле знака выбрать при помощи спинера знак « = »;

• в поле Ограничение установить адреса $В$12 : $Е$12;

• нажать кнопку ОК;

• после этого надо вернуться в поле Поиск решения;

• после ввода всех ограничений ввести ОК. На экране появится окно Поиск решения с введенными ограничениями (рис. 1.10).

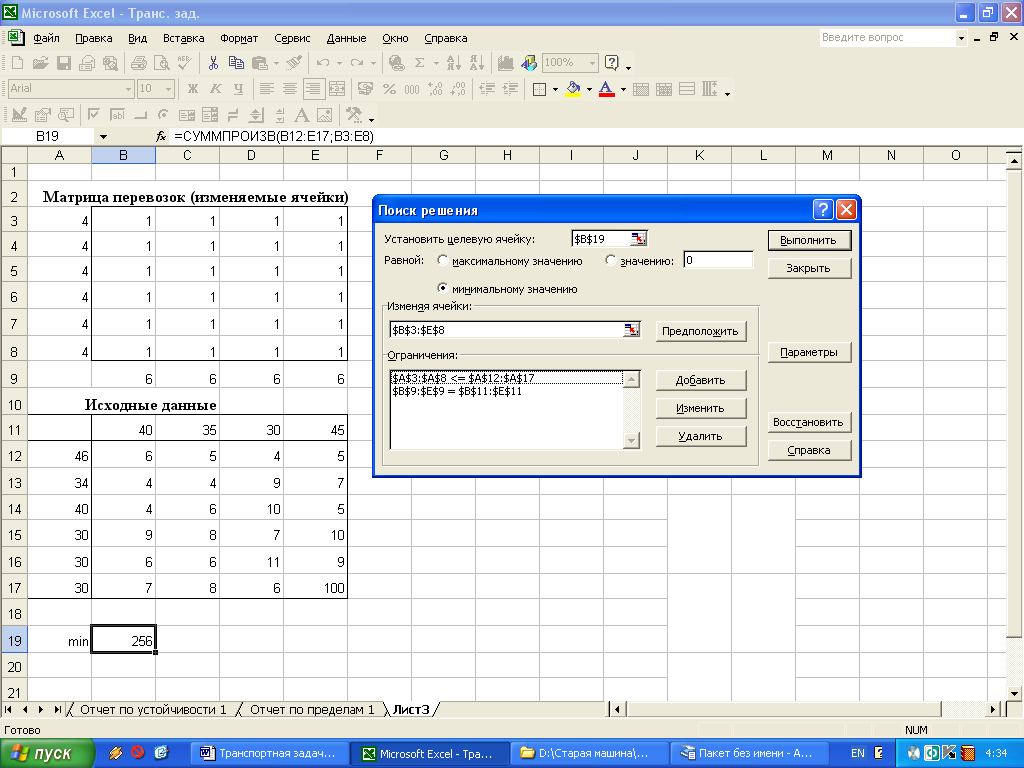
рис. 1.10

7. Ввод параметров.

С помощью окна Параметры введем условия для реше­ния оптимизационной задачи. Для этого необходимо:

• щелкнуть по кнопке Параметры;

• выбрать переключатель Линейная модель;

• выбрать переключатель Неотрицательные значения;

• нажать кнопку ОК. После этого произойдет переход в поле Поиск решения;

• нажать кнопку Выполнить. На экране появится диалоговое окно Результаты поиска решения (рис. 1.11).

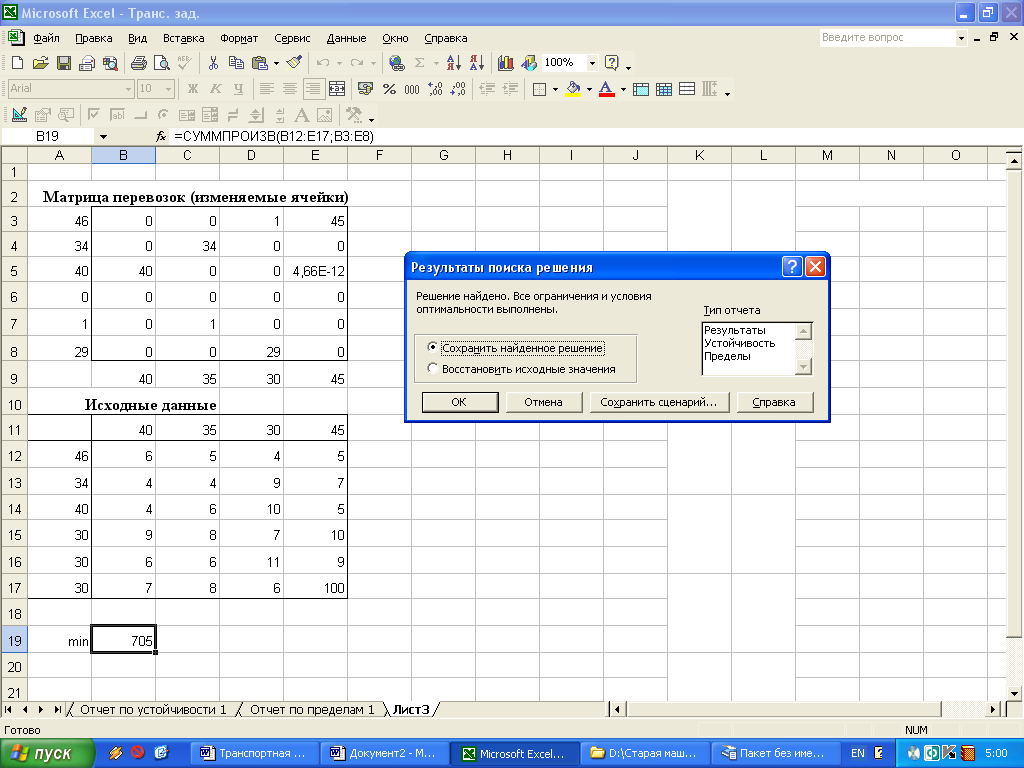
Рис. 1.11

В результате получен оптимальный план перевозок (табл. 1.6), позволяющий удовлетворить спрос всех строительных площадок в песке с минимальными суммарными затратами, равными 705 ден. ед.

Таблица 1.6 – Оптимальный план перевозки песка

	40	35	30		45
46	0	0		1	45
34	0	34		0	0
40	40	0		0	0
0	0	0		0	0
1	0	1		0	0
29	0	0		29	0

Следует отметить, что этот план отличается от решения, найденного ранее и помещенного в табл. 2.23¹, и представляет один из множества оптимальных планов, которые характеризуются минимальными затратами в 705 ден. ед.

В соответствии с полученным решением (табл. 1.6) принимаются 2-й вариант расширения добычи песка (причем на втором карьере мощность следует увеличить только на 1 т песка в день) и 3-й (открыть новый карьер мощностью 29 т/день).

Такой план можно получить из решения, полученного ранее и представленного здесь в таблице 1.7, если к клетке с нулевой характеристикой A₄ В₃ построить цикл (табл. 1.7) и по этому циклу перемещать поставку в размере min {30, 30, 30, 29, 29} = 29. Полученное таким образом новое решение представлено в табл. 1.8.

Таблица 1.7.

Мощность поставщиков		В1	В2	B3	В4	Bф
		40	35	30	4 5	60
A1	46	6	5	4 – 30	5 + 16	0
A2	34	4 – 29	4 + 5	9	7	0
A3	40	4 + 11	6	10	5 – 29	0
A1	30	9	8	7	10	0 30
A2	30	6 + 0	6 – 30	11	9	0 + 0
A4	30	7	8	6 + 0	М	0 – 30

Таблица 1.8.

Мощность поставщиков		В1	В2	B3	В4	Bф
		40	35	30	4 5	60
A1	46	6	5	4 1	5 45	0
A2	34	4 0	4 34	9	7	0
A3	40	4 40	6	10	5	0
A1	30	9	8	7	10	0 30
A2	30	6 0	6 1	11	9	0 29
A4	30	7	8	6 29	М	0 1

Как видим, это решение совпадает с оптимальным планом, полученным с помощью Excel и представленным в табл. 1.6.