1.3 Решение транспортной задачи линейного программирования с помощью Excel

Для решения транспортной задачи в Excel используем программу Поиск решения, воспользовавшись исходными данными следующего примера.

Строительный песок добывается в трех карьерах и доставляется на четыре строительные площадки. Дан­ные о производительности карьеров за день (а_i в т), потребностях в песке строительных площадок (b_j в т), затратах на добычу песка (d_i; в ден. ед./т) и транспортных расходах (g_ij) приведены в таблице 1.4:

Таблица 1.4 – исходные данные

a i bj	40	35	30	45	di
46	4	3	2	5	2
34	1	1	6	4	3
40	3	5	9	4	1

Недостающее количество песка — 30 т в день можно обеспечить следующими тремя путями:

1) увеличение производительности 1-го карьера, что повлечет за собой дополнительные затраты в 3 ден. ед. на добычу 1 т.

2) увеличение производительности 2-го карьера с дополнительными затратами в 2 ден. ед. /т.

3) эксплуатация нового карьера с затратами на добычу 5 ден. ед./т и на транспортировку к указанным строи­тельным площадкам с₄₁ = 2, с₄₃ = 3 и с₄₃ = 1 (ден. ед./т).

Определить оптимальный план закрепления строи­тельных площадок за карьерами и оптимальный вариант расширения поставок песка.

Решение.

Сформируем матрицу производственно-транспортных затрат, в которую включим в качестве отдельных поставщиков и варианты расширения добычи песка (табл. 1.5).

Табл. 1.5.

Мощности поставщиков	Спрос потребителей
	40	35	30	45
46	6	5	4	5
34	4	4	9	7
40	4	6	10	5
30	9	8	7	10
30	6	6	11	9
30	7	8	6	100

Математическая модель задачи:

Целевая функция:

F = 6 х₁₁ + 5 х₁₂ + 4 х₁₃ + 5 х₁₄ + 4 х₂₁ + 4 х₂₂ + 9 х₂₃ + 7 х₂₄ +

+ 4 х₃₁ + 6 х₃₂ + 10 х₃₃ + 5 х₃₄ + 9 х₄₁ + 8 х₄₂ + 7 х₄₃ + 10 х₄₄ +

+ 6 х₅₁ + 6 х₅₂ + 11 х₅₃ + 9 х₅₄ + 7 х₆₁ + 8 х₆₂ + 6 х₆₃ + М х₆₄  min

Ограничения

1) по мощности поставщиков:

х₁₁ + х₁₂ + х₁₃ + х₁₄  46,

х₂₁ + х₂₂ + х₂₃ + х₂₄  34,

х₃₁ + х₃₂ + х₃₃ + х₃₄  40,

х₄₁ + х₄₂ + х₄₃ + х₄₄  30,

х₅₁ + х₅₂ + х₅₃ + х₅₄  30,

х₆₁ + х₆₂ + х₆₃ + х₆₄  30,

2. по спросу потребителей:

х₁₁ + х₂₁ + х₃₁ + х₄₁ + х₅₁ + х₆₁ = 40,

х₁₂ + х₂₂ + х₃₂ + х₄₂ + х₅₂ + х₆₂ = 35,

х₁₃ + х₂₃ + х₃₃ + х₄₃ + х₅₃ + х₆₃ = 30,

х₁₄ + х₂₄ + х₃₄ + х₄₄ + х₅₄ + х₆₄ = 45,

2. неотрицательности переменных:

Транспортная задача является открытой, т.к. предложение продукта и спрос на него не совпадают:

210 ≠ 150.

1. Создание формы для решения задачи – создание матрицы перевозок начинается с резервирования изменяемых ячеек. Для этого в блок ячеек В3:Е8 вводятся «1», так резервируется место, где после решения задачи будет находиться распределение поставок (рис. 1.9).

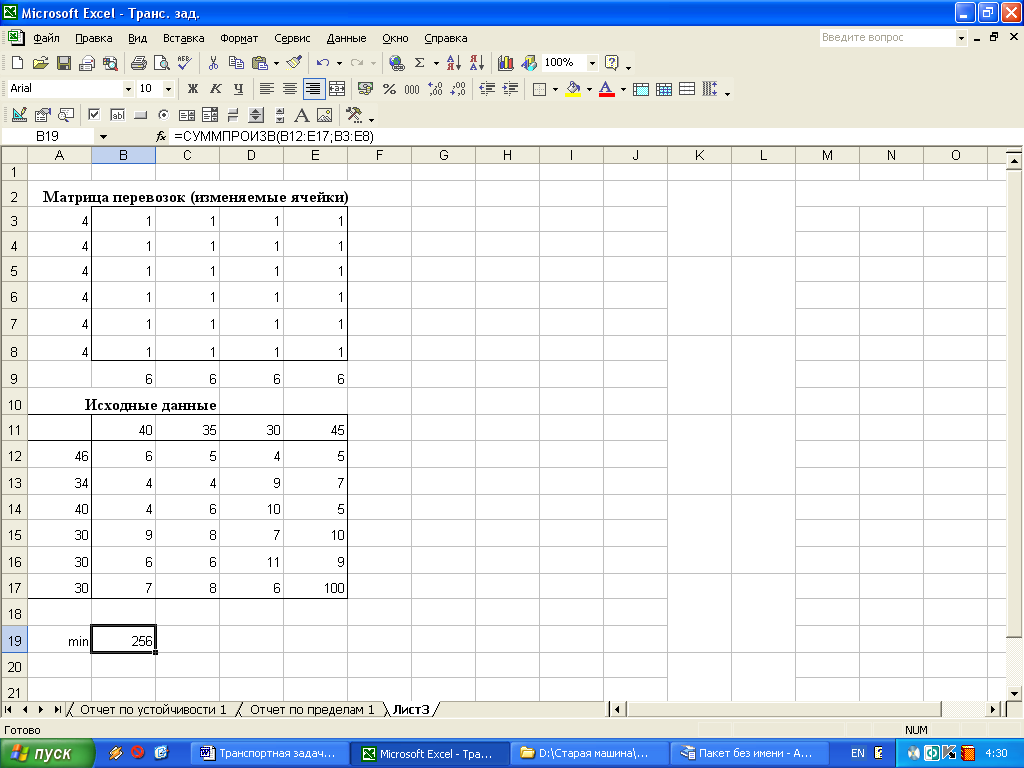
Рис. 1.9. Создание формы для ввода условий задачи.

2. Ввод исходных данных – ввод мощностей поставщиков (ячейки А12:А17), спроса потребителей (ячейки В11:Е11), а также удельные затраты по добыче и доставке песка по каждого поставщика потребителям (блок В12:Е17, причем здесь вместо М ввели превышающее другие затраты число 100) (рис. 1.9).

3. Ввод граничных условий (рис. 1.9)

1) ввод условий реализации продукта поставщиков

,

для чего необходимо выполнить следующие операции:

• поместить курсор в ячейку А3;

• выбрать знак ;

• выделить необходимые для суммирования ячейки В3:Е3;

• нажать ENTER для подтверждения ввода формулы для суммирования;

• скопировать формулу, помещенную в А3, протянув мышь через ячейки А3:А8.

2) ввод условий удовлетворения потребностей потребителей

,

для этого необходимо выполнить операции:

• поместить курсор в ячейку В9;

• выбрать знак , при этом автоматически выделяется весь столбец В3:В8;

• нажать ENTER для подтверждения суммирования элементов выделенного столбца;

• скопировать формулу, помещенную в В9, протянув мышь через ячейки В9:Е9.