О.В. Свеженцева

Разработка и тестирование генетического алгоритма оптимального размещения источников питания в распределительной электрической сети

Современные электроэнергетические системы (в том числе системы электроснабжения) являются сложными территориально протяженными системами, имеющими неоднородную структуру электрических сетей. Ввиду сложности и многомерности современных систем электроснабжения, многовариантности и многокритериальности, наличия различных предпочтений при выборе решений, проблема обоснования развития систем электроснабжения в виде общей задачи исследования операций является громоздкой и с практической точки зрения непреодолимой.

С учетом сложности проблемы, ее решение целесообразно рассматривать как систему задач, поэтапно уточняющих и детализирующих решения по развитию систем электроснабжения[1].

1. На первом уровне (этапе) решаются задачи оптимизации размещения источников питания (ИП), выбора в первом приближении рациональной конфигурации электрической сети. Конкретная реализация необходимых свойств электрической сети может быть получена различными способами, отличающимися величинами приведенных затрат, экономичностью. Обычно экономичность характеризуется стоимостными показателями – приведенными затратами. Наличие термина «различными способами» подразумевает рассмотрение оптимизационной задачи, поэтому задачи, возникающие при проектировании рациональной конфигурации электрической сети, относятся к различным постановкам задач оптимального выбора. При этом при нахождении минимума (максимума) целевой функции используются в общем случае произвольного вида ограничения.

Конфигурация электрической сети в общем случае однозначно определяет топологические свойства сети.

2. На втором уровне решаются следующие задачи: уточняются найденные решения с учетом требований по качеству электрической энергии и с учетом требований надежности к системам электроснабжения.

3. На третьем этапе проводят анализ функционирования сформированной системы электроснабжения путем расчетов различных режимов работы системы.

В целом задача выбора решений при построении рациональной конфигурации распределительной электрической сети включает в себя следующие подзадачи [2]:

1. оптимальное расположение подстанций;

2. оптимизация прокладки линий с учетом ограничений на местности;

3. оптимальное закрепление потребителей за подстанциями;

4. оптимальный выбор мощности подстанций;

5. выбор оптимального числа трансформаторов на подстанциях.

В данной статье рассматривается и решается одна задача первого уровня, а именно задача оптимального размещения нескольких источников питания одинакового типоразмера в распределительной электрической сети методами генетического программирования и одновременного закрепления потребителей за выбранными ИП.

Общая постановка задачи. Пусть в декартовой системе координат (на плоскости) задана система точек c координатами, , которые будем именовать в дальнейшем точками потребления электроэнергии. Множество множество пунктов потребления электроэнергии.

Каждому потребителю сопоставляется некоторый вес , равный потребляемой мощности этим потребителем. Множество однозначно определяет объемы потребления. Таким образом, задана также суммарная потребляемая мощность всеми потребителями в рассматриваемой задаче.

(1)

Пусть также в декартовой системе координат задана система точек

с координатами возможных мест размещения источников питания, где количество этих возможных мест; априори предполагается, что это число заведомо больше практически необходимого числа мест размещения ИП.

Зададим типовой ряд используемых для решения задачи источников электрической мощности (источников питания, генераторов). Здесь используем следующее соглашение: считаем, что источник питание сам производит электрическую энергию и условно считается в нашей задаче генератором. В данной постановке считаем, что мощности всех ИП одинаковы и равны . Очевидно, что для суммарной отдаваемой мощности должно выполняться следующее неравенство:

, (2)

С учетом всего вышеизложенного имеем следующую оптимизационную задачу: требуется выбрать наиболее экономичный вариант размещения ИП с учетом затрат на доставку электроэнергии к потребителям, причем следует выбрать оптимально следующие параметры:

• места размещения источников питания из предложенных возможных мест размещения;

• для каждого потребителя, определить за каким источником питания он будет закреплен.

Целевая функция (ЦФ), минимум которой будем находить, может быть представлена в виде:

.

(3)

Здесь предполагается, что функция затрат на передачу электроэнергии зависит от величины передаваемой мощности и от расстояний от источников питания до потребителей . удельные приведенные затраты для передачи единицы мощности на единицу расстояния. При этом принимаем допущение, что существующая электрическая сеть не ограничивает передачу мощности от ИП до потребителей.

Расстояние от ИП до потребителя может вычисляться по одной из двух возможных метрик:

1. -метрика Вебера;

2. - метрика Евклида,

где координаты пункта потребления,

координаты возможного пункта размещения ИП, ,

Будем в дальнейшем решать задачу в предположении, что имеем радиальную электрическую сети и что удельные приведенные затраты , т.е. ЦФ принимает вид:

.

(4)

В данной постановке задача может интерпретироваться как задача дискретной оптимизации. В классическом случае эту задачу решают с помощью методов комбинаторного анализа. В специальной литературе часто встречается понятие комбинаторной задачи или задачи комбинаторного поиска, однако трудно найти достаточно общее определение, которое покрывало бы все разнообразие задач такого рода. Рассмотрим комбинаторную задачу фиксированной размерности [3].

Даны конечных множеств (множества значений переменных) и множество значений параметров . Задана также функция ограничений , описывающая область допустимых значений переменных при значении параметра .

Требуется для заданных исходных данных построить и далее возможна одна из трех постановок задачи:

1. любой набор значений , такой, что 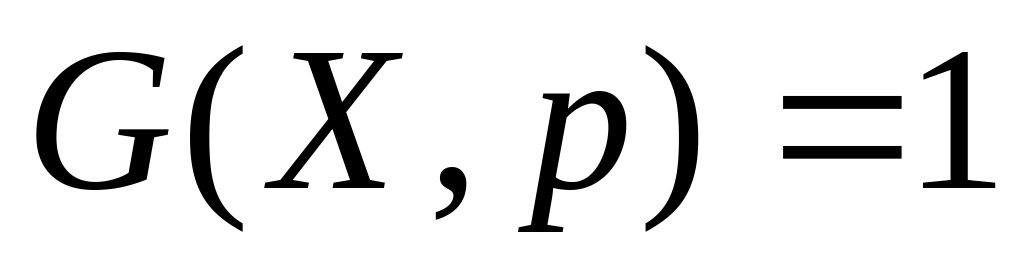(задача поиска);

2. все наборы значений , такие, что (задача перечисления);

3. такой набор значений , что и заданная целевая функция 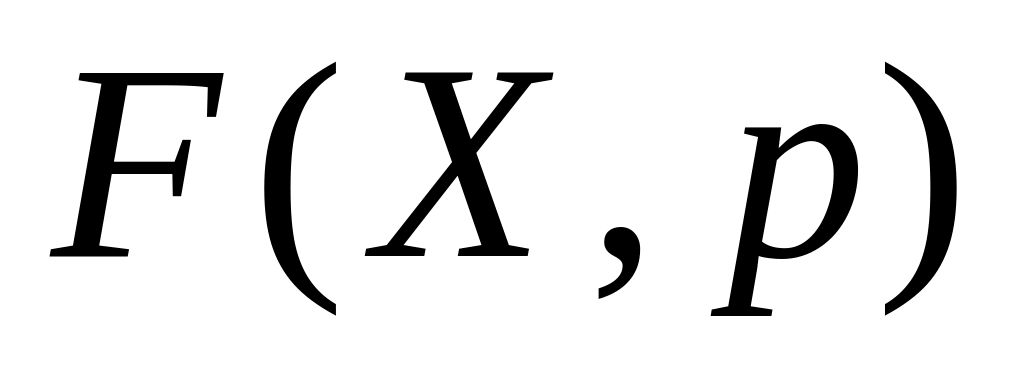принимает минимальное значение (задача оптимизации).

Рассматриваемая выше задача относится к третьей постановке задачи комбинаторного поиска.

Выбор метода решения задачи. Любые комбинаторные вычисления требуют предварительного анализа трудоемкости решения исходной задачи и используемых алгоритмов ее решения. Задачи обычно оцениваются с точки зрения размера, т.е. общего количества различных вариантов, среди которых требуется найти оптимальное решение, а алгоритмы оцениваются с точки зрения сложности. Исходя из выше приведенной концепции, решаемая задача относится к классу задач большой размерности.

Так, при рассмотрении нескольких десятков возможных вариантов электроснабжения и рассмотрении порядка возможных мест размещения генераторов, можно сформировать несколько десятков миллиардов возможных вариантов решения задачи [4], [5].

Кроме этого второй отличительной особенностью данной задачи является то, что возникает необходимость решения оптимизационной задачи, оптимизируя одновременно сразу несколько параметров, т.е. данная задача относится к классу задач многопараметрической оптимизации.

Третьей особенностью задачи, которая значительно усложняет ее решение, является то, что целевую функцию невозможно представить в аналитическом виде; для каждого возможного варианта решения задачи ее приходится вычислять, используя довольно сложный алгоритм; т.е. целевая функция задается алгоритмически.

Все методы комбинаторной оптимизации можно условно разделить на: точные и приближенные. К точным методам относятся: метод полного перебора, метод неявного перебора, метод ветвей и границ, метод динамического программирования и др. Чтобы понять все «прелести» точных методов решения задач комбинаторной оптимизации, остановимся на характеристике метода полного перебора [6], [7].

Полный перебор всех планов позволяет наверняка решить задачу. Другое дело, что для этого может понадобиться неприемлемо большое время. Только поэтому и существует разветвленная теория комбинаторных задач, основная цель которой – разработка и анализ эффективных, т.е. достаточно быстрых алгоритмов для различных частных случаев комбинаторных задач. Тем не менее, перебор планов остается наиболее универсальным методом решения. Если он не всегда пригоден для практических целей, то полезен для исследования задач, для сравнения с приближенными алгоритмами и т.п.

Считается, что конкретный алгоритм выполняет исчерпывающий перебор, если можно гарантировать, что не пропущен ни один план, который мог бы повлиять на результат.

Наиболее часто для организации перебора планов используется схема под названием перебор с возвратом. Перебор планов задачи можно представить как обход дерева перебора. Размер дерева перебора может быть очень большим. Достаточно часто при этом возможен такой эффект: комбинаторная задача для малой размерности решается достаточно просто, но при увеличении размерности быстро становится практически неразрешимой. Этот эффект получил название комбинаторного взрыва.

Логично сделать вывод, что полный перебор планов является весьма нежелательным способом решения комбинаторных задач, своего рода крайним средством при отсутствии более практичных алгоритмов. Следует использовать любую возможность, позволяющую либо существенно сократить перебор с учетом специфики конкретной задачи, либо вообще, когда такое возможно, отказаться от перебора и использовать иные методы решения.

Методы перебора и все их усовершенствования имеют один, но очень серьезный недостаток: время их работы экспоненциально растет при увеличении размерности задачи. Для решения практических задач это в большинстве случаев является неприемлемым. Других же подходов, пригодных сразу же для всех задач комбинаторного поиска, не имеется. Значит можно надеяться только на алгоритмы, учитывающие специфику конкретных задач.

Алгоритмы оптимизации, для которых имеются нетривиальные оценки возможного отклонения решения от оптимума, называются приближенными или субоптимальными.

Однако не всегда удается оценить погрешность метода. Вполне типична ситуация, когда используемый алгоритм дает достаточно приличные решения, однако нет никаких гарантий, что эти решения близки к оптимальным. Алгоритмы, основанные на нестрогих соображениях «здравого смысла» и не имеющие никаких гарантий близости к оптимальным решениям, называются эвристическими алгоритмами.

Одной из разновидностей эвристических алгоритмов являются популярные в последнее время генетические алгоритмы (ГА). По сути дела генетические алгоритмы являются оригинальной разновидностью алгоритмов случайного поиска с последовательным улучшением. Исследования показали, что внесение в такие методы элементов детерминированности дает значительное улучшение показателей. Детерминированность этих методов заключается в моделировании природных процессов отбора, размножения и наследования, происходящих по строго определенным правилам. Основным правилом при этом является закон эволюции: «выживает сильнейший», который обеспечивает улучшение находимого решения. Другим важным фактором эффективности эволюционных вычислений является моделирование размножения и наследования. Рассматриваемые варианты решений могут по определенному правилу порождать новые решения, которые будут наследовать лучшие черты своих «предков» [8].

Применим для решения вышесформулированной задачи методы генетического программирования.

Описание основных этапов работы генетического алгоритма. Для любого генетического алгоритма выделяются четыре основных этапа:

1) формирование начальной популяции;

2) синтез новых хромосом (операторы скрещивания и мутации);

3) целенаправленное изменение вновь полученных хромосом (операторы инверсии);

4) селекция текущей популяции.

Первый этап построения генетического алгоритма для решения данной задачи заключается в выборе возможной кодировки решения, т.е. в построении хромосомы определенной длины, каждый ген в которой занимает определенную позицию, и также имеет определенную длину. Длины каждого из генов, а также длина всей хромосомы будет напрямую зависеть от множеств . Зададимся одним вариантом электроснабжения, т.е. количеством одинаковых ИП, которые покроют полностью потребности потребителей электрической энергии. Пусть это будет число - число одинаковых ИП, участвующих в электроснабжении данного района. Зададимся также типоразмером ИП.

Геометрически любую хромосому можно представить, если представить нить с нанизанными на нее генами.

С помощью хромосом формируется в первую очередь начальная популяция.

Алгоритм формирования начальной популяции. Для успешной работы генетических алгоритмов важным является определение правил, по которым будет формироваться популяция в начальную эпоху своего существования, т.е. на момент времени . Основная парадигма, которая будет положена в основу этих правил, заключается в том, что в начальной популяции должен обязательно присутствовать весь генетический материал задачи; т.е. в нашем случае в начальной популяции должны обязательно присутствовать в качестве возможных мест размещения ИП все точки из множества .

Приведем общий вид хромосомы, используемой для решения данной задачи:

Значения	1	0	0	….	1	0
Возможные места размещения ИП (J)	1	2	3	….	(т-1)	т

Количество единиц в первой строке должно быть равно числу . Единица указывает на тот факт, что в данном возможном месте размещен ИП, ноль - ИП в этом месте нет. Во второй строке указано, в какой из возможных точек размещен данный ИП.

Целевая функция не зависит от стоимости ИП, т.к. эта составляющая будет во всех вариантах одинаковая. Хромосома физически представляет собой допустимое решение рассматриваемой задачи. Значение целевой функции, вычисленное для данной хромосомы это стоимость данного варианта электроснабжения.

Для решения конкретной задачи требуется однозначно отобразить конечное множество вариантов на множество строк подходящей длины. Генетический алгоритм за один шаг производит обработку некоторой популяции хромосом. Популяция G(t) на шаге представляет собой конечный набор строк:

, ,

где число особей (хромосом) в популяции, причем хромосомы в популяции не должны повторяться.

Алгоритм операции скрещивания (кроссинговера). Определяющим для работы генетических алгоритмов является наличие эффективной операции скрещивания. В качестве исходных данных имеем начальную популяцию, состоящую из хромосом. Выберем вариант полового размножения в популяции, т.е. случай, когда в создании новой дочерней хромосомы всегда участвуют две хромосомы. Выберем в качестве варианта отбора родительских хромосом турнирный отбор.

Будем использовать модифицированный оператор скрещивания, позволяющий учитывать специфику данной задачи. Покажем работу данного оператора на следующем примере: в задаче имеется 10 возможных мест размещения ИП и для покрытия суммарной мощности потребителей требуется 5 ИП. Пусть в результате турнирного отбора выбрано двое родителей:

Хромосома А-первый родитель

Значения	1	0	1	0	0	1	0	0	1	1
Возможные места размещения ИП	1	2	3	4	5	6	7	8	9	10

Хромосома В-второй родитель

Значения	1	0	0	1	0	1	1	1	0	0
Возможные места размещения ИП	1	2	3	4	5	6	7	8	9	10

Количество единиц в значениях хромосом одинаковое (первые строки хромосом) и равно 5, по количеству ИП, которые необходимо разместить.

Находим точки совпадения в хромосомах родителях (одинаковые гены). В результате получаем точки 1 и 6. Эти точки передаются в хромосомы- потомки без изменения. Генетическая информация, присутствующая в хромосомах обоих родителей, имеет горазло большую вероятность быть переданной потомкам. Будем предполагать, что эта информация передается со 100 % вероятностью.

Сжимаем затем хромосомы-родителей до ненулевых элементов в строке «значения» без учета совпадающих генов.

Хромосома А-первый родитель

Значения	1	1	1
Возможные места размещения ИП	3	9	10

Хромосома В-второй родитель

Значения	1	1	1
Возможные места размещения ИП	4	7	9

Выбираем случайным образом точку разрыва, пусть, например, эта точка будет точкой между первым и вторым генами. Далее, используя классический алгоритм операции скрещивания, получаем следующие хромосомы потомки:

Хромосома С-первый потомок

Значения	1	0	1	0	0	1	1	1	0	0
Возможные места размещения ИП	1	2	3	4	5	6	7	8	9	10

Хромосома D –второй потомок

Значения	1	0	0	1	0	1	0	0	1	1
Возможные места размещения ИП	1	2	3	4	5	6	7	8	9	10

Передачей потомкам одинаковых генов достигается эффект передачи потомкам более сильных генов, сжатие хромосом перед операцией скрещивания значительно ее упрощает.

Процедура мутации. Оператор мутации также служит для естественного отбора. Однако, вместо комбинирования родительских качеств, мутация вносит случайные изменения в одну из хромосом. После каждого скрещивания для каждой из вновь получившихся хромосом формируем «признак мутации»: генерируем случайное число от до , если это число меньше, чем коэффициент мутации, то запускаем процедуру мутации для этой хромосомы. Эта процедура заключается в следующем:

1. Случайным образом определяем ненулевой ген, который должен мутировать;

2. Заменяем этот ген на любой другой ненулевой, выбранный случайным образом из множества .

Оператор инверсии. Оператор инверсии изменяет характер связей между компонентами хромосомы. Он берёт хромосому, случайным образом выбирает в ней две точки разрыва и располагает в обратном порядке элементы, попавшие между точками разрыва.

Оператор селекции. Оператор селекции формирует новое поколение из хромосом с лучшими значениями целевой функции Z. Он уничтожает большую часть популяции и освежает генетический материал, пополняя популяцию большим количеством новых членов. В результате выполнения оператора селекции размер популяции нового поколения вновь становится равным PR.

При реализации генетического алгоритма в данной постановке приходится многократно реализовывать эвристический алгоритм оптимального закрепления потребителей за ИП. Прежде чем вычислить значение целевой функции для данного варианта решения, необходимо закрепить каждого потребителя за своим источником электрической мощности [9 - 11].

Другой важный момент генетического алгоритма - определение критериев останова. Обычно в качестве таковых применяются или ограничение на максимальное число эпох функционирования алгоритма, или определение его сходимости, путем сравнения приспособленности популяции на нескольких эпохах и остановки процесса поиска оптимального решения при стабилизации этого параметра.

Апробация работы генетического алгоритма оптимального размещения ип одинакового типоразмера в распределительной электрической сети.

В качестве примера рассматривается задача размещения трех двухтрансформаторных подстанций на территории некоторого района. В качестве исходных данных имеем:

1. места размещения потребителей электрической мощности,

2. нагрузки потребителей,

3. типоразмер источников питания,

4. возможные места размещения источников питания.

Сформулируем задачу таким образом, чтобы в исходные данные задачи заведомо попали точки оптимального размещения ИП. Для этого разобьем все электроприемники на три группы равной суммарной мощности и для каждой из групп найдем по формулам (5) условные центры электрических нагрузок (ЦЭН) [12].

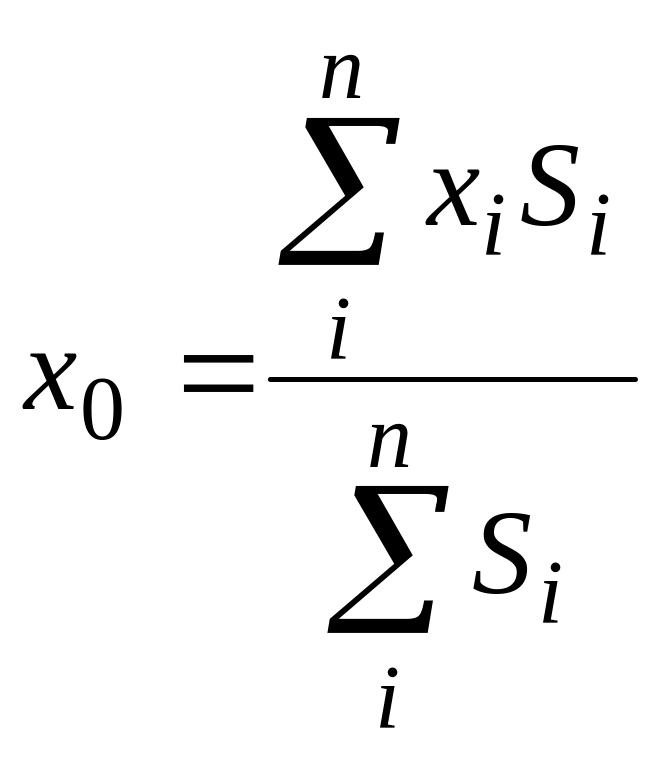
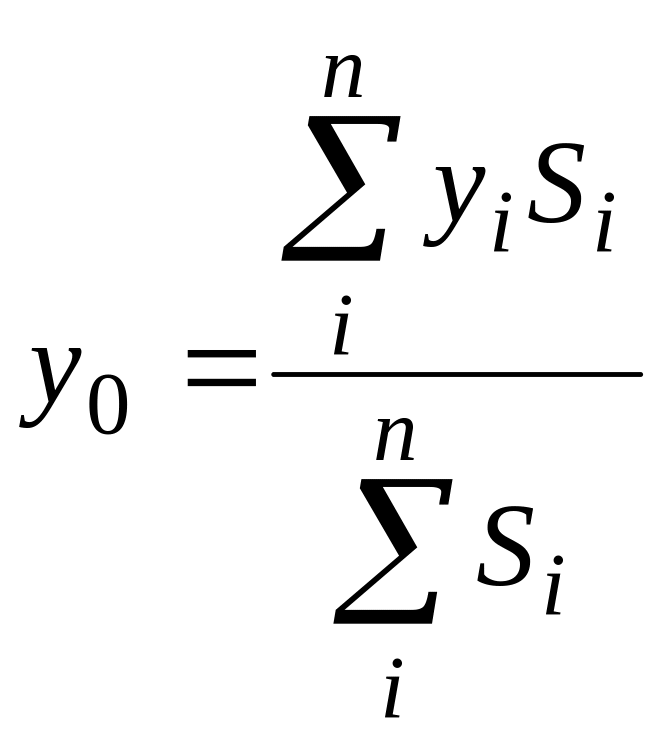(5)

В табл. 1-3 представлены данные для расчета соответствующих центров электрических нагрузок.

Таблица 1

Таблица для расчета центра электрических нагрузок по ТП-1

№	х (м)	y(м)	S (кВА)
1	30	120	100	3000	12000
2	90	30	120	10800	3600
3	150	150	100	30750	30750
4	90	180	123	11070	22140
5	30	210	145	4350	30450
6	210	60	170	35700	10200
7	240	120	100	24000	12000

Продолжение табл. 1

№	х (м)	y(м)	S (кВА)
8	240	180	50	12000	9000
9	180	240	67	12060	16080
10	150	270	20	3000	5400
			1100	146730	151620

.

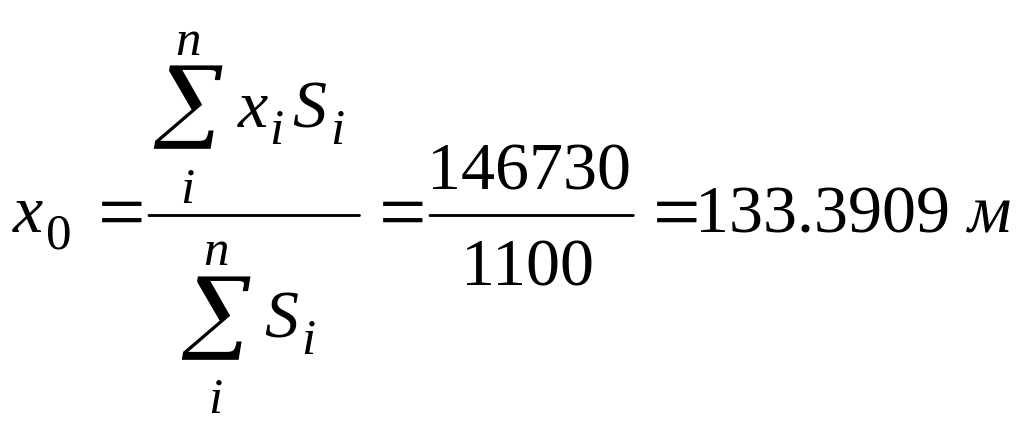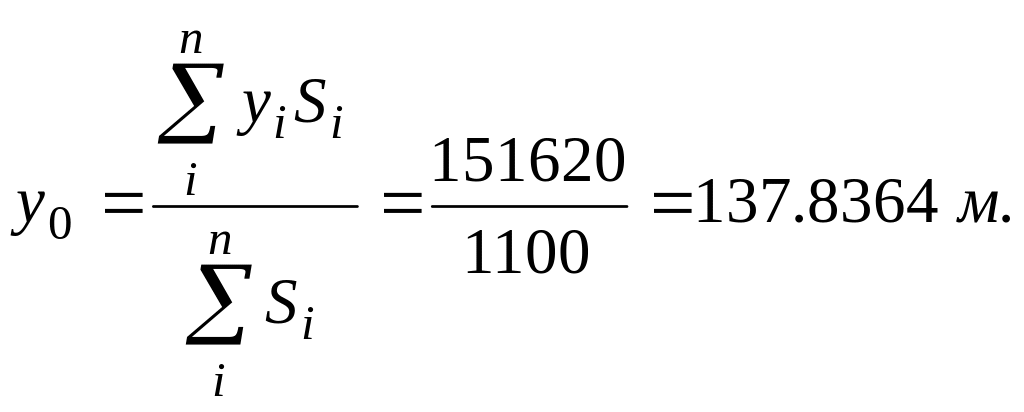
Таблица 2

Таблица для расчета центра электрических нагрузок по ТП-2

№	х (м)	y(м)	S (кВа)
1	420	450	150	63000	67500
2	450	510	220	99000	112200
3	540	450	212	114480	95400
4	600	330	130	78000	42900
5	420	330	190	79800	62700
6	420	390	100	42000	39000
7	510	390	98	49980	38220
			1100	526260	457920

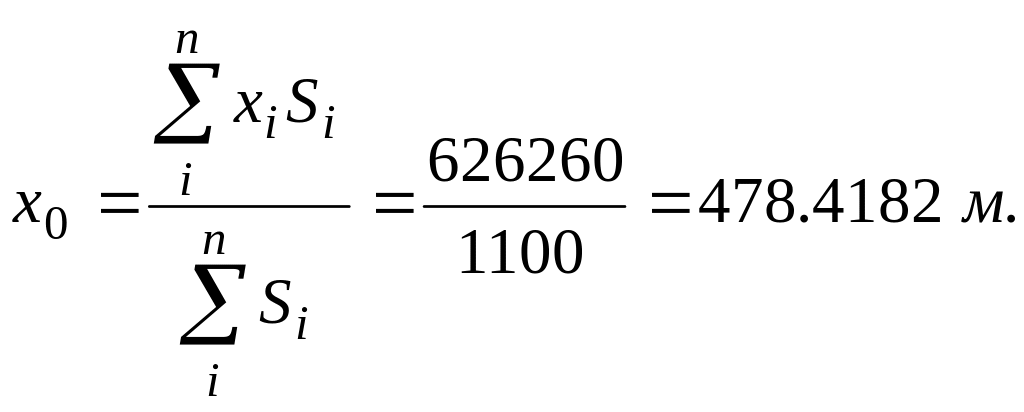
Таблица 3

Таблица для расчета центра электрических нагрузок по ТП-3

№	х (м)	y(м)	S (кВа)
1	660	270	104	68640	28080
2	600	210	217	130200	45570
3	780	270	123	95940	33210
4	690	180	314	216660	56520
5	660	120	89	58740	10680

Продолжение табл. 3

№	х (м)	y(м)	S (кВа)
6	780	120	67	52260	8040
7	810	210	86	69660	18060
8	570	90	100	57000	9000
			1100	749100	209160

.

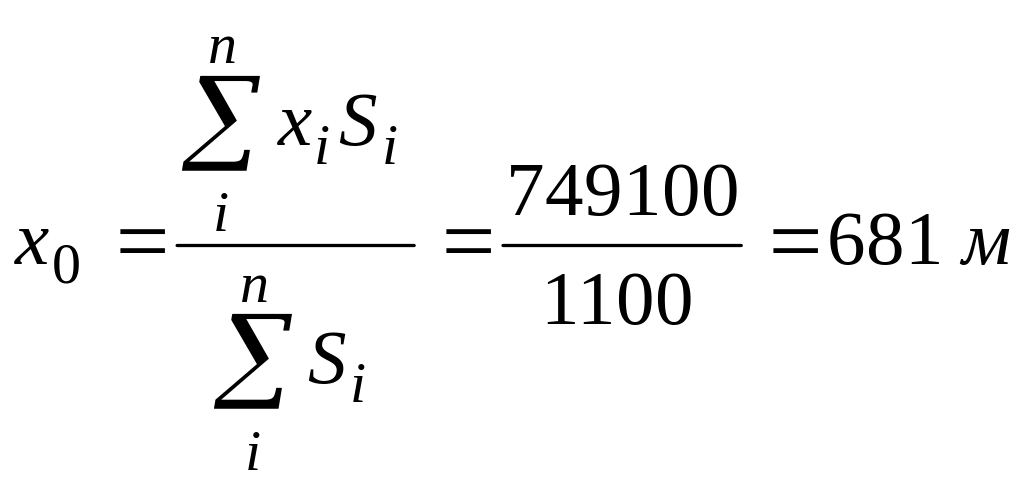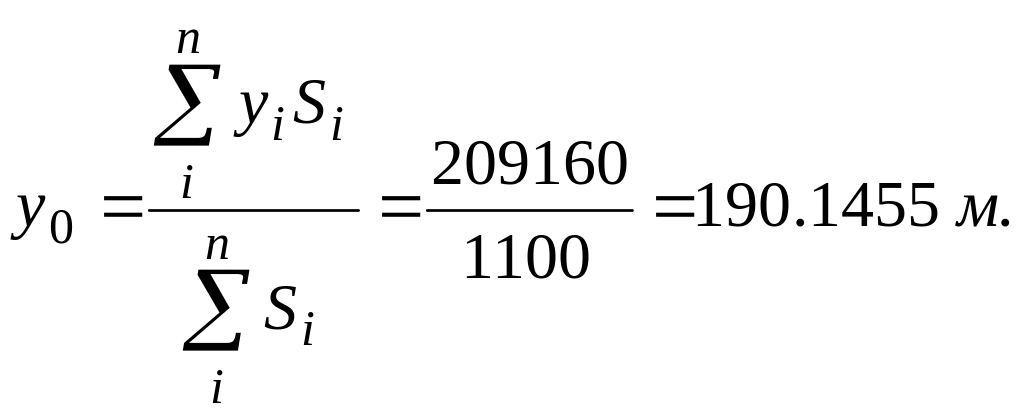
Зная места расположения потребителей, а также места размещения центров электрических нагрузок, легко подсчитать значения минимума функции приведенных затрат по формуле (4).

Затраты в радиально-лучевую сеть для ТП-1 равны .

Затраты в радиально-лучевую сеть для ТП-2 равны

Затраты в радиально-лучевую сеть для ТП-3 равны .

Суммарные затраты по всем трем ТП равны .

Зададимся возможными местами расположения ТП, представленными в табл. 4:

Таблица 4