Поляризуемость и ее составляющие (1, 2,3) (Леше а.,1987). Для перевода в si значения  необходимо умножить на 40

Молекула	1, , м3	2, , м3	3, , м3	, , м3
CO2	4,10	1,93	1,93	2,65
NH3	2,42	2,18	2,18	2,26
H2S	4,21	3,21	3,93	3,78
SO2	5,49	2,72	3,49	3,90
HCl	3,13	2,39	2,39	2,64
Cl2	6,6	3,62	3,62	4,61

Ориентационная и деформационная поляризации показаны на рис. 4, где Е₀ – напряженность внешнего электрического поля, Е  поле, создаваемое ориентируемыми зарядами.

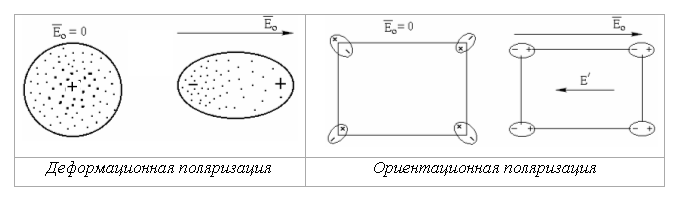
Рис. 4. Деформационная и ориентационная поляризации

В табл. 2 и 3 приведены значения поляризуемостей некоторых молекул.

Таблица 2

Средние значения поляризуемости молекул (П.Эткинс, Т. 2, 1980). Для перевода в SI необходимо умножить значения ₀ ( 8.85419^12 Ф/м)

Молекула	, 10-30, м3	Молекула	, 10-30, м3
СО2	33,3	C6H6	129,7
Н2О	18,6	H2	9,93
NH3	27,8	N2	22,1
Cl4	127	He	2,5
CH4	32,7	Ar	20,1

Таблица3

Средние значения поляризуемости молекул (Кр. справ., физ.-хим. величин, 1983). Для перевода в SI значения  необходимо умножить на 4₀

Молекула	, 10-30, м3	Молекула	, 10-30, м3
СО2	2,594	HCl	2,561
Н2О	1,444	H2	0,802
NH3	2,145	N2	1,734
SO2	3,774	He	0,203
Cl4	10,14 - 10,04	Ar	1,626
H2S	3,642	Xe	3,999

Диэлектрическая восприимчивость вещества _d

Диэлектрическая восприимчивость – поляризуемость единицы объема вещества. В гауссовой системе единиц _dn. В СГСЭ диэлектрическая восприимчивость – величина безразмерная. В Международной системе единиц (СИ) диэлектрическая восприимчивость записывается в виде

_d  (n/₀). (4)

В СИ диэлектрическая восприимчивость также является безразмерной величиной, так как _(СИ)  4₀_(СГСЭ).

Молярная поляризация вещества Р_м

Молярная поляризация вещества – поляризуемость моля частиц – определяется по формуле

Р_м  _d V₀  nV₀/₀  (N_А/₀). (5)

Молярная поляризация вещества в Си и СГСЭ измеряется в единицах объема на моль: в СИ – м³моль^-1, в СГСЭ – в см³моль^-1.

У полярного диэлектрика по сравнению с неполярным молярная поляризация в значительной степени зависит от температуры. С повышением температуры поляризуемость неполярной молекулы несколько уменьшается вследствие уменьшения напряженности поля в веществе. (Следует отметить, что данный вопрос практически не изучен.).

При внесении молекулы в электрическое поле происходит изменение ее дипольного момента: полярные молекулы увеличивают значение дипольного момента от  до р, неполярные молекулы приобретают индукционный дипольный момент. Дополнительный (индукционный) дипольный момент появляется благодаря деформационной поляризуемости молекул и называется деформационным дипольным моментом р_деф:

р_деф.i _деф.i F_i, (6)

где _деф.i – деформационная поляризуемость i-й молекулы; F_i  напряженность электрического поля в месте расположения i-й молекулы.

Деформационная поляризуемость молекулы не является постоянной величиной. В сильных электрических полях (в лазерных лучах, внутри вещества) деформационная поляризуемость молекулы (при допущении, что в слабых полях _деф = _эл) определяется по формуле

_деф = _эл + (1/2!)₁ F + (1/3!)₂ F² + …, (7)

где _i  гиперполяризуемость молекулы i-го порядка. Подставив (7) в выражение (6), получим Выражение для р_деф может быть представлена в виде

р_деф =_элF + (1/2)₁F² + (1/6)₂F³+... (8)

В случае слабых электрических полей _эл _деф, поэтому

р_деф  _элF. (9)

Из выражения (9) следует, что поляризуемость молекулы представляет собой физическую величину, равную индукционному дипольному моменту, появляющемуся в поле единичной напряженности. Следовательно, поляризуемость в СИ измеряется в Клм²В^-1 (Фм²) или в Кл²м²Дж^-1 (Atkins P.W.,1990), в СГС – в единицах объема, т. е. в см³:

1 = 1p/1F = 1 ед. СГСЭ_q  1 ед. L СГСЭ_l / 1 ед. СГСЭ_q / 1ед. L² = L³.

Нетрудно заметить, что поляризуемость в СИ и СГСЭ соотносятся следующим образом:

_(СИ)  4₀_(СГСЭ)10^-6. (10)

Следует отметить, что в учебной литературе поляризуемость молекулы в СИ часто измеряется единицах объема (м³) и называется геометрической поляризуемостью. Использование двух понятий поляризуемости нежелательно, так как в этом случае формулы для характеристик поляризации, связанные с поляризуемостью, имеют различный вид:

p_деф.i _деф.i F_i; p_деф.i  ₀_деф.i F_i; р _деф.i  4₀_деф.i F_i.

Именно по этой причине в большинстве случаев используется гауссова система единиц.

Примечание. Некоторые соотношения и принятые обозначения характеристик поляризации в СИ и СГСЭ (Киттель Ч., 1987):

(СГСЭ): D  E + 4P    Е   p_деф / F; P  E;

(СИ) : D  ₀E + P  ₀  )₀   p_деф / F; P  ₀E;

_(СИ)  _(СГСЭ);  _(СИ)  4 _(СГСЭ); _(СИ)  4₀_(СГСЭ) 10^-6..

Дипольный момент молекулы

Дипольный момент молекулы в веществе принято обозначать р, а дипольный момент молекулы в вакууме – . При внесении молекулы в электрическое поле распределение зарядовой плотности молекулы изменяется: неполярные молекулы приобретают индукционный дипольный момент р_деф, полярные молекулы увеличивают значение дипольного момента от  до р. В общем случае величина дипольного момента i-й молекулы в среде

р_i  _I + р_деф.i. (11)