1. Цель и содержание работы

Целью работы является изучение зависимости сопротивления примесного полупроводника от температуры. Содержание работы состоит в определении энергии активации электронов и температурного коэффициента сопротивления для термисторов типа ММТ-1 и КМТ-4.

2. Краткая теория работы

По величине удельной проводимости полупроводники занимают промежуточное положение между металлами и изоляторами (диэлектриками). Полупроводники имеют ряд общих свойств как с диэлектриками, так и с металлами:

1. Проводимость металлов имеет электронную природу. Диэлектрические кристаллы обладают ионной проводимостью. В этом отношении полупроводники схожи с металлами: как и в металлах, проводимость большинства полупроводников имеет электронное происхождение.

2. При нагревании проводимость металлов уменьшается, а проводимость полупроводников, также как и диэлектриков, резко возрастает. Однако известны некоторые полупроводники, для которых зависимость проводимости от температуры имеет такой же характер, как и у металлов.

3. Проводимость металлов уменьшается при введении примесей. Проводимость диэлектриков, наоборот, при введении примесей возрастает. В этом отношении полупроводники похожи на диэлектрики: включение примесей приводит к резкому увеличению проводимости полупроводников.

При не слишком высоких напряженностях поля (менее 1000 В/см) в полупроводниках выполняется закон Ома:

j=γ*Ε , (А)

где j – плотность тока,

γ – удельная проводимость,

Е – напряженность поля.

Так как в полупроводнике имеются носители заряда двух типов – электроны и дырки, то

, (В)

где n и υ – концентрация и скорость упорядоченного движения носителей заряда.

Вводя подвижность носителей заряда , т. е. скорость их направленного движения в поле единичной напряженности, получим из (А) и (В) выражение для удельной проводимости полупроводника:

.

Температурная зависимость проводимости полупроводника определяется изменением концентрации и подвижности электронов и дырок с температурой.

С повышением температуры возрастает число столкновений в единицу времени и подвижность носителей заряда падает.

Подвижность электронов в полупроводниках, как и в металлах, сравнительно слабо зависит от температуры. Если в металлах b~T ^-1 , то в полупроводниках, в зависимости от характера связи атомов в решетке, b~T ^-3/2 или b~T ^-5/2 .

Вследствие малой концентрации электронов проводимости в полупроводниках, они подчиняются классической статистике Максвелла-Больцмана. Поэтому в области низких температур для концентрации электронов (или дырок) в зоне проводимости с одним видом примеси (донорная или акцепторная) имеем:

, (1)

где А – коэффициент, не зависящий от Т,

∆W – энергия активации примеси, т. е. энергетический интервал между донорным уровнем нижним краем зоны проводимости (или акцепторным уровнем и верхним краем валентной зоны) (рис. 1),

k – постоянная Больцмана.

Так как подвижность b и множитель T^3/2 в формуле (1) с температурой меняются медленно по сравнению с экспоненциальным членом и в противоположные стороны, то в рассматриваемой области температур удельная проводимость примесного полупроводника изменяется по экспоненциальному закону

. (2)

Здесь b – величина , практически постоянная в данной области температур.

Прологарифмируем уравнение (2):

.

Рис. 1

Энергетические диаграммы.

а – электронный полупроводник

б – дырочный полупроводник.

Откладывая по оси абсцисс , а по оси ординат , получим в области относительно низких температур прямую, угловой коэффициент которой определяется энергией активации примеси (область 1 на рис. 2).

Рис. 2

Температурная зависимость удельной проводимости

полупроводника с одним видом примеси.

При достаточно высокой температуре почти все носители тока перейдут с примесных уровней в зону проводимости, и, следовательно, концентрация свободных электронов (или дырок) будет оставаться постоянной (область II, называемая областью «истощения примеси») вплоть до температур, при которых начнутся переходы электронов из валентной зоны в зону проводимости (собственная проводимость).

Примесные полупроводники, используемые в полупроводниковых приборах – диодах и транзисторах, - работают в области II, так что их удельная проводимость слабо (по сравнению с экспоненциальной зависимостью) меняется при изменении температуры.

В области собственной проводимости

,

и при графическом построении в полулогарифмических координатах получается прямая (область III на рис. 2), наклон которой определяется шириной запрещенной зоны ∆W₀ (см. рис. 1)/

Помимо рассмотренных атомарных полупроводников (германий, кремний, селен) существует широкий класс полупроводников, представляющих собой соединения типа M_mR_r (окислы, сульфиды, селениды, теллуриды и т. д.).

Здесь М – символ металла,

R – символ металлоида,

А m и r – соответствующие индексы в химической формуле (например, СО₂, TiO₂ m=1, r=2).

Обозначим N_M – общее число ионов металла в кристаллической решетке, а N_R – общее число ионов металлоида; в идеальной решетке выполняется так называемое стехиометрическое соотношение:

.

В полупроводниках типа M_mR_r под «примесью» понимают всякое отклонение от стехиометрического соотношения. Реальная решетка такого вида содержит, вообще говоря, дефекты двух типов:

А) электроположительные, представляющие собой пустые металлоидные узлы и междуузельные металлические ионы, и

Б) электроотрицательные – пустые металлические узлы и междуузельные металлоидные ионы.

Для таких полупроводников зависимость удельной проводимости от температуры оказывается более сложной. Однако вся область температур может быть разбита на отдельные участки, внутри которых общая сложная формула вырождается в простую экспоненциальную зависимость, выражаемую формулой (2). Эти участки изображаются на графике в полулогарифмических координатах линейными отрезками (рис.3):

Ри с. 3

Зависимость удельной проводимости от температуры для полупроводника типа N_mR_r с «примесями» двух видов.

Кривые перенумерованы в порядке возрастания концентрации дефектов в образцах.

Величины b и ∆W остаются постоянными внутри каждого данного участка, но меняются при переходе от одного участка к другому. Это отнюдь не означает, однако, что энергия активации ∆W является функцией температуры, т. е. что работа освобождения связанного электрона (или дырки) меняется с температурой. Это означает лишь то, что подача электронов в зону проводимости (или дырок в валентную зону) в разных областях температур происходит с различных энергетических уровней (рис. 4).

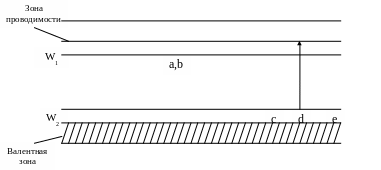
Рис. 4

Энергетическая диаграмма полупроводника типа M_mR_r .

На рис. 3 области, в которых проводимость обусловлена электронами, поступающими в зону проводимости за счет переходов электронов, помеченных буквами a, b, c, d, e, на рис. 4 обозначены теми же буквами.

В этой работе исследуются термисторы – нелинейные полупроводниковые сопротивления с электронной проводимостью. Величина сопротивления термистора R резко зависит от температуры.

Наибольшее распространение имеют термисторы с отрицательным температурным коэффициентом сопротивления

.

Они изготавливаются из твердых поликристаллических полупроводниковых материалов: смесей двуокиси титана с окисью магния, окислов марганца, меди, кобальта и никеля и т. д.

Основными параметрами термисторов являются:

1. Сопротивление образца при Т=20°С.

2. Величина температурного коэффициента сопротивления в процентах на один градус изменения температуры.

3. Энергия активации электронов ∆W, определяющая его температурную чувствительность.

4. Максимально допустимая температура, выше которой характеристики термистора становятся нестабильными.

Термосопротивления широко применяются для измерения температуры, а также для компенсации температурных изменений параметров электрических цепей.

Из формулы (2) следует, что сопротивление термистора в области рабочих температур может быть представлено в виде:

, (3)

где С – величина, постоянная в рабочем интервале температур.

Следовательно:

,

где 0,43 = lg e = 1/ln 10 – модуль перевода натуральных логарифмов в десятичные.

Последнее выражение в координатах lg R и 1/T представляет собой уравнение прямой, по угловому коэффициенту которой

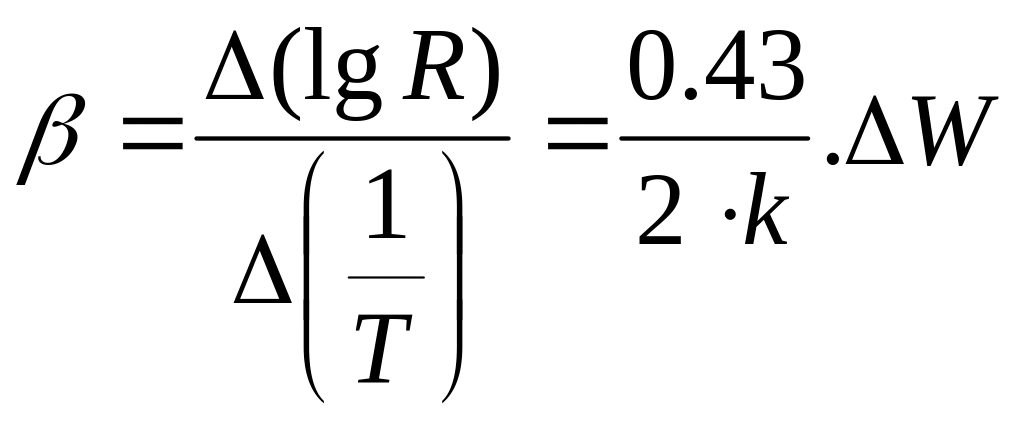
можно определить энергию активации электронов.

Подставляя в выражение для углового коэффициента значение постоянной Больцмана k=0.86*10^-4 эВ/град, найдем энергию активации

эВ. (4)

Дифференцируя выражение (3) и используя определение температурного коэффициента α, получим

(5)