Содержание отчета

1. Формулировка цели работы.

2. Результаты измерений и расчетов (с погрешностями) по методу фигур Лиссажу в табличной форме.

3. Результаты расчетов периода Т_б и частоты биений  (с погрешностями).

4. График зависимости А_б = F[cos( t/2)].

Контрольные вопросы

1. Для чего используется электронный осциллограф?

2. Каково назначение основных блоков осциллографа?

3. Каковы устройство и принцип работы электронно-луче­вой трубки?

4. Для чего служит генератор развертки?

5. В чем суть метода фигур Лиссажу?

6. Как возникают биения?

7. Как проверить формулу для амплитуды биений?

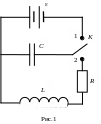
Работа 2. Электромагнитные колебания в простом колебательном контуре

Цель работы – исследовать зависимость периода колебаний от индуктивности, а также емкости и добротности контура от активного сопротивления.

Общие сведения

Электрический колебательный контур состоит из емкости С, индуктивности L и активного сопротивления R (рис.1). Когда переключатель K поставлен в положение 1, батарея  сообщает конденсатору некоторый заряд q. При перебрасывании переключателя в положение 2 конденсатор начинает разряжаться через катушку, в цепи возникает ЭДС самоиндукции, под действием которой конденсатор разряжается не мгновенно. Ток в контуре не прекращается и после разрядки его до нуля, а продолжает протекать в прежнем направлении в течение некоторого времени, вследствие чего на обкладках конденсатора появляется заряд, противоположный начальному по знаку. Таким образом, конденсатор оказывается перезаряженным, и в контуре вновь протекает процесс его разрядки, но в обратном направлении. Такие периодические изменения зарядов, напряжений и токов в контуре носят название электромагнитных колебаний. При этом происходит непрерывный переход энергии электрического поля в конденсаторе в энергию магнитного поля в катушке и обратно. В произвольный момент времени полная энергия колебаний

,

где U и i – мгновенные значения разности потенциалов и тока.

В те моменты времени, когда конденсатор полностью разряжен (U = 0), ток достигает максимального значения I_m, и полная энергия контура равна энергии магнитного поля:

.

Полная энергия колебаний постепенно уменьшается, так как электрическая энергия благодаря сопротивлению R непрерывно превращается в тепловую и рассеивается в окружающее пространство.

Составим дифференциальное уравнение колебаний в контуре. Пусть q – мгновенное значение заряда на обкладках конденсатора, а U – разность потенциалов между обкладками в тот же момент времени. Тогда полное напряжение в цепи равно сумме действующих ЭДС. Так как в цепи действует только ЭДС самоиндукции

,

то

.

Подставив в это равенство значения и , получим

. (1)

Разделим обе части уравнения (1) на L и введем обозначения:

; , (2)

где  – коэффициент затухания; ₀ – собственная частота колебаний контура.

Тогда дифференциальное уравнение колебаний примет вид

.

Это уравнение – линейное дифференциальное уравнение второго порядка с постоянными коэффициентами, и вид решений этого уравнения зависит от соотношения между коэффициентами. Положим, что (случай малых затуханий), тогда

, (3)

где q₀ – максимальное значение заряда на обкладках конденсатора; – амплитуда затухающих колебаний;  – начальная фаза колебаний;  – частота затухающих электрических колебаний,

. (4)

При R = 0 и  = 0

,

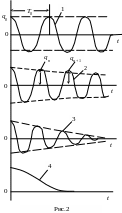
а период этих колебаний (рис.2, кривая 1)

.

В случае затухающих колебаний R  0 (рис.2, кривая 2) и период

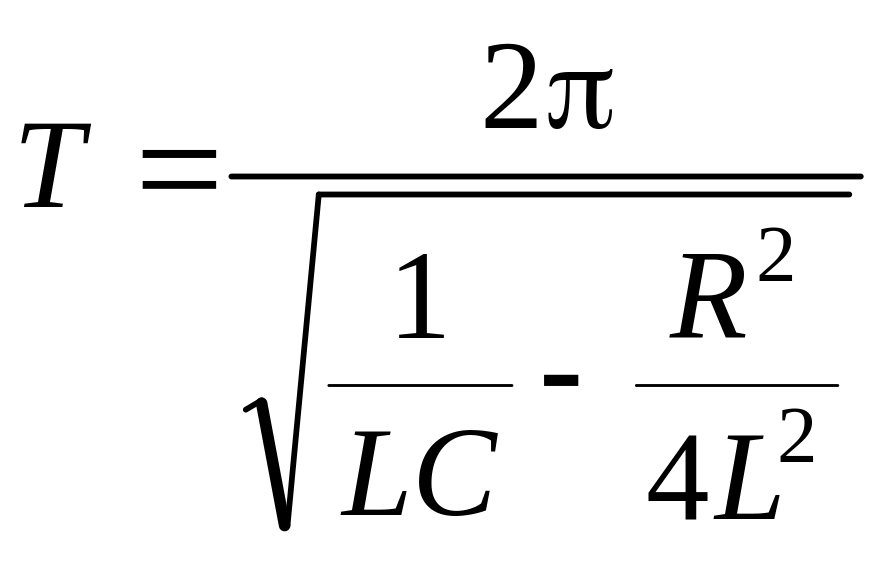. (5)

Уравнение (3) является аналитическим выражением затухающих колебаний. Большему значению коэффициента  соответствует кривая 3 (рис.2). Промежуток времени  = 1/, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации. Хотя затухающие колебания не являются периодическим процессом в строгом смысле этого слова, они обладают определенной повторяемостью в том смысле, что максимальные и минимальные значения заряда, а также тока и напряжения достигаются через одинаковый промежуток времени. Этот промежуток времени и называется периодом Т затухающих колебаний.

Как следует из (4), при   ₀ колебаний в контуре не будет. Разряд конденсатора будет апериодическим (рис.2, кривая 4).

Для выяснения физического смысла коэффициента  рассмотрим тепловые потери W_R на сопротивлении R за полупериод Т/2:

,

где – среднее за период значение тепловой мощности, выделившейся на сопротивлении R, для синусоидального тока

.

Полный запас энергии колебательного контура

.

Отношение энергии, израсходованной в контуре за полупериод на нагревание W_R (тепловые потери), к энергии колебаний W_L с учетом (2):

,

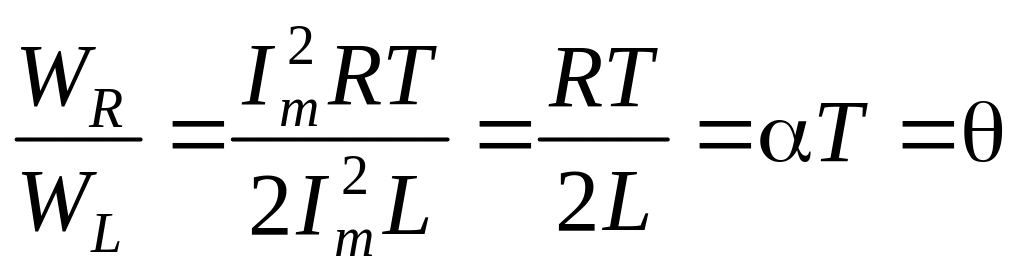где  называется логарифмическим декрементом, который вместе с коэффициентом затухания характеризует потери энергии в контуре.

определим логарифмический декремент иначе. Пусть q_n и q_n + 1 – амплитуды заряда конденсатора в момент времени t_n и t_n + 1 (рис.2, кривая 2), причем t_n + 1 = t_n + T. Тогда ; и, следовательно,

.

Видно, что отношение последующих амплитудных значений заряда не зависит от номера максимумов и является постоянной величиной для данного контура.

Логарифмический декремент контура – это натуральный логарифм отношения последующих амплитуд заряда конденсатора:

. (6)

В радиотехнической практике чаще пользуются величиной, обратно пропорциональной логарифмическому декременту  и называемой добротностью

, (7)

где N_е – полное число колебаний, совершаемых за время релаксации.

Чем выше добротность, тем медленнее рассеивается запас энергии контура.

Если напряжение U подать на вертикальный вход осциллографа, то на экране появятся быстро следующие друг за другом тождественно расположенные кривые, которые для глаза сливаются в единую. При надлежащем подборе частоты горизонтальной развертки эта кривая будет неподвижной. В рабочей схеме (рис.3) предусмотрена возможность включения конденсаторов с различной емкостью С. Индуктивность L катушки можно менять, вдвигая и выдвигая сердечник, а величина R изменяется магазином сопротивлений.