8.12. Расход газа

При изучении течения газа по проточной части ГТД важно знать секундный расход газа через двигатель, так как секундный расход газа определяет тягу двигателя.

Ранее отмечалось, что газодинамическая функция относительной плотности тока газа q(λ) характеризует расход газа.

Величина q(λ) связана с расходом газа следующим образом:

. (8.61)

Подставляя в (8.61) значение ρ_кр и с_кр из (8.34) и (8.35) и после преобразований получим

, (8.62)

где т – коэффициент, зависящий от свойств газа, определяется по формуле

. (8.63)

Для воздуха [R = 287 Дж/(кг∙К)] при k = 1,4 т = 0,0404 (кг∙К/Дж)^0,5, а для газа [R = 288 Дж/(кг∙К)] при k = 1,33 т = 0,0396 (кг∙К/Дж)^0,5.

Иногда расход газа удобно выражать через статическое давление p. В этом случае используют газодинамическую функцию

. (8.64)

Нетрудно увидеть, что

(8.65)

Зависимости q(λ) и Y(λ) показаны на рис. 8.20.; следует обратить внимание на то, что каждому значению q(λ) соответствует два аргумента: q₁(λ) < 1 (или М₁ < 1) и q₂(λ) > 1 (или М₂ > 1); при λ = 1 (в критическом сечении потока) q(λ) = 1.

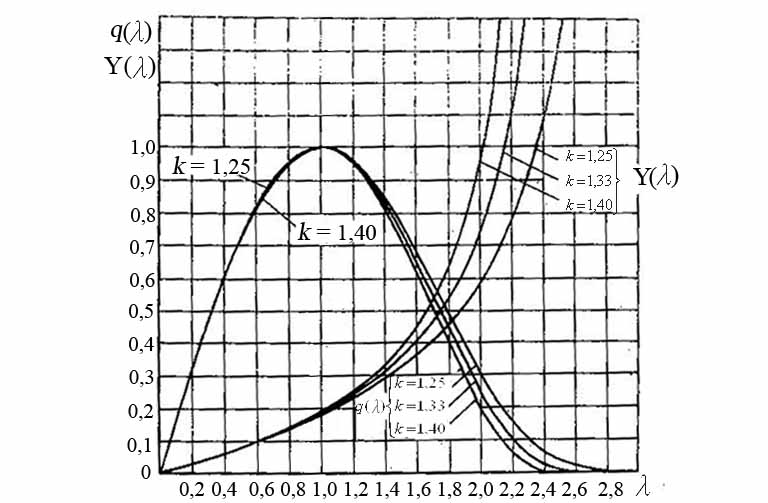
Рис. 8.20. Газодинамические функции, характеризующие расход газа

В соответствии с уравнением неразрывности расход газа в любом сечении канала остается постоянным, поэтому определим его для выходного сечения дозвукового сопла и выясним влияние на расход газа условий полёта. Для выходного сечения сопла величина расхода газа определяется по формуле:

G_В = F_c ∙ c_c ∙ ρ_c.

Скорость газа определим по формуле 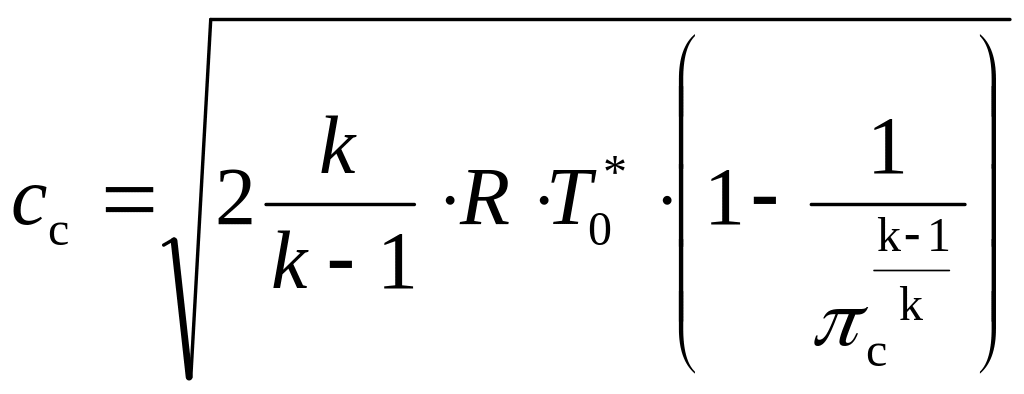, а ρ_с – из соотношений 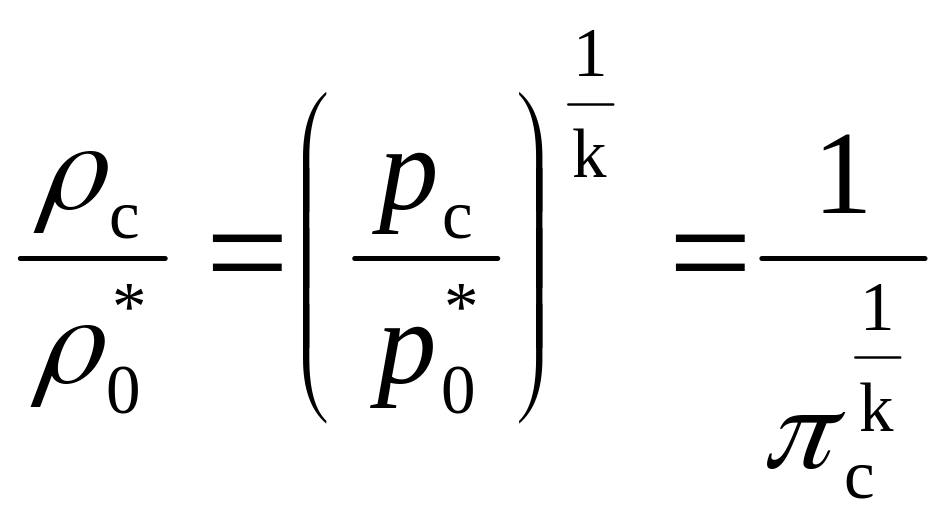. Учитывая, что , после простых преобразований получим следующее уравнение секундного расхода газа:

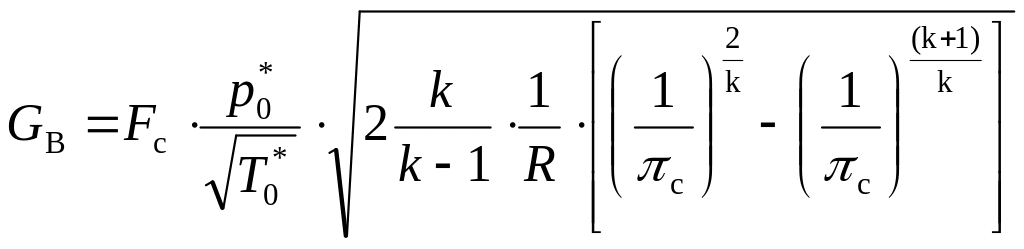. (8.66)

Из полученной формулы (8.66) видно, что расход газа (воздуха) через выходное сечение сопла зависит от его площади F_с, полных параметров на входе в сопло , , степени понижения давления газа в сопле π_c и рода рабочего тела (k, R).

При изменении скорости, высоты полета и режима работы ГТД изменяются параметры на входе в сопло ( , и давление окружающей атмосферы – p_H), поэтому выясним влияние этих параметров на расход газа.

Рассмотрим вначале влияние на расход газа атмосферного давления при условии, что параметры и не изменяются, а в сопле происходит полное расширение газа, т. е. p_с = p_H (для этого сопло должно иметь регулируемую площадь F_с). При этом π_c = /p_с = /p_H , поэтому изменение атмосферного давления вызовет изменение π_c.

График зависимости расхода газа от 1/ π_c представлен на рис. 8.21. Из графика видно, что при p_H = (π_c = 1) расход газа будет равен нулю, так как скорость потока в выходном сечении сопла равна нулю. Снижение давления окружающей атмосферы приведет к возрастанию степени расширения газа в сопле π_c. При этом растёт скорость истечения газа из сопла, но одновременно снижается его плотность. Однако вначале скорость растёт быстрее, чем снижается плотность, что приводит к увеличению расхода газа.

При достижении критической степени понижения давления (π_c = π_кр) расход газа будет максимальным, а скорость потока становится равной местной скорости звука. Если π_c увеличивать и дальше (π_c > π_кр), расход газа должен уменьшаться (штриховая линия на рис. 8.21.), так как при этом возрастание скорости происходит медленнее, чем уменьшение плотности. В действительности расход газа при π_c > π_кр остается постоянным, равным максимальному значению, так как сигналы об уменьшении давления окружающей атмосферы не могут пройти внутрь сопла через поток, движущийся со скоростью звука.

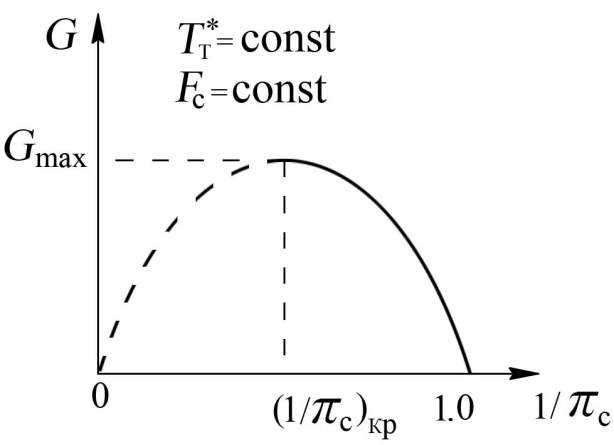
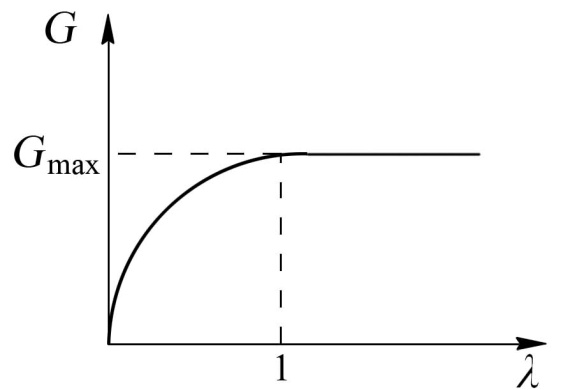
Рис. 8.21. Зависимость Рис. 8.22. Зависимость

расхода газа от 1/ π_с расхода газа от λ

Таким образом, при π_c ≥ π_кр в выходном сечении суживающегося сопла параметры потока становятся критическими, а расход газа – максимальным (критическим). В суживающемся – расширяющемся сопле (рис. 8.1,в.) при π_c > π_кр в выходном сечении скорость потока будет сверхзвуковой. Однако расход газа останется постоянным, равным максимальному, который достигается в критическом сечении сопла.

Для определения критического расхода газа можно воспользоваться формулой (8.62), в которой произвести замену: p^* = , Т^* = , F = F_кр и q (λ) = 1 или формулой (8.66), где после замены π_c на

и после преобразований получим один и тот же результат, а именно:

. (8.67)

Из этой формулы следует, что G_max зависит от площади критического сечения сопла F_кр, полных параметров , на входе в сопло и свойств газа (k, R).

Рассмотрим зависимость расхода газа от и . Предположим, что давление окружающей среды p_H и температура не изменяются, а давление возрастает. Это возможно при увеличении скорости полёта или частоты вращения ротора ГТД, а также при уменьшении высоты полёта. Расход воздуха в этом случае увеличится вследствие роста его плотности и скорости истечения с_с в выходном сечении сопла (при π_c < π_кр). После достижения π_c критического значения увеличение не вызовет увеличения с_с, скорость на выходе останется постоянной, но плотность газа увеличится из – за роста , поэтому расход газа тоже возрастёт. При уменьшении скорости полёта или частоты вращения ротора ГТД, при увеличении высоты полета снижается, что вызывает уменьшение расхода газа. Если температура увеличится при условии постоянных значений p_H и , расход газа уменьшится. Это объясняется более быстрым снижением плотности газа по сравнению с увеличением скорости истечения газа из сопла, так как плотность изменяется обратно пропорционально первой степени температуры , а скорость пропорциональна . В результате расход газа согласно формуле (8.67) изменяется обратно пропорционально .

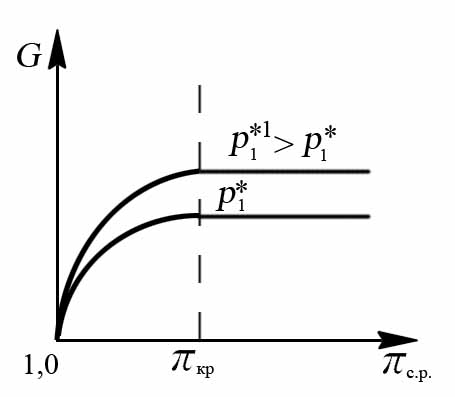
Рис. 8.23. Зависимость G = f (π_c.р.) при различных значениях давления

на входе в сопло

На рис. 8.23. показана зависимость расхода газа от располагаемой степени понижения давления при различных постоянных значениях . При π_c.р. = 1 течение газа в сопле отсутствует и G = 0. Повышение π_c.р. в области 1 < π_c.р. ≤ π_кр приводит к увеличению расхода газа за счёт роста скорости истечения. При π_c.р. > π_кр изменение величины π_c.р. (за счёт p_H) не влияет на расход газа, так как в этом случае параметры потока в сопле остаются неизменными, несмотря на изменение давления окружающей среды p_H. С увеличением давления на входе в сопло расход газа возрастает на всех режимах работы сопла как при 1 < π_c.р. ≤ π_кр, так и при π_c.р. > π_кр.