8.11. Режимы работы сверхзвукового сопла (сопла Лаваля)

Сопла Лаваля применяются в тех случаях, когда необходимо получение сверхзвуковых скоростей истечения. Сверхзвуковое сопло может работать на расчётном и нерасчётном режимах. В отличие от дозвукового сопла в сверхзвуковом сопле при определённом условии могут возникнуть два нерасчётных режима:

а) режим недорасширения (p_с > p_Н);

б) режим перерасширения (p_с < p_Н).

Сверхзвуковые скорости истечения могут быть достигнуты, если располагаемая степень понижения давления превосходит критическую величину. Поэтому далее мы будем рассматривать процесс истечения из сопла Лаваля при условии, что π_с.р. > π_кр.

8.11.1. Изменение параметров потока вдоль сопла Лаваля

При идеальном энергоизолированном течении газа параметры потока изменяются вдоль сопла Лаваля так, как показано на рис. 8.15. В суживающейся части сопла поток разгоняется до скорости звука, которая достигается в критическом (минимальном) сечении сопла. Течение газа и изменение параметров потока до критического сечения сопла полностью аналогично течению в суживающемся сопле при π_с.р. ≥ π_кр (см. рис. 8.13.). В расширяющейся части сопла происходит разгон сверхзвукового потока. Скорость газа вдоль сопла монотонно растёт, а давление и температура падают. При этом в сопле Лаваля, как и в суживающемся сопле, при отсутствии трения и теплообмена со стенками температура и давление заторможенного потока будут постоянными (Т^* = const, p^* = const) вдоль сопла.

Важной характеристикой сопла Лаваля является относительная площадь выходного сечения (геометрическая степень расширения) сопла

.

Из уравнения неразрывности, записанного для критического и выходного сечений, следует:

. (8.58)

Аналогично для произвольного сечения сопла с площадью F можно записать

. (8.59)

При заданной величине показателя адиабаты k существует однозначная связь (см. вопрос 8.8) между относительной плотностью тока q (λ) и остальными газодинамическими функциями М, λ, τ(λ), π(λ), ε(λ), определяющими при заданных значениях и параметры потока в рассматриваемом произвольном сечении сопла. Таким образом, если известен закон профилирования сопла Лаваля, т. е. изменение площади проходных сечений по длине сопла, то это позволяет определить изменение относительной плотности тока q(λ) и остальных газодинамических функций, а соответственно и всех параметров потока, вдоль сопла.

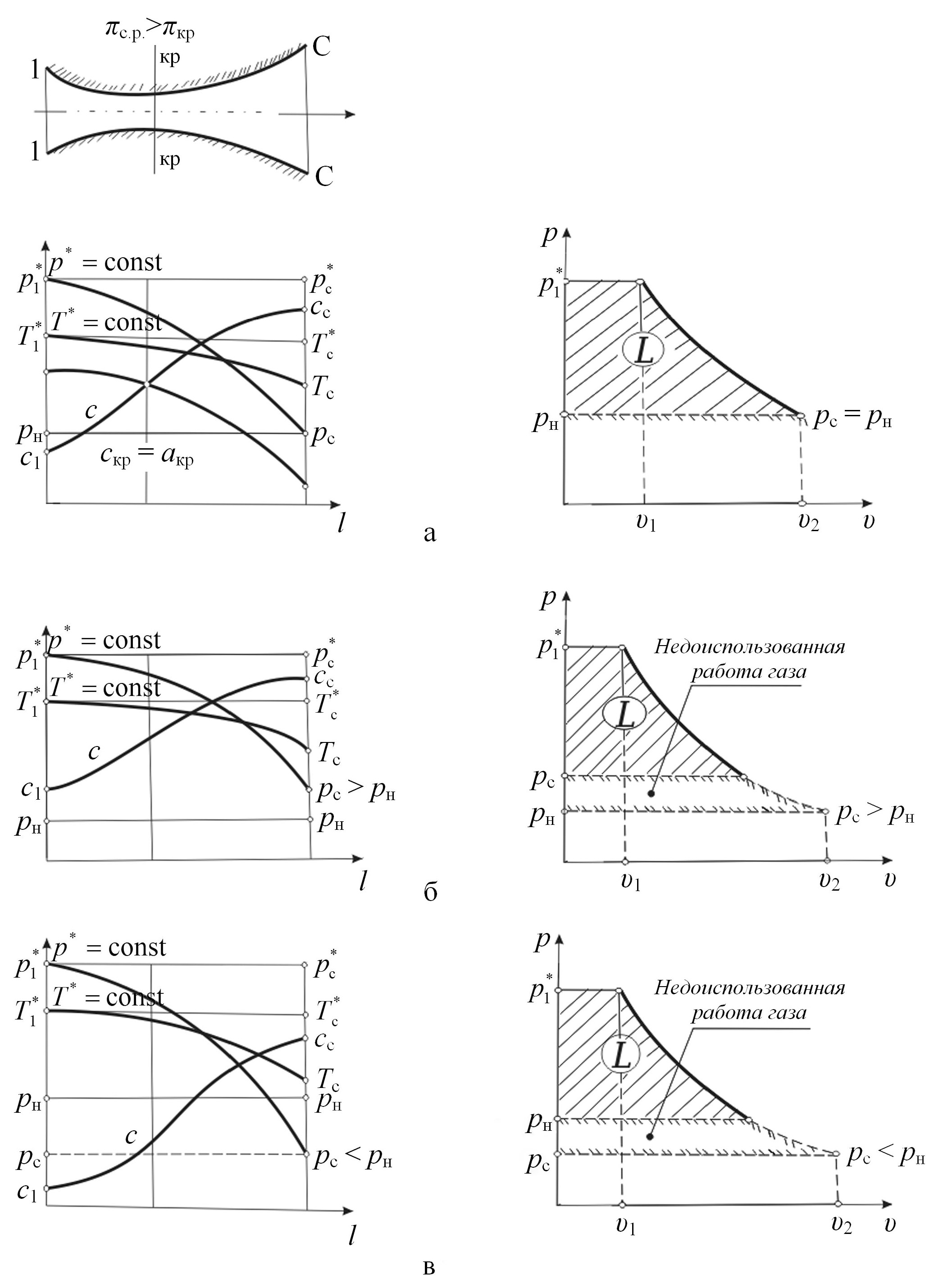
Рис. 8.15. Режимы течения в сверхзвуковом сопле: а – расчётный режим, б – режим с недорасширением, в – режим с перерасширением

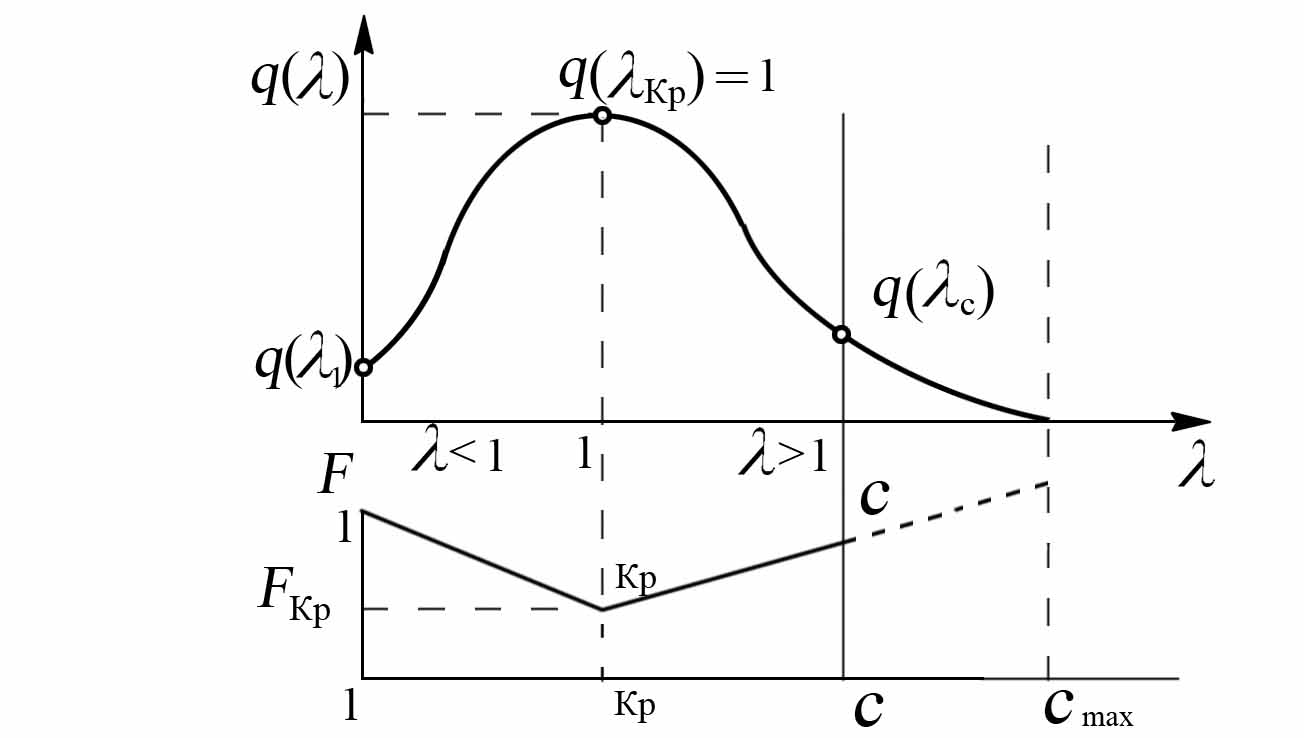
Рис. 8.16. Характер изменения q(λ) в сопле Лаваля

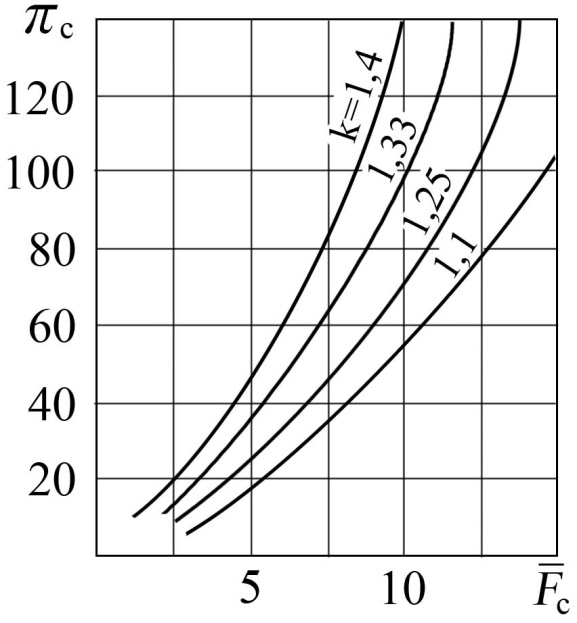
Рис. 8.17. Зависимость = f (π_c)