8.2. Параметры заторможенного потока

Для решения практических задач с помощью уравнения сохранения энергии должны быть известны параметры состояния движущегося газа.

Замер Т и p в движущемся газе значительно сложнее, чем в неподвижном. Это объясняется тем, что измерительные приборы под воздействием набегающего потока показывают завышенные значения. Чтобы устранить этот недостаток, надо сделать так, чтобы измерительные приборы двигались со скоростью равной скорости потока, в этом случае замеренные параметры называются статическими. Но такой способ замера параметров в проточной части осуществить невозможно.

Используя уравнение сохранения энергии, можно найти другие параметры, которые практически просто позволяют определить параметры движущегося потока. Эти параметры названы полными параметрами или параметрами заторможенного потока и обозначаются такими буквами, как и статические, но со звездочкой: p^*, Т^*, ρ^*, i^*. При полном адиабатном торможении газового потока (до нулевой скорости) его кинетическая энергия полностью преображается в тепловую энергию хаотического движения молекул.

Таким образом, параметры заторможенного потока – это параметры газа при его полном адиабатном торможении до нулевой скорости.

П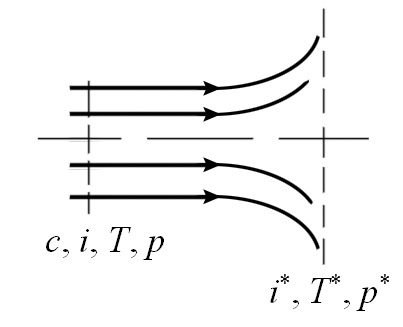 усть в некотором сечении газового потока (рис. 8.3.) скорость, энтальпия, температура и давление равны: с, i, Т, p.

Рис. 8.3. К выводу формул параметров заторможенного потока

Затормозим условно поток с этими параметрами, считая, что теплообмен с окружающей средой отсутствует, т.е. торможение происходит адиабатно. Параметры адиабатно заторможенного потока обозначим так: i^*, Т^*, p^*. Величины i^*, Т^* и p^* называются соответственно: полная энтальпия, полная температура, полное давление.

Поскольку в рассматриваемом случае Q_внеш = 0, L_внеш = 0, то считая с^* = 0, найдем из (7.10) или (7.17) полную энтальпию:

. (8.6)

Уравнение (8.6) перепишем в виде

. (8.6')

Теперь из уравнения (8.6') определим полную температуру

. (8.7)

Давление заторможенного потока найдется из уравнения адиабатного процесса (3.39)

(8.8)

или с учётом (8.7)

. (8.9)

^{Выразим величины Т*, p*, ρ* через число Маха , где а скорость звука.}

^{Учитывая, что} , из (8.7) найдем

.

Поскольку в идеальном газе

k·R·T = a²,

то полная температура через число Маха определяется по формуле:

. (8.10)

Из данного уравнения видно, что полная температура Т^* будет существенно отличаться от статической температуры Т при М > 1.

Давление и плотность заторможенного потока можно легко найти, используя формулы соотношения параметров в адиабатном процессе (3.39), (3.41).

(8.11)

(8.12)

Пример: так для воздуха k = 1,4; при Т = 300 К и М = 5, Т^* = 1800 К. При столь высоких температурах ухудшаются прочностные свойства материалов, из которых выполнены конструкции современных ЛА и АД.