6.9. Скачки уплотнения и их особенности

Скачки уплотнения могут быть прямые и косые. Прямым скачком уплотнения называют такой скачок, поверхность которого перпендикулярна направлению набегающего потока (рис. 6.11,а). Если поверхность скачка наклонена по отношению к направлению набегающего потока, такой скачок уплотнения называют косым (рис. 6.11,б).

Прямые скачки уплотнения возникают перед телом, имеющим тупую закругленную переднюю кромку (рис. 6.12,а), или перед конусом (клином) с большим углом при вершине при движении со сверхзвуковой скоростью. Если сверхзвуковой поток обтекает конус (клин), имеющий малый угол при вершине, возникают косые скачки, начинающиеся от носка тела (рис. 6.12,б,в).

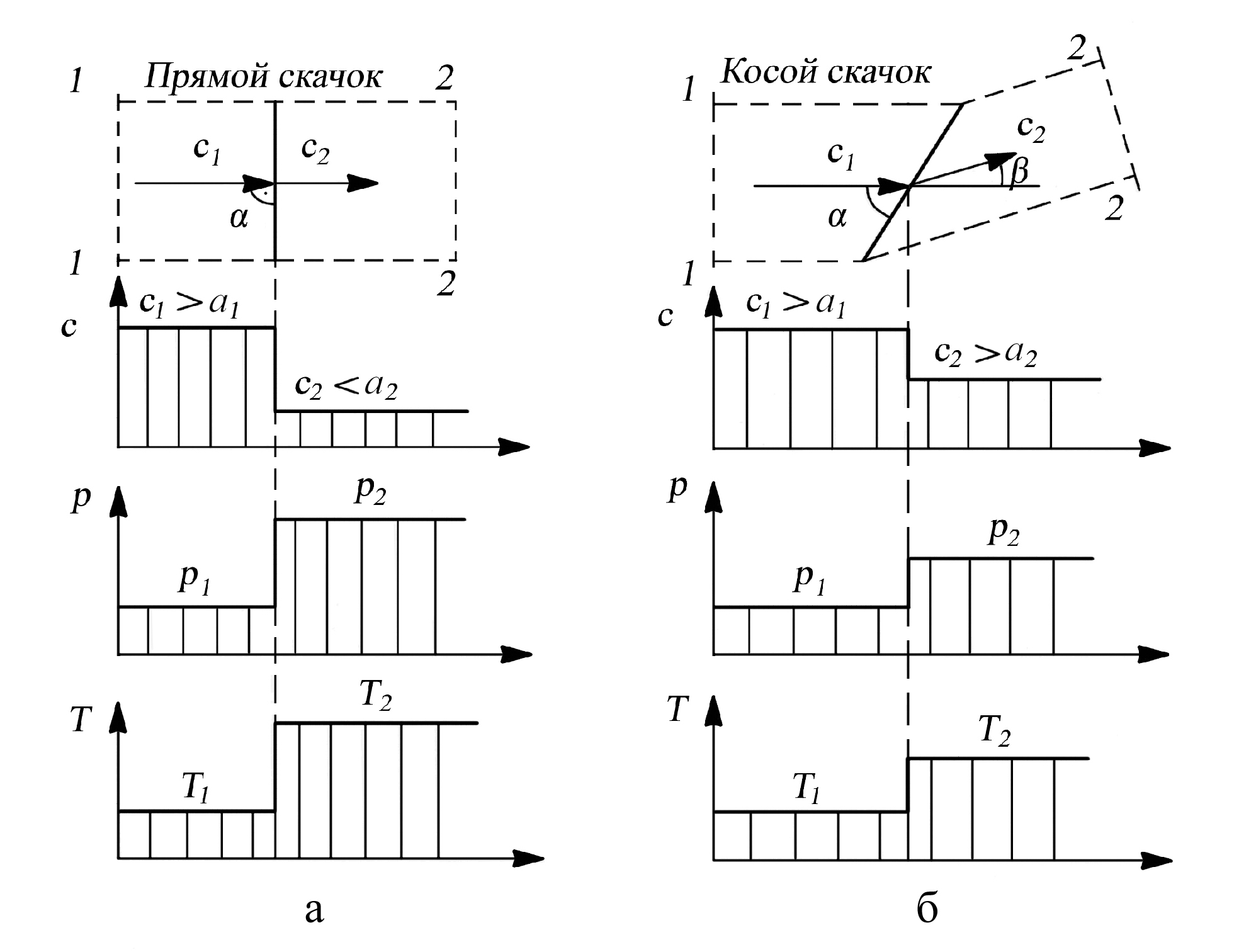
Рис. 6.11. Изменение параметров потока в прямом (а) и

косом (б) скачках уплотнения

Если скачок уплотнения начинается непосредственно на передней поверхности тела, то скачок называется присоединенным. Такие скачки возникают только на достаточно заостренных передних кромках (рис. 6.12,б,в). Если же передняя кромка предмета имеет тупой угол или закругление, то скачок уплотнения располагается на некотором расстоянии от тела; в этом случае скачок называется отсоединенным, или отошедшим (рис. 6.12, а).

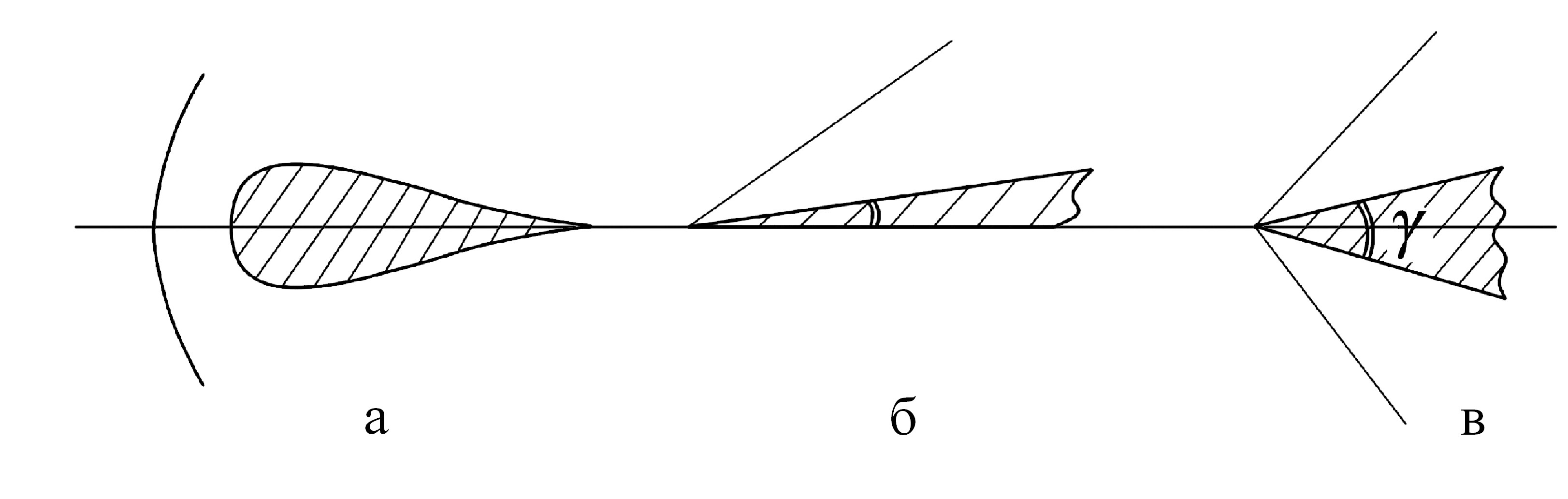
Рис. 6.12. Формы и схемы расположения скачков уплотнения

Интенсивность скачка уплотнения и его вид (прямой или косой) зависят от скорости набегающего потока формы обтекаемого тела. Чем интенсивнее скачок, тем в большей степени происходит снижение скорости за ним, а также увеличение давления и температуры потока. Наиболее интенсивным является прямой скачок, причём с ростом скорости его интенсивность возрастает. За ним скорость потока всегда становится дозвуковой и направление движения потока не изменяется. Скорость c₁ перед прямым скачком и скорость за прямым скачком c₂ связаны между собой следующей зависимостью:

c₁ · c₂ = , (6.13)

где c_кр – критическая скорость.

То есть чем больше скорость c₁ до скачка, тем меньше скорость c₂ после скачка. Скорость за прямым скачком максимально может уменьшаться в шесть раз (c_1max /c_2min = 6). Косой скачок менее интенсивен, чем прямой. За ним поток изменяет направление движения и может быть дозвуковым или сверхзвуковым в зависимости от угла его наклона, который в свою очередь зависит от скорости потока и формы тела. Если угол наклона скачка не намного меньше 90°, он имеет большую интенсивность и поток за ним становится дозвуковым. При уменьшении угла наклона интенсивность скачка снижается, а при некотором его значении скорость за скачком, хотя и уменьшается, остается дозвуковой.

На рис. 6.13. представлена картина, объясняющая изменение направления движения потока за косым скачком.

Скорость потока перед скачком c₁ можно представить как геометрическую сумму двух скоростей:

c_1n = c₁·sinα – нормальная составляющая скорости потока до скачка;

c_1τ = c₁·cosα – тангенциальная составляющая скорости потока до скачка.

После косого скачка тангенциальная составляющая остается неизменной и она равна c_1τ = c_2τ. А для c_1n скачок будет прямым, поэтому нормально составляющая скорости c_2n будет всегда дозвуковой (c_2n < c_1n).

Г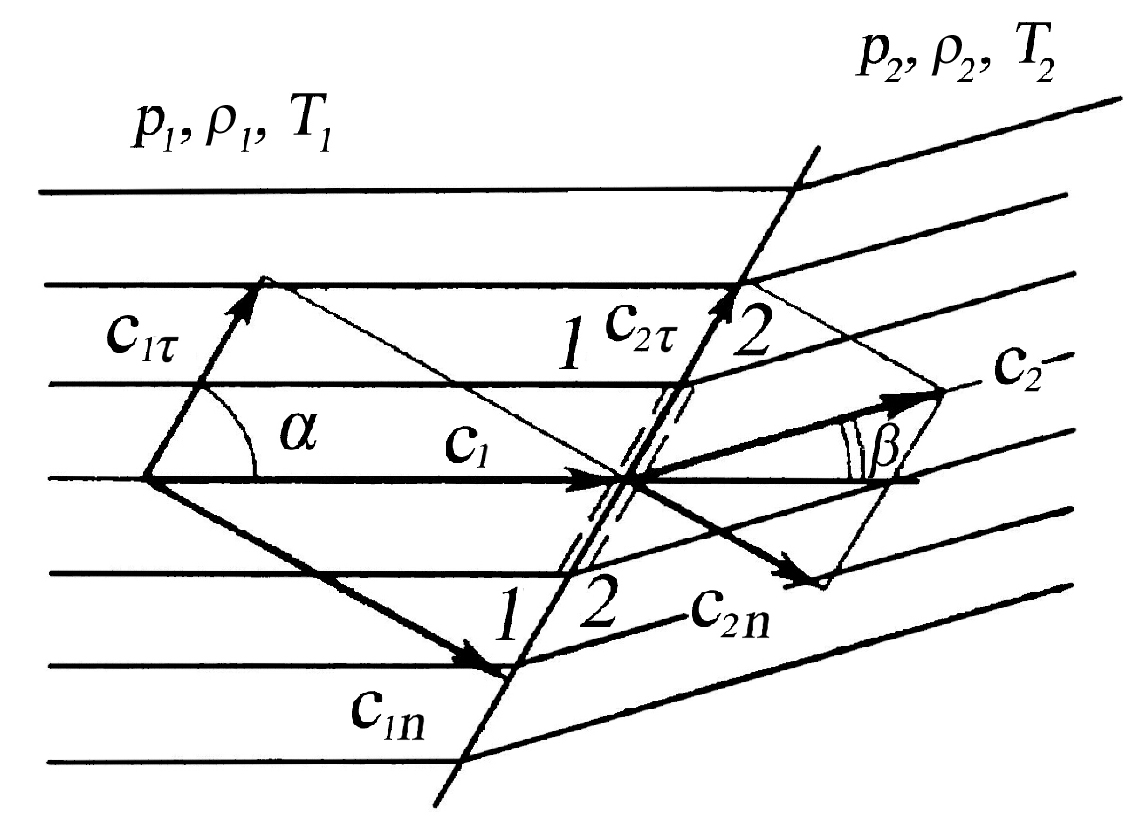 еометрическая сумма двух составляющих c_1n и c_2n дает результирующую скорость потока c₂ после косого скачка, которая поворачивается на некоторый угол β по сравнению с первоначальным направлением.

Рис. 6.13. Изменение направления

потока за косым скачком

Существуют предельные значения заострения тела, при которых возможно образование косых скачков уплотнения. Эти предельные значения зависят от скорости потока перед телом. Так, например, при М = 3 γ_пред = 34° (рис. 6.12,в). Это означает, что при сверхзвуковом обтекании клина с углом при вершине γ > γ_пред, возникает не косой скачок, а скачок уплотнения с криволинейным фронтом (головная ударная волна), поверхность которого не соприкасается с носиком тела.

При прохождении потоком скачка происходит качественное изменение его энергии: часть механической энергии преобразуется в тепловую (внутреннюю). Полная энергия потока до и после скачка не изменяется, однако за скачком поток имеет меньшую механическую энергию и большую тепловую (внутреннюю) энергию, поэтому его работоспособность снижается.

Вследствие преобразования энергии давления в теплоту при прохождении воздуха через скачок уплотнения, полное давление за скачком получается меньше, чем перед скачком.

Полным давлением называется давление адиабатно заторможенного потока. Оно является наибольшим возможным давлением при уменьшении скорости потока до нуля. Вследствие рассеяния энергии при прохождении воздуха через скачок уплотнения полное давление за скачком получается меньше, чем перед скачком. Потери полного давления в скачках уплотнений оцениваются коэффициентом восстановления полного давления σ_ск, который равен отношению полного давления за скачком к полному давлению перед скачком:

. (6.14)

С ростом числа М полёта потери полного давления на скачке возрастают, следовательно, σ_ск уменьшается.

На рис. 6.14. показана схема организации торможения сверхзвукового потока в прямом скачке (рис. 6.14,а) и в системе косых скачков (рис. 6.14,б), при обтекании воздухом гондолы двигателя. Потери полного давления в косом скачке всегда меньше, чем в прямом, поэтому для снижения потерь энергии торможение потока необходимо осуществлять в системе косых скачков (рис. 6.14,б).

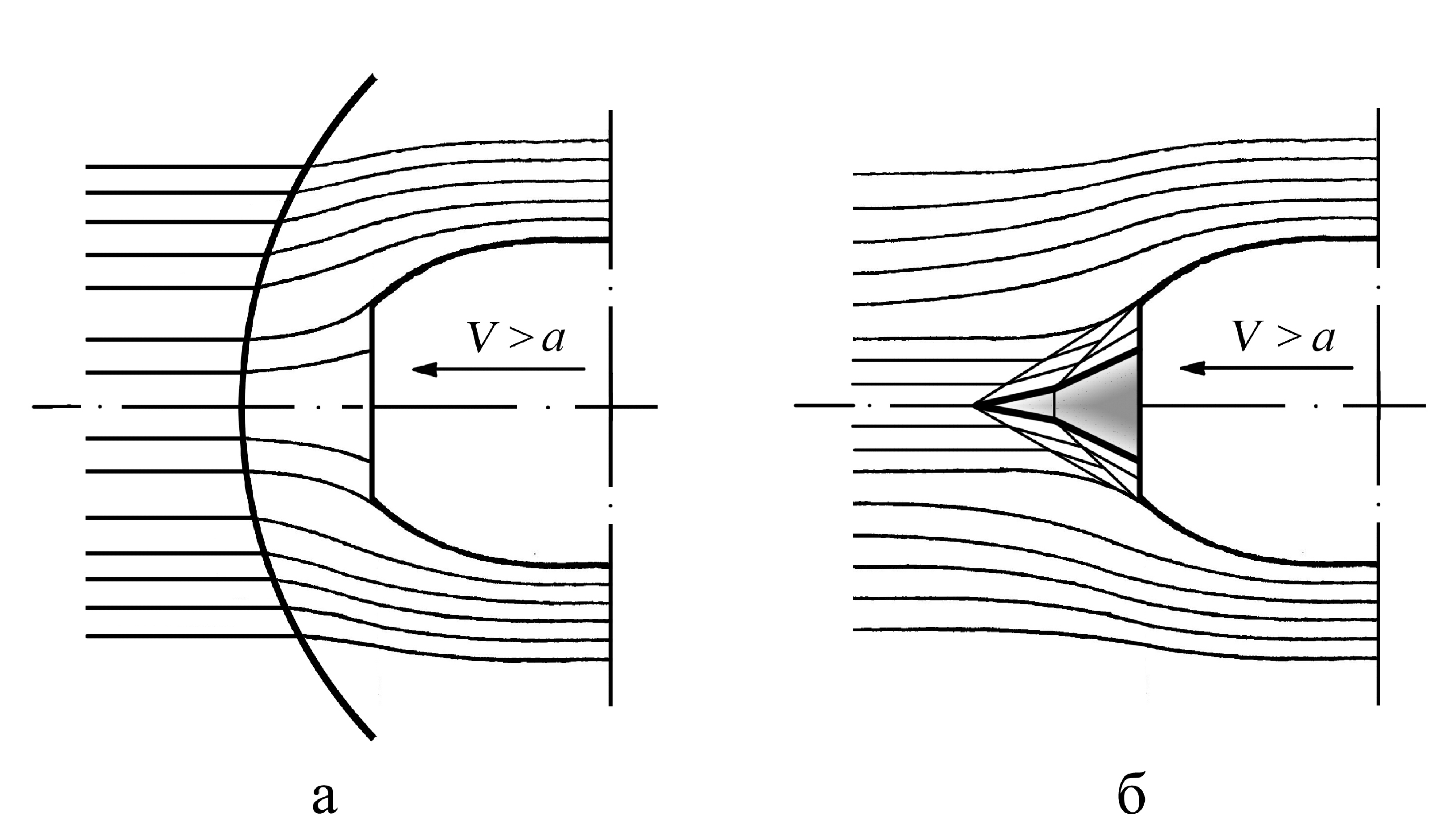
Рис. 6.14. Обтекание воздухом гондолы двигателя при полёте самолёта со сверхзвуковой скоростью: а – дозвуковое входное устройство, б – сверхзвуковое входное устройство

Из рассмотренных выше случаев обтекания сверхзвуковым потоком различных тел можно установить следующие характерные особенности сверхзвукового потока:

- ускорение сверхзвукового потока происходит в расширяющемся канале;

- слабые возмущения в сверхзвуковом потоке охватывают лишь часть пространства внутри конуса малых возмущений, малые возмущения не могут распространяться против сверхзвукового потока;

- если в дозвуковом потоке изменение скорости и параметров потока происходит ещё до встречи с препятствием, то в сверхзвуковом потоке, это точно известно, в скачке уплотнения;

- торможение сверхзвукового потока происходит не постепенно, а скачком. Невозможность предварительной перестройки, подготовки потока при подходе к препятствию является главной особенностью сверхзвукового потока.