Значения коэффициентов δH и δF
Вид зубьев |
δH |
δF |
|
HB1(2)≤350 |
HB1(2)>350 |
||
Простые без модификации* |
0,06 |
0,14 |
0,16 |
Простые с модификацией* |
0,04 |
0,10 |
0,11 |
Косые |
0,02 |
0,04 |
0,06 |
Примечание. * – модификация – снятие фаски на верхней части головки зуба величиной примерно 0,01 и длиной 0,4 модуля для более плавного входа зубьев в зацепление;
Таблица 4.3
Значения коэффициентов g0
Модуль m, мм |
Степень точности |
|||
6 |
7 |
8 |
9 |
|
g0 |
||||
≤3,55 |
3,8 |
4,7 |
5,6 |
7,3 |
≤10 |
4,2 |
5,3 |
5,3 |
8,2 |
>10 |
4,8 |
6,4 |
6,4 |
10,0 |
V – окружная скорость колес, м/с
;
=0,5(dm1+dm2),
мм – условное межосевое расстояние,
определяющее моменты инерции колес.
Удельная расчетная окружная сила в зоне ее наибольшей концентрации, Н/мм
WHtp=Ft KHβ/b.
Коэффициент, учитывающий динамическую нагрузку в зацеплении, KHv=1+(WHv/WHtp).
Удельная расчетная окружная сила, Н/мм.
WHt= Ft KHβ KHv KА/b.
Если полученная величина контактных напряжений σH превышает величину допускаемых контактных напряжений [σH] более чем на 5%, то изменяется ширина венца колес b с последующим пересчетом параметров передачи.
4.4. Проверочный расчет зубьев по усталостным напряжениям изгиба
Расчетные напряжения изгиба зуба (МПа) должны удовлетворять условию
σF1(2)=YF1(2) Yβ Yε WFt/(0,85mm)≤[σF1(2)],
где
– коэффициент, учитывающий форму зуба.
Определяется по графику (рис. 3.3) в
зависимости от эквивалентного числа
зубьев
(при нулевом смещении используется
кривая, соответствующая Х=0).
Для конических зубчатых колес
;
– коэффициент, учитывающий наклон зуба. Для прямозубых колес = 1.
– коэффициент,
учитывающий перекрытие зубьев, принимается
= 1.
Удельная окружная динамическая сила, Н/мм
WFv=δF
g0
V
где δF – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зуба на динамическую нагрузку (см. табл. 4.2);
Удельная расчетная окружная сила в зоне ее наибольшей концентрации, Н/мм
WFtp=Ft KFβ/b,
где KFβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца (рис. 3.2 в, г – схемы 1, 2).
Коэффициент, учитывающий динамическую нагрузку в зацеплении, KFv=1+(WFv/WFtp).
Удельная расчетная окружная сила при изгибе, Н/мм
WFt=Ft KFβ KFv KА/b.
для прямых зубьев Z1(2)Е=Z1(2)/cos δ1(2);
для косых зубьев Z1(2)Е=Z1(2)/(cos3 β1(2) cos δ1(2)).
Расчет производят для элемента пары «шестерня-колесо», у которого меньшая величина отношения [σF1(2)]/YF1(2).
Коэффициент, учитывающий форму зуба (х1(2)=0) (рис. 3.3).
Если при проверочном расчете окажется, что σF1(2) значительно меньше [σF1(2)], то это допустимо, так как нагрузочная способность большинства зубчатых передач ограничивается контактной прочностью. Если перегрузка превышает 5%, то необходимо увеличить модуль с последующим пересчетом числа зубьев и повторить проверочный расчет передачи на изгиб.
4.5. Проверка прочности зубьев при перегрузках (при случайном увеличении крутящего момента сверх номинального)
Максимальные контактные напряжения, МПа
.
Максимальные напряжения изгиба, МПа
.
4.6. Определение параметров конических зубчатых колес
Расчет параметров конических зубчатых колес представлен в разделе 8.
4.7. Силы в зацеплении конических колес
Усилия в зацеплении прямозубых конических колес (рис. 4.2):
Окружные силы, Н
; 
.
Радиальные силы, Н
; 
.
Осевые силы, Н:
; 
.
Здесь α=20˚.
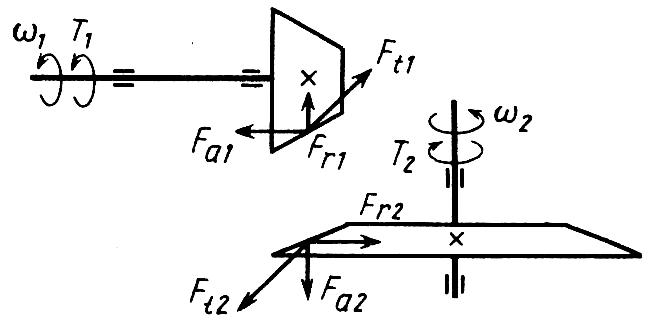
Рис. 4.2. Силы в зацеплении конических передач
4.8. Проектный расчет конической открытой передачи
Исходные данные, выбор материала и расчет допускаемых напряжений выполняют аналогично закрытым передачам (п.п. 4.1 и 4.2)
Расчетный средний модуль зацепления определяется по усталостному напряжению изгиба зуба по формуле:
(4.5)
где km=14;
Z1 – число зубьев шестерни, обычно принимают Z1=15–17;
Z2=Z1U – целое число.
ψbd – коэффициент ширины зубчатого венца шестерни относительно ее диаметра ψbd=b/d′m1=0,3÷0,6;
KFβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца (см. рис. 3.2 в, г – схемы 1, 2);
KHV – коэффициент внешней динамической нагрузки (см. табл. 3.3).
Действительное передаточное число – U=Z2/Z1.
Угол делительного конуса шестерни и колеса, град
δ1 = arctg(Z1/Z2); δ2 = arctg(Z2/Z1).
Эквивалентное число зубьев Z(2)eq=Z1(2)/cos δ1(2).
YF – коэффициент, учитывающий форму зуба, (x1(2)=0, см. рис.3.3).
Расчет производят для элемента пары «шестерня-колесо», у которого меньшая величина отношения [σF1(2)]/YF1(2).
Ширина венца зубчатых колес, мм b =ψbd m′mz1.
Величина b округляется до целых чисел, мм.
Внешнее конусное расстояние, мм
R′e=0,5(m′mZ1/sin δ′1+b) (b/R′e≤0,3).
Наружный модуль, мм m′te= m′m R′e /(R′e-0,5b).
m′te округляют до ближайшего стандартного значения mte=mn, мм (см. табл. 3.5).
Действительное внешнее конусное расстояние, мм
Re=0,5mte
Средний модуль зацепления, мм
mm=mte(Re-0,5b)/Re.
Средний делительный диаметр
шестерни dm1= mmZ1;
колеса dm2= mmZ2.